后缀表达式
不包含括号，运算符放在两个运算对象的后面，所有的计算按运算符出现的顺序，严格从左向右进行（不再考虑运算符的优先规则，如：(2 + 1) * 3 ， 即2 1 + 3 *
编辑本段表达式的计算
运用后缀表达式进行计算的具体做法：
建立一个栈S 。从左到右读后缀表达式，如果读到操作数就将它压入栈S中，如果读到n元运算符(即需要参数个数为n的运算符)则取出由栈顶向下的n项按操作符运算，再将运算的结果代替原栈顶的n项，压入栈S中 。如果后缀表达式未读完，则重复上面过程，最后输出栈顶的数值则为结束。
编辑本段表达式之间的转换
计算机实现转换：
将中缀表达式转换为后缀表达式的算法思想：
·开始扫描；
·数字时，加入后缀表达式；
·运算符：
a. 若为 '('，入栈；
b. 若为 ')'，则依次把栈中的的运算符加入后缀表达式中，直到出现'('，从栈中删除'(' ；
c.剩下的运算符中， 若其优先级高于其它所有的运算符，直接入栈。否则从栈顶开始，依次弹出比当前处理的运算符优先级高和优先级相等的运算符，直到一个比它优先级低的或者遇到了一个左括号就停止。
·当扫描的中缀表达式结束时，栈中的的所有运算符出栈；
人工实现转换
这里我给出一个中缀表达式：a+b*c-(d+e)
第一步：按照运算符的优先级对所有的运算单位加括号：式子变成了：((a+(b*c))-(d+e))
第二步：转换前缀与后缀表达式
前缀：把运算符号移动到对应的括号前面
则变成了：-( +(a *(bc)) +(de))
把括号去掉：-+a*bc+de 前缀式子出现
后缀：把运算符号移动到对应的括号后面
则变成了：((a(bc)* )+ (de)+ )-
把括号去掉：abc*+de+- 后缀式子出现
发现没有，前缀式，后缀式是不需要用括号来进行优先级的确定的。如表达式：3+(2-5)*6/3
后缀表达式 栈
3_________________+
3 ________________+(
3 2 _______________+(-
3 2 5 -_____________ +
3 2 5 - _____________+*
3 2 5 - 6 * ___________+/
3 2 5 - 6 *3 __________+/
3 2 5 - 6 *3 /+________
("_____"用于隔开后缀表达式与栈)
另外一个人认为正确的转换方法:
遍历中缀表达式的每个节点，如果：
1、 该节点为操作数：
直接拷贝进入后缀表达式
2、 该节点是运算符，分以下几种情况：
A、 为“（”运算符：
压入临时堆栈中
B、 为“）”运算符：
不断地弹出临时堆栈顶部运算符直到顶部的运算符是“（”为止。并把弹出的运算符都添加到后缀表达式中
C、 为其他运算符，有以下步骤进行：
比较该运算符与临时栈栈顶指针的运算符的优先级，如果临时栈栈顶指针的优先级高于该运算符的优先级，弹出并添加到后缀表达式中，反复执行前面的比较工作，直到遇到一个栈顶指针的优先级低于或等于该运算符的优先级，停止弹出添加并把该运算符压入栈中。
此时的比较过程如果出现栈顶的指针为‘（’，则停止循环并把该运算符压入栈中，注意：‘（’不要弹出来。
遍历完中缀表达式之后，检查临时栈，如果还有运算符，则全部弹出，并添加到后缀表达式中。
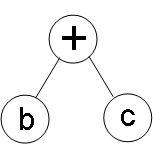
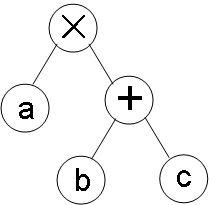
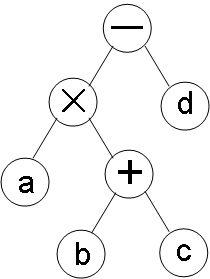
前/中/后缀表达式的转换
