函数的零点相关

前言

涉及到函数的零点和极值点的问题，与转化划归思想、数形结合思想有着紧密的联系。

• 函数\(y=f(x)\)有\(n\)个零点 \(\Longleftrightarrow\) 方程\(f(x)=0\)有\(n\)个不同的根 \(\Longleftrightarrow\) 两个函数图像\(y=f(x)\)与\(y=0\)有\(n\)个不同的交点，思想方法：数形结合。
• 函数\(y=f(x)\)有\(n\)个极值点 \(\Longleftrightarrow\) 函数\(y=f'(x)\)有\(n\)个不同的零点(变号零点) \(\Longleftrightarrow\) 两个函数图像\(y=f'(x)\)与\(y=0\)有\(n\)个不同的穿根交点而不是相切点，思想方法：数形结合。

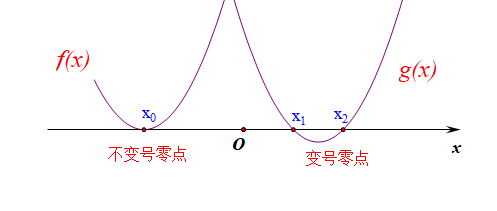
相关延申阅读：零点和极值点

函数的零点问题，是函数与导数章节中非常常见的一类题目，比如已知函数零点个数，求参数的取值范围等，考查的角度非常开阔，对于数学素养要求比较高，在转化与化归上非常灵活，要求我们要好好体会。

典例剖析

已知零点个数

已知函数\(f(x)=x^2+ax+1(a>0)\)，

(1).若\(f(x)\)的值域为\([0,+\infty)\)，求关于\(x\)的方程\(f(x)=4\)的解；

分析：题目已知\(f(x)\)的值域为\([0,+\infty)\)，其本质是为了告诉\(a\)的取值；

只有函数\(f(x)\)和\(x\)轴相切时，\(f(x)\)的值域才能为\([0,+\infty)\)，

故\(\Delta =a^2-4=0\)，解得\(a=2\)(舍去负值)，则需要求解方程\(x^2+2x+1=4\)

即求解\(x^2+2x-3=0\)，解得\(x=-3\)或\(x=1\)，故其解集为\(\{-3,1\}\)。

(2).当\(a=2\)时，函数\(g(x)=[f(x)]^2-2m\cdot f(x)+m^2-1\)在\([-2，1]\)上有三个零点，求\(m\)的取值范围；

分析：函数\(g(x)\)的零点，即方程\([f(x)]^2-2m\cdot f(x)+m^2-1=0\)的根，

而方程可以分解为\([f(x)-(m-1)][f(x)-(m+1)]=0\)，

故方程\(f(x)=m-1\)和方程\(f(x)=m+1\)在\(x\in [-2，1]\)上共有三个解；

在同一个坐标系中做出函数\(y=f(x)(x\in [-2，1])\)和直线\(y=m-1\)和\(y=m+1\)，如图所示，

当\(0<m-1\leqslant 1\)时，函数\(y=f(x)\)与直线\(y=m-1\)有两个交点；

同时\(m+1\in [2，3]\)，此时函数\(y=f(x)\)与直线\(y=m+1\)只有一个交点，满足题意；

故只需要由\(0<m-1\leqslant 1\)，解得\(m\in (1，2]\).

【2017\(\cdot\) 西安模拟】已知函数\(f(x)=kx^2-lnx\)有两个零点，求参数\(k\)的取值范围【\(\qquad\)】

$A.k > \cfrac{e}{2}$ $B.0< k <\sqrt{e}$ $C.k > \cfrac{\sqrt{2}e}{2}$ $D.0< k <\cfrac{1}{2e}$

【法1】：不完全分离参数法，数形结合法，定义域为\((0，+\infty)\)，转化为方程\(kx^2=lnx\)有两个不同的实数根，

再转化为函数\(y=kx^2\)与函数\(y=lnx\)的图像有两个不同的交点，

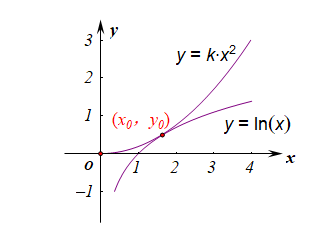
如图设两个函数的图像相切于点为\((x_0，y_0)\)，

则有关系式\(\begin{cases}2kx_0=\cfrac{1}{x_0}\\kx_0^2=y_0\\y_0=lnx_0\end{cases}\)，

解得\(y_0=\cfrac{1}{2}，x_0=\sqrt{e}\)，即切点为\((\sqrt{e}，\cfrac{1}{2})\)，

再代入函数\(y=kx^2\)，求得此时的\(k=\cfrac{1}{2e}\)，

再结合函数\(y=kx^2\)的系数\(k\)的作用，可得两个函数要有两个不同的交点，

则\(k\in(0，\cfrac{1}{2e})\)。 故选\(D\).

【法2】：完全分离参数法，定义域为\((0，+\infty)\)，转化为方程\(kx^2=lnx\)有两个不同的实数根，

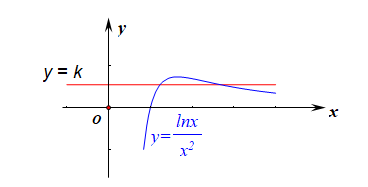
再转化为\(k=\cfrac{lnx}{x^2}\)有两个不同的实数根，

再转化为函数\(y=k\)和函数\(y=g(x)=\cfrac{lnx}{x^2}\)的图像有两个不同的交点，

用导数研究函数\(g(x)\)的单调性，\(g'(x)=\cfrac{\cfrac{1}{x}\cdot x^2-lnx\cdot 2x}{(x^2)^2}=\cfrac{1-2lnx}{x^3}\)，

令\(1-2lnx>0\)，得到\(0< x<\sqrt{e}\)，令\(1-2lnx<0\)，得到\(x >\sqrt{e}\)，

即函数\(g(x)\)在区间\((0，\sqrt{e}]\)上单调递增，在\([\sqrt{e}，+\infty)\)上单调递减，

故\(g(x)_{max}=g(\sqrt{e})=\cfrac{1}{2e}\)，

作出函数\(g(x)\)和函数\(y=k\)的简图，由图像可得\(k\)的取值范围是\(k\in(0，\cfrac{1}{2e})\)。 故选\(D\).

【姊妹题2】函数\(f(x)=(x-2)e^x+a(x-1)^2\)有两个零点，求\(a\)的取值范围。

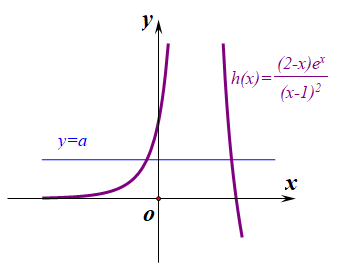
【法1】：方程\(a(x-1)^2=(2-x)e^x\)有两个不同的根，

即函数\(g(x)=a(x-1)^2\)与函数\(h(x)=(2-x)e^x\)有两个不同的交点，

其中函数\(h(x)=(2-x)e^x\)的图像需要先判断单调性，

用导数求得\(x\in(-\infty，1)\)上单调递增，在\(x\in(1，+\infty)\)上单调递减，

作图时需要注意这样几点，\(x<1\)时，\(h(x)>0\)，\(h(1)=e\)，\(h(2)=0\)；

做出如右图所示的图像，

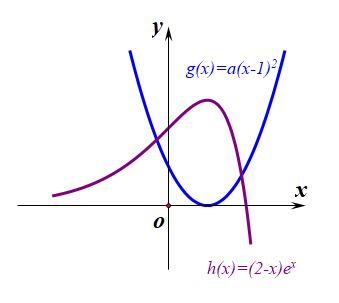
由图像可得，\(a\)的取值范围是 \(a >0\)；即\(a\in(0，+\infty)\)；

【法2】：分离参数得到，\(a=\cfrac{(2-x)e^x}{(x-1)^2}\)

同样可以做，只是做函数\(h(x)=\cfrac{(2-x)e^x}{(x-1)^2}\)的图像比较难，

用导数求得函数\(h(x)\)在\((-\infty，1)\)上单调递增，在\((1，+\infty)\)上单调递减，

注意\(x<1\)时，\(h(x)>0\)，\(h(0)=2\)，\(h(2)=0\)，且\(x=1\)是其渐近线；如右图所示；

故\(a\)的取值范围是 \(a >0\)；即\(a\in(0，+\infty)\)；

解后反思：

1、法1要求我们对函数\(y=kx^2\)的系数的\(k\)的几何意义要很清楚。

2、合理的转化划归是学习数学的一个必备素养。

3、图是高中数学的生命线。

4、这几个题目的求解也可以使用上述的两个思路，如出一辙，这也让我们感受到数学的学习中，真的有必要总结一些比较特殊的模型，以简化思维，节省时间。

【2017•潍坊模拟】已知函数\(f(x)=\cfrac{1}{3}x^3－bx^2＋c(b，c为常数)\)，当\(x＝2\)时，函数\(f(x)\)取得极值，若函数\(f(x)\)只有三个零点，则实数\(c\)的取值范围是________．

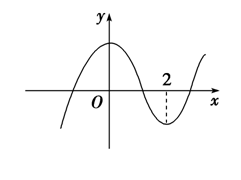
分析：\(f'(x)=x^2-2bx\)，由\(f'(2)=0\)得到\(b=1\)，故\(f'(x)=x^2-2x=x(x-2)\)，

故函数\(f(x)\)在\((-\infty，0)\)上\(\nearrow\)，在\((0，2)\)上\(\searrow\)，在\((2，+\infty)\)上\(\nearrow\)；

要使得函数\(f(x)\)只有三个零点，则只需且必须\(\begin{cases}f(0)=c>0\\f(2)=\cfrac{8}{3}-4+c<0\end{cases}\)，

解得\(c\in(0，\cfrac{4}{3})\)。

引申：1、如果是仅仅只有一个零点呢？2、如果有两个零点呢？

【2016\(\cdot\)山东卷】已知函数\(f(x)=\begin{cases}|x|，x<m\\x^2-2mx+4m，x\ge m\end{cases}\)，其中\(m>0\)，若存在实数\(b\)，使得关于\(x\)的方程\(f(x)=b\)有三个不同的根【等价题目】已知函数\(f(x)=\begin{cases}|x|，x<m\\x^2-2mx+4m，x\ge m\end{cases}\)，其中\(m>0\)，若存在实数\(b\)，使得函数\(y=f(x)-b\)有三个不同的零点，则\(m\)的取值范围是_____________。，则\(m\)的取值范围是_____________。

分析：由于\(m>0\)，故在\(x\)轴的正半轴任取一点记为\(m\)，做出分段函数\(f(x)\)的两段函数图像，

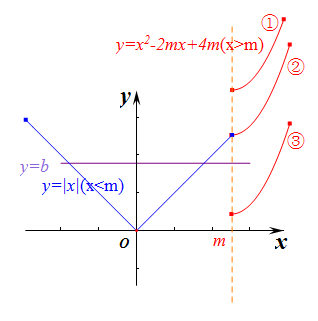
注意第二段函数\(y=x^2-2mx+4m=(x-m)^2+4m-m^2\)，对称轴是\(x=m\)，最小值是\(4m-m^2\)，

由于最小值随\(m\)是变化的，故做出了三种情形，编号为①②③；

要使得关于\(x\)的方程\(f(x)=b\)有三个不同的根，

则需要函数\(y=f(x)\)与函数\(y=b\)的图像有三个不同的交点，

很显然，图①②都不满足题意，只有图③满足题意，

然后将图形语言转化为数学语言即可，

即\(|m|>m^2-2m^2+4m\)，由\(m>0\)，

得到\(m^2-3m>0\)，解得\(m<0\)或\(m>3\)

又\(m>0\)，综上\(m>3\)。\(m\in (3，+\infty)\)。

已知函数\(f(x)\)是R上的偶函数，且对任意的\(x\in R\)都有\(f(x+2)=f(x)\)成立，当\(0\leq x\leq 1\)时，\(f(x)=x^2\)，若函数\(y=x+a\)与函数\(y=f(x)\)的图像在\([0，2]\)上恰有两个不同的公共点，则\(a\)的取值范围是__________。

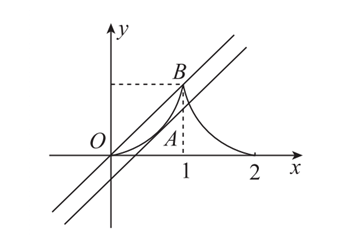
分析：由于对任意的\(x\in R\)都有\(f(x+2)=f(x)\)成立，则\(T=2\)，

又因为当\(0\leq x\leq 1\)时，\(f(x)=x^2\)，

故只做出函数\(f(x)\)在一个周期\([0，2]\)上的图像，如右图所示。

当\(a=0\)时，此时函数\(y=x+a\)经过原点，恰好和\(y=f(x)\)有两个不同的交点，符合题意；

然后我们让直线沿着\(y\)轴向下平移，

发现向下平移一开始，二者有三个不同交点，但当二者相切时，又有了两个交点，

再往下平移，就只有一个交点了。

设切点为\(A(x_0，y_0)\)，则\(f'(x)=2x\)，

由\(f'(x_0)=2x_0=1\)，及\(y_0=x_0^2\)，

解得\(x_0=\cfrac{1}{2}\)，\(y_0=\cfrac{1}{4}\)，代入\(y_0=x_0+a\)，

得到\(a=-\cfrac{1}{4}\)。

故所求\(a\)的取值范围是\(a=0\)或\(a=-\cfrac{1}{4}\)。

解后反思：
1、若题目变成“在区间\([0，1]\)上二者恰有两个不同的交点”，则\(-\cfrac{1}{4}<a\leq 0\)；

2、若题目变成“在区间\([0，2]\)上二者恰有三个不同的交点”，则\(-\cfrac{1}{4}<a< 0\)；

3、若题目变成“在区间\([0，1]\)上二者恰有一个不同的交点”，则\(a=-\cfrac{1}{4}\)；

4、若题目变成“在区间\([0，2]\)上二者恰有一个不同的交点”，则\(-2<a<-\cfrac{1}{4}\)；

【2019届高三理科数学资料用题】已知函数\(f(x)=x^2-|x|+a\)与\(y=1\)有\(4\)个交点，则实数\(a\)的取值范围是_______________。

分析：将函数转化为\(f(x)=|x|^2-|x|+a\)，故\(f(x)\)为偶函数，

重点做\(x\ge 0\)时的函数图像，\(f(x)=x^2-x+a=(x-\cfrac{1}{2})^2+a-\cfrac{1}{4}(x\ge 0)\)，

对称轴为\(x=\cfrac{1}{2}\)，最低点为\((\cfrac{1}{2}，a-\cfrac{1}{4})\)，和\(y\)轴的交点为\((0 ，a)\)，

再完善\(x<0\)时的图像，得到函数\(y=f(x)\)的完整图像，

想一想，当参数\(a\)变化时，\(f(x)\)的图像如何变化？

由图像可知，要使得函数\(f(x)=x^2-|x|+a\)与\(y=1\)有\(4\)个交点，

则必须满足\(a>1\)且\(a-\cfrac{1}{4}<1\)，

解得\(a\in (1，\cfrac{5}{4})\)。

【2019届高三理科数学三轮模拟训练题】已知函数\(f(x)=\left\{\begin{array}{l}{x^3，x\leq a}\\{x^2+2x，x>a}\end{array}\right.\)，若存在实数\(b\)，使得函数\(g(x)=f(x)+b\)有两个零点，则\(a\)的取值范围是【】

$A.(-\infty，-1)\cup(-1，0)\cup(2，+\infty)$

$B.(-\infty，-2)\cup(-1，0)\cup(1，+\infty)$

$C.(-\infty，0)\cup(1，+\infty)$

$D.(-\infty，-1)\cup(2，+\infty)$

法1：分析：本题目需要先做出函数的图像，如下图所示，同时要明白参数\(a\)的作用，

存在实数\(b\)，使得函数\(g(x)=f(x)+b\)有两个零点，意味着直线\(y=-b\)与分段函数\(f(x)\)的两段都有交点，

情形一，两段函数都是单调的，此时需要\(a^2+2a<a^3\)，解得\(a>2\)或者\(-1<a<0\)；

情形二，第二段函数不单调，此时需要\(a<-1\)；

综上所述，\(a\in (-\infty，-1)\cup(-1，0)\cup(2，+\infty)\)，故选\(A\)。

法2：做出分段函数的图像，使用排除法，令\(a=\cfrac{3}{2}\)，和\(a=-\cfrac{1}{2}\)验证，可以排除\(B\)，\(C\)，\(D\)，故选\(A\)。

解后反思：①将题目中的条件“存在实数\(b\)，使得函数\(g(x)=f(x)+b\)有两个零点”更改为函数\(f(x)\)是单调递增的函数，则\(a\)的取值范围为\(\{a\mid a=-1或0\leq a\leq 2\}\)；

②将题目中的条件“存在实数\(b\)，使得函数\(g(x)=f(x)+b\)有两个零点”更改为函数\(f(x)\)不是单调递增的函数，则\(a\)的取值范围为\(\{a\mid a<-1或-1<a<0或 a>2\}\)；

【2019届高三理科数学三轮模拟试题】已知函数\(y=a+2lnx\)与函数\(y=x^2+2\)的图像在\(x\in [\cfrac{1}{e}，e]\)内有两个交点，则实数\(a\)的取值范围是________.

法1：转化为方程\(a=x^2-2lnx+2\)在\(x\in [\cfrac{1}{e}，e]\)内有两个根，

即函数\(y=a\)和函数\(y=g(x)=x^2-2lnx+2\)在\(x\in [\cfrac{1}{e}，e]\)内有两个交点，

\(g'(x)=2x-\cfrac{2}{x}=\cfrac{2(x-1)(x+1)}{x}\)，则在\([\cfrac{1}{e}，1]\)上单调递减，在\([1，e]\)上单调递增，

又\(g(1)=3\)，\(g(\cfrac{1}{e})=4+\cfrac{1}{e^2}\)，\(g(e)=e^2>4+\cfrac{1}{e^2}\)，

做出示意图，可知实数\(a\)的取值范围为\(a\in (3，4+\cfrac{1}{e^2}]\)

法2：由函数\(y=a+2lnx\)与函数\(y=x^2+2\)的图像在\(x\in [\cfrac{1}{e}，e]\)内有两个交点，

则可知函数\(f(x)=2lnx-x^2+a-2\)在\(x\in [\cfrac{1}{e}，e]\)内有两个零点，

\(f'(x)=\cfrac{2}{x}-2x=\cfrac{-2(x^2-1)}{x}=\cfrac{-2(x+1)(x-1)}{x}\)

则当\(x\in [\cfrac{1}{e}，1]\)时，\(f'(x)>0\)，\(f(x)\)单调递增，

当\(x\in [1，e]\)时，\(f'(x)<0\)，\(f(x)\)单调递减，

又由于\(f(1)=2ln1-1+a-2=a-3\)，\(f(\cfrac{1}{e})=2ln\cfrac{1}{e}-\cfrac{1}{e^2}+a-2=-4-\cfrac{1}{e^2}+a\)，

\(f(e)=2lne-e^2+a-2=-e^2+a\)，\(f(\cfrac{1}{e})>f(e)\)，

则要使得函数\(f(x)=2lnx-x^2+a-2\)在\(x\in [\cfrac{1}{e}，e]\)内有两个零点，

必须满足条件\(\left\{\begin{array}{l}{f(1)=a-3>0}\\{f(\cfrac{1}{e})=-\cfrac{1}{e^2}-4+a\leqslant 0}\end{array}\right.\)

解得\(3<a\leqslant \cfrac{1}{e^2}+4\)，即可知实数\(a\)的取值范围为\(a\in (3，4+\cfrac{1}{e^2}]\)

【2018届广东东莞模拟】已知函数\(f(x)\)，任取两个不相等的正数\(x_1\)、\(x_2\)，总有\([f(x_1)-f(x_2)]\)\((x_1\)\(-x_2)\)\(>0\)，对于任意的\(x>0\)，总有\(f[f(x)-lnx]=1\)。若函数\(g(x)\)\(=f'(x)\)\(+f(x)\)\(-m^2+m\)有两个不同的零点，则正实数\(m\)的取值范围是___________。

分析：本题目的难点之一是利用代换法先求得函数\(f(x)\)的解析式；然后再求正实数\(m\)的取值范围。

由于任意不等正数\(x_1\)、\(x_2\)，有\([f(x_1)-f(x_2)](x_1-x_2)>0\)，则\(f(x)\)在\((0，+\infty)\)上单调递增，

令\(f(x)-lnx=t\)，则\(f(t)=1\)①，又由于\(f(x)-lnx=t\)，即\(f(x)=lnx+t\)，令\(x=t\)，则\(f(t)=lnt+t\)②，

由①②可知，\(lnt+t=1\)，即\(lnt=1-t\)，观察可知，\(t=1\)，即函数\(f(x)\)的解析式为\(f(x)=lnx+1\)；

接下来，用常规方法求正实数\(m\)的取值范围。

由题目可知，\(g(x)=lnx+1+\cfrac{1}{x}-m^2+m\)有两个不同的零点，即方程\(lnx+1+\cfrac{1}{x}-m^2+m=0\)有两个不同的根，

整体分离参数得到，\(m^2-m=lnx+1+\cfrac{1}{x}\)，令\(h(x)=lnx+1+\cfrac{1}{x}\)，

则\(h'(x)=\cfrac{x-1}{x^2}\)，则\(x\in (0，1)\)时，\(h'(x)<0\)，\(h(x)\)单调递减，\(x\in (1，+\infty)\)时，\(h'(x)>0\)，\(h(x)\)单调递增，

故\(h(x)_{min}=h(1)=2\)，则题目转化为\(m^2-m>2\)，解得\(m<-1\)或\(m>2\)，又由\(m>0\)，可得\(m>2\)，

即正实数\(m\)的取值范围是\((2，+\infty)\).

求零点个数

函数\(f(x)=\begin{cases}x^3-x-1，&x\ge2或x\leq -1\\1&-1<x<2\end{cases}\)，求函数\(g(x)=f(x)-x\)的零点。

分析：函数\(g(x)\)的零点，即方程\(f(x)=x\)的根，这样问题就转化为分段函数方程了。

再等价转化得到\(\begin{cases}x\ge 2或x\leq -1\\x^3-x-1=x\end{cases}\)或者\(\begin{cases}-1<x<2\\x=1\end{cases}\)，

解第二个不等式组容易得到\(x=1\) ，难点是解第一个不等式组。

由\(x^3-2x-1=0\)，用试商法可得\(x=-1\)是其一个根，

故分解为\(x^3+1-2(x+1)=(x+1)(x^2-x-1)=0\)，解得\(x=-1\)或\(x=\cfrac{1\pm\sqrt{5}}{2}\)(不符舍去)，

故函数\(g(x)=f(x)-x\)的零点为\(x=-1\)和\(x=1\)。

【2019届高三理科数学资料用题】【2018日照一模】已知函数\(f(x)=\left\{\begin{array}{l}{|lgx|，x>0}\\{2^{|x|}，x\leq 0}\end{array}\right.\)，则函数\(y=2f^2(x)-3f(x)+1\)的零点个数是【5】个。

分析：函数\(y=2f^2(x)-3f(x)+1\)的零点个数即方程\(2f^2(x)-3f(x)+1=0\)的根的个数，

故先求解方程\(2f^2(x)-3f(x)+1=0\)，即\([2f(x)-1][f(x)-1]=0\)，

解得\(f(x)=1\)或\(f(x)=\cfrac{1}{2}\)，

接下来原方程的根的个数转化为方程\(f(x)=1\)或\(f(x)=\cfrac{1}{2}\)的根的个数，

故做出函数\(y=f(x)\)的图像和直线\(y=1\)和\(y=\cfrac{1}{2}\)，

由图像可以看出，其共有\(5\)个交点，故原函数的零点个数为\(5\)个。

【学生问题，难】定义在\(R\)上的函数\(f(x)\)满足\(f(x)+f(x+4)=16\)，当\(x\in (0，4]\)时，\(f(x)=x^2-2^x\)；则函数\(f(x)\)在\([-4，2016]\)上的零点个数是【B】

$A、504$ $B、505$ $C、1008$ $D、1009$

分析：由\(f(x)+f(x+4)=16\)，得到\(f(x+4)+f(x+8)=16\)，两式相减得到，

\(f(x+8)=f(x)\)，即\(T=8\)；

当\(x\in (0，4]\)时，\(f(x)=x^2-2^x\)已经知道，关键是求得\(x\in (4，8]\)上的解析式；

当\(0<x\leq 4\)，\(4<x+4\leq 8\)，

故\(f(x+4)=16-f(x)\)，令\(x+4=t\)，则\(x=t-4\)，则\(t\in (4，8]\)

故\(f(t)=16-f(t-4)\)，\(t\in (4，8]\)

即\(f(x)=16-f(x-4)\)，\(x\in (4，8]\)

则周期函数\(f(x)=\left\{\begin{array}{l}{x^2-2^x，0<x\leq 4}\\{16-(x-4)^2-2^{x-4}，4<x\leq 8}\end{array}\right.\)

接下来的难点是做函数\(f(x)\)在一个周期上的图像，

重点是做\(y=x^2-2^x，0<x\leq 4\)的图像。

结合上图可以做出函数\(y=x^2-2^x，0<x\leq 4\)的图像。

再做出\(x\in (4，8]\)时的\(f(x)\)的图像。

在区间\([0，2016]\)上，包含\(\cfrac{2016}{8}=252\)个周期，每个周期上的零点有两个，

故有\(252\times2=504\)个，但是在\([-4，0)\)上还有一个，

故共有\(505\)个零点，故选\(B\)。

零点唯一

若\(f(x)=2x^3-ax^2+1(a\in R)\)，在\((0，+\infty)\)内有且只有一个零点，则\(f(x)\)在\([-1，1]\)上的最大值与最小值的和为______。

分析：方程\(a=\cfrac{2x^3+1}{x^2}=g(x)\)在\((0，+\infty)\)内有且只有一解，

即函数\(y=g(x)\)与\(y=a\)在\((0，+\infty)\)内有且只有一个交点，

用数形结合求得\(a=3\)，然后用常规方法求得最值即可。

【2014高考新课标Ⅰ卷理科，第11题】已知函数\(f(x)=ax^3-3x^2+1\)，若函数\(f(x)\)存在唯一零点 \(x_0\)，且\(x_0>0\)，则\(a\)的取值范围是【C】

$A(2，+\infty)$ $B(1，+\infty)$ $C(-\infty，-2)$ $D(-\infty，-1)$

法1：由于函数\(f(x)\)存在唯一零点 \(x_0\)，且\(x_0>0\)，

则方程\(f(x)=0\)有唯一的正实数解，即\(ax^3-3x^2+1=0\)有唯一的正实数解，

即方程\(a=\cfrac{3x^2-1}{x^3}\)有唯一的正实数解，

即函数\(y=a\)和函数\(y=h(x)=\cfrac{3x^2-1}{x^3}=\cfrac{3}{x}-\cfrac{1}{x^3}(x>0)\)有唯一的交点，

其余思路待补充。

法2：先将题目转化为，方程\(ax^3=3x^2-1\)有唯一的正实数解，

则静态函数\(y=3x^2-1\)和动态函数\(y=ax^3\)只能在区间\((0 ，+\infty)\)上有交点，

此处需要我们知道函数\(y=ax^3\)的参变数\(a\)的作用，

由图像可知，当\(a\leq 0\)时，都不满足题意，故需要\(a<0\)，

但当\(a\)取很小的负值时，显然满足题意，当\(a\)为某一个恰当的负值时，两个曲线在\(x<0\)时可能相切，

当然，此处你可能还会认为是有相切，还有相交，这不要紧，我们通过下述的计算就能回答这个疑惑。

设切点坐标为\(P(x_0，y_0)\)，则有\(x_0<0\)，

则有\(\left\{\begin{array}{l}{3ax_0^2=6x_0}\\{y_0=ax_0^3}\\{y_0=3x_0^2-1}\end{array}\right.\)

解得\(x_0=-1\)，\(y_0=2\)，将切点\(P(-1，2)\)代入\(y=ax^3\)，解得\(a=-2\)，

故当\(a<-2\)时，两条曲线在\(x<0\)上没有交点，只在\(x>0\)上有交点，故满足题意，

即\(a\)的取值范围时\((-\infty，-2)\)，故选\(C\)。

法3：利用导数方法，同时注意题目的隐含条件，\(f(0)=1\)，

\(f'(x)=3ax^2-6x=3x(ax-2)\)，

①当\(a=0\)时，原函数为\(y=-3x^2+1\)，有两个零点，不符合题意，舍去。

②当\(a>0\)时，由导函数的图像可知，函数\(f(x)\)在区间\((-\infty，0)\)上单调递增，在区间\((0，\cfrac{2}{a})\)上单调递减，在区间\((\cfrac{2}{a}，+\infty)\)上单调递增，

此时函数在区间\((-\infty，0)\)上必有一个零点，不符合题意，舍去。

③当\(a<0\)时，由导函数的图像可知，函数\(f(x)\)在区间\((-\infty，\cfrac{2}{a})\)上单调递减，在区间\((\cfrac{2}{a}，0)\)上单调递增，在区间\((0，+\infty)\)上单调递减，

此时只需要函数\(f(x)\)的极小值大于零即可，即\(f(\cfrac{2}{a})>0\)，

即\(a\cdot (\cfrac{2}{a})^3-3\cdot (\cfrac{2}{a})^2+1>0\)，化简得到\(a^2>4\)，

解得\(a<-2\)或\(a>2\)，又\(a<0\)，故\(a<-2\)。

即\(a\)的取值范围时\((-\infty，-2)\)，故选\(C\)。

【2017\(\cdot\)全国卷3理科第12题】已知函数\(f(x)=x^2-2x+a(e^{x-1}+e^{-x+1})\)有唯一的零点，则\(a\)的值为【】

$A.-\cfrac{1}{2}$ $B.\cfrac{1}{3}$ $C.\cfrac{1}{2}$ $D.1$

【法1】：分离常数法，本题目就不适宜使用此法；

由\(f(x)=0\)得到\(a(e^{x-1}+e^{-x+1})=-x^2+2x\)，

分离得到\(a=\cfrac{-x^2+2x}{e^{x-1}+e^{-x+1}}=h(x)\)，

你应该能感觉到函数\(h(x)\)若要用导数分析其单调性，

那会是相当的难，故分离参数的思路一般在这个题目中，就自然舍弃了。

【法2】：由题目可知方程\(f(x)=0\)仅有一解，即\(a(e^{x-1}+e^{-x+1})=-x^2+2x\)仅有一解，

即函数\(y=a(e^{x-1}+e^{-x+1})\)与函数\(y=-x^2+2x\)的图像仅有一个交点。参考图像

具体用手工怎么作图呢，函数\(y=-x^2+2x\)的图像大家应该会的，故重点说函数\(y=a(e^{x-1}+e^{-x+1})\)的图像做法。

令函数\(g(x)=y=e^x+\cfrac{1}{e^x}=e^x+e^{-x}\)，则是偶函数，\(g(0)=2\)，

当\(x\ge 0\)时，\(g'(x)=e^x-e^{-x}\)，\(g'(x)\)单调递增，

故\(g'(x)\ge g'(0)=0\)，则函数\(g(x)\)在\([0，+\infty)\)上单调递增，又由偶函数可知，在\((-\infty，0]\)上单调递减，

这样我们就做出了函数\(g(x)=e^x+\cfrac{1}{e^x}\)的图像，然后将其向右平移一个单位，得到\(y=e^{x-1}+e^{-x+1}\)的图像，

前边的系数\(a\)的作用有两个，其一控制张角大小，其二控制函数最低点的位置，

就像函数\(y=a|x|\)中的\(a\)的作用一样的，所以我们就能用手工做出函数\(y=a(e^{x-1}+e^{-x+1})\)的图像，

要使得函数\(y=a(e^{x-1}+e^{-x+1})\)与函数\(y=-x^2+2x\)的图像仅有一个交点，

就需要函数\(y=a(e^{x-1}+e^{-x+1})\)的最小值\(a(e^{1-1}+e^{-1+1})=2a\)和函数\(y=-x^2+2x\)的最大值\(-1^2+2\times1=1\)相等，

故\(2a=1\)，解得\(a=\cfrac{1}{2}\)。

【法3】：构造函数法+函数的性质法；

函数\(f(x)=x^2-2x+a(e^{x-1}+e^{-x+1})=(x-1)^2+a[e^{x-1}+e^{-(x-1)}]-1\)，

令\(t=x-1\)，则\(g(t)=f(x-1)=t^2+a(e^t+e^{-t})-1\)，

由于\(g(-t)=t^2+a(e^t+e^{-t})-1=g(t)\)，故\(g(t)\)为偶函数，

由于函数\(f(x)\)有唯一零点，则函数\(g(t)\)也有唯一零点，

又函数\(g(t)\)是偶函数，即函数\(g(t)\)与\(t\)轴仅有一个交点，则\(g(0)=0\)，

代入得到\(2a-1=0\)，即\(a=\cfrac{1}{2}\)；

【法4】：函数\(f(x)=0\Leftrightarrow\) \(a(e^{x-1}+e^{-(x-1)})=-x^2+2x\)

\(e^{x-1}+e^{-(x-1)}\ge 2\sqrt{e^{x-1}\cdot e^{-(x-1)}}=2\)，当且仅当\(x=1\)时取到等号；

\(-x^2+2x=-(x-1)^2+1\leq 1\)；

若\(a>0\)时，\(a(e^{x-1}+e^{-(x-1)})\ge 2a\)，

要使\(f(x)\)仅有一个零点，则必有\(2a=1\)，解得\(a=\cfrac{1}{2}\)；

若\(a<0\)，则函数\(f(x)\)的零点不唯一，

综上，\(a=\cfrac{1}{2}\)；选C.

【法5】由\(f(x)=x^2-2x+a(e^{x-1}+e^{-x+1})\)，

得到\(f(2-x)=(2-x)^2-2(2-x)+a(e^{2-x-1}+e^{-(2-x)+1})=x^2-2x+a(e^{x-1}+e^{-x+1})\)，

所以\(f(2-x)=f(x)\)，故\(x=1\)是函数\(f(x)\)图像的对称轴。

由题意可知，函数\(f(x)\)有唯一的零点，

故只能是\(x=1\)，

即\(f(1)=1^2-2\times1+a(e^{1-1}+e^{-1+1})=0\)，

解得\(a=\cfrac{1}{2}\)，故选C.

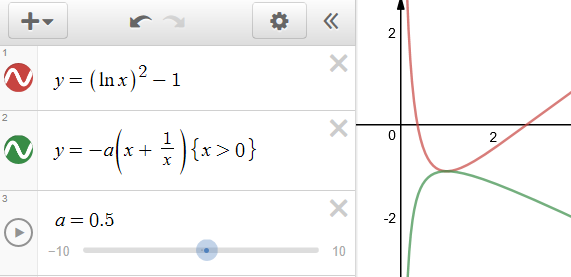
【法6】我们一般这样转化，由函数\(f(x)\)有唯一的零点，

得到方程\(x^2-2x=-a(e^{x-1}+e^{-x+1})\)有唯一解，注意到方程的右端，

我们可以和对勾函数做以联系，令\(x-1=t\)，则\(x=t+1\)，

故原方程就转化为\((t+1)^2-2(t+1)=-a(e^t+e^{-t})\)，为了便于做出图像，

还需要再代换，令\(e^t=x\)，则\(x>0\)且\(t=lnx\)，

这样方程就又转化为\(ln^2x-1=-a(x+\cfrac{1}{x})\)，

在同一个坐标系中，分别做出函数\(y=ln^2x-1\)和\(y=-a(x+\cfrac{1}{x})\)的图像，

由图像可知对勾函数前面的系数必须满足\(-a=-\cfrac{1}{2}\)，

即\(a=\cfrac{1}{2}\)，故选C.

【2017\(\cdot\)全国卷3理科第12题】函数\(f(x)=mx^2-2x+1\)有且只有一个正实根零点，则实数\(m\)的取值范围是【】

$A.(-\infty，0)$ $B.(-\infty，0]\cup\{1\}$ $C.(-\infty，0)\cup\{1\}$ $D.(-\infty，1]$

【法1】：验证法；

令\(m=0\)，则由\(-2x+1=0\)可得一个正实根\(x=\cfrac{1}{2}\)，故\(m=0\)满足题意，排除\(C\)；

令\(m=1\)，则由\((x-1)^2=0\)可得一个正实根\(x=1\)，故\(m=1\)满足题意，排除\(D\)；

令\(m=\cfrac{1}{2}\)，则由\(\cfrac{1}{2}x^2-2x+1=\cfrac{1}{2}(x-2)^2-1=0\)可得两个正实根\(x=2\pm\sqrt{2}\)，排除\(A\)；

故选\(B\).

【法2】：分类讨论法；

注意到函数\(f(x)=mx^2-2x+1\)为仿二次函数，故想到需要分类讨论，令\(f(x)=mx^2-2x+1=0\)，注意隐含条件\(f(0)=1\)

\(1^{\circ}\)当\(m=0\)时，由\(-2x+1=0\)可得一个正实根\(x=\cfrac{1}{2}\)，故\(m=0\)满足题意；

\(2^{\circ}\)当\(m>0\)时，抛物线开口向上，\(f(0)=1\)，对称轴为\(x=\cfrac{1}{m}>0\)，只能\(\Delta=4-4m=0\)，

可得一个正实根\(x=\cfrac{1}{m}\)，解得\(m=1\)；

\(3^{\circ}\)当\(m<0\)时，抛物线开口向下，\(f(0)=1\)，对称轴为\(x=\cfrac{1}{m}<0\)，

要满足题意只需\(\Delta=4-4m>0\)即可，解得\(m<0\)；

综上所述，\(m\)的取值范围为\((-\infty，0]\cup\{1\}\)，选B。

【法3】：分离参数法，由于函数有且只有一个正零点，

在\(x>0\)时，分离参数得到\(m=\cfrac{2x-1}{x^2}(x>0)\)，

要使得原函数有且只有一个正零点，只需要函数\(y=m\)和函数\(g(x)=\cfrac{2x-1}{x^2}(x>0)\)，

在\(x>0\)时的图像的交点有且仅有一个即可。

用导数研究函数\(g(x)=\cfrac{2x-1}{x^2}(x>0)\)的单调性，然后做出简图，此处简略。

在同一坐标系中，做出函数\(y=m\)和\(g(x)=\cfrac{2x-1}{x^2}(x>0)\)的图像，

由图像可得，\(m\)的取值范围为\((-\infty，0]\cup\{1\}\)。

补充：用导数研究函数\(g(x)=\cfrac{2x-1}{x^2}\)的单调性，

\(g'(x)=\cfrac{-2(x^2-1)}{x^4}\)，

令\(g'(x)>0\)的\(0<x<1\)；令\(g'(x)<0\)的\(x>1\)；

故函数\(g(x)\)在区间\((0，1]\)上单调递增，在区间\([1，+\infty)\)上单调递减，

又\(g(1)=1\)，然后就能手动做出函数图像。

【2017\(\cdot\)山东卷】已知当\(x\in[0，1]\)时，函数\(y=f(x)=(mx-1)^2\)的图像与\(y=g(x)=\sqrt{x}+m\)的图像有且只有一个交点，则正实数\(m\)的取值范围是【】

$A.(0，1]\cup[2\sqrt{3}，+\infty)$

$B.(0，1]\cup[3，+\infty)$

$C.(0，\sqrt{2}]\cup[2\sqrt{3}，+\infty)$

$D.(0，\sqrt{2}]\cup[3，+\infty)$

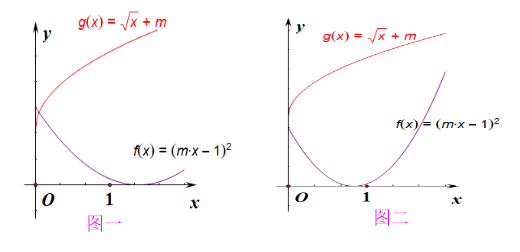
分析：这类题目总的解决途径无非是从形的角度和从数的角度两个方面思考：

法1：从形的角度，自然需要我们对常见函数的图像以及所含参数\(m\)的含义要非常清楚才行。

注意到两个函数图像都会随着参数\(m\)的取值变化而变化，都是动图。

第一种情形，如图一所示，二者在对称轴\(x=\cfrac{1}{m}\)的左侧只有一个交点，右侧不能有交点

则有\(\begin{cases}f(0)\ge g(0)\\ f(1)<g(1)\end{cases}\)，即\(\begin{cases}1\ge m\\ (m-1)^2<m+1\end{cases}\)，

\(0<m\leq 1\)；

第二种情形，如图二所示，二者在对称轴\(x=\cfrac{1}{m}\)的左侧没有交点，右侧只有一个交点

则有\(\begin{cases}f(0)< g(0)\\ f(1)\ge g(1) \end{cases}\)，即\(\begin{cases}1< m\\ (m-1)^2\ge m+1 \end{cases}\)，

\(m\ge 3\)；

综上所述，\(m\)的取值范围为\((0，1]\cup[3，+\infty)\) ，选\(B\).

【2019湖北七校联考】已知函数\(f(x)\)是奇函数且是\(R\)上的单调函数，若函数\(y=f(2x^2+1)+f(\lambda-x)\)只有一个零点，则实数\(\lambda\)的值为【】

$A.\cfrac{1}{4}$ $B.\cfrac{1}{8}$ $C.-\cfrac{7}{8}$ $D.-\cfrac{3}{8}$

分析：令\(y=f(2x^2+1)+f(\lambda-x)=0\)，则\(f(2x^2+1)=-f(\lambda-x)=f(x-\lambda)\)，

由于函数\(f(x)\)是\(R\)上的单调函数，故\(2x^2+1=x-\lambda\)，

即方程\(2x^2-x+1+\lambda=0\)只有一个实根，

则由\(\Delta=1-8(1+\lambda)=0\)，解得\(\lambda=-\cfrac{7}{8}\)，故选\(C\)。

求所有零点之和

已知函数\(f(x)=\left\{\begin{array}{l}{ln(-x)，x<0}\\{e^x+e^{2-x}-a，x\ge 0}\end{array}\right.\)，若\(f(x)\)的所有零点之和为\(1\)，则实数\(a\)的取值范围是\((2e，e^2+1)\)；

【分析】容易求出其中一个零点\(x=-1\)，然后研究\(x\ge 0\)时的函数\(f(x)\)的对称性，由图像的对称性和单调性得出函数在\(x\ge 0\)上的两个对称的零点的条件，从而得到\(a\)的取值范围。

【解答】当\(x<0\)时，由\(ln(-x)=0\)，得到函数的一个零点是\(x=-1\)，

当\(x\ge 0\)时，\(f(x)=e^x+e^{2-x}-a\)，\(f(2-x)=e^{2-x}+e^x-a\)，故\(f(x)=f(2-x)\)，即此时函数\(f(x)\)的图像关于直线\(x=1\)对称(此时函数图像部分对称，若去掉\(x\ge 0\)的限制，函数图像完全对称)，此时函数若有零点，则必然满足\(x_1+x_2=2\)，故所有零点之和为1，满足题意；

又\(f'(x)=e^x-e^{2-x}\)，当\(x\in (0，1)\)时，\(f'(x)<0\)，即\(f(x)\)单调递减，当\(x\in (1，+\infty)\)时，\(f'(x)>0\)，即\(f(x)\)单调递增，

故函数\(f(x)_{min}=f(1)=e^1+e^{2-1}-a=2e-a\)；

但要使得函数\(f(x)\)有零点必须满足条件\(f(x)_{min}<0\)且\(f(0)>0\)，（这是为了保证函数有两个零点，且在\((0，1)\)段上的零点必须存在）

即\(2e-a<0\)且\(e^0+e^2-a>0\)，解得\(2e<a<e^2+1\)，

【点评】①本题目考查函数的零点，考查的很灵活，借助图像类似开口向上的抛物线的函数的对称性考查零点的存在性，很有创意，而且我们一般很难想到研究函数的对称性。大多可能会朝对勾形函数做转化，结果思路变得模糊而不可解。
②对抽象函数而言，当我们看到条件\(f(x)=f(2-x)\)，肯定能想到函数有对称轴\(x=1\)，但碰到具体的函数我们却往往想不到用\(f(x)=f(2-x)\)来判断函数的对称性。

已知函数没有零点

【2020届高三文科训练题】若函数\(f(x)=\cfrac{ax-a}{e^x}+1(a<0)\)没有零点，则实数\(a\)的取值范围为________.

法1：利用导数方法求解，\(f'(x)=\cfrac{-a(x-2)}{e^x}(a<0)\)，

当\(x<2\)时，\(f'(x)<0\)，函数\(f(x)\)单调递减，

当\(x>2\)时，\(f'(x)>0\)，函数\(f(x)\)单调递增，

故当\(x=2\)时，\(f(x)_{min}=f(2)=\cfrac{a}{e^2}+1\)，

若要使的函数没有零点，当且仅当\(f(2)=\cfrac{a}{e^2}+1>0\)，

解得\(a>-e^2\)，又\(a<0\)，故\(a\in (-e^2，0)\)；

法2：函数\(y=a(x-1)(a<0)\)与函数\(y=-e^x\)没有交点，数形结合求解得到，\(a\in (-e^2，0)\).

相关零点最值

【2018广东中山期末】已知\(\cfrac{1}{3}\leq k<1\)，函数\(f(x)=|2^x-1|-k\)的零点分别为\(x_1\)、\(x_2\)，\((x_1<x_2)\)，函数\(g(x)=|2^x-1|-\cfrac{k}{2k+1}\)的零点分别为\(x_3\)、\(x_4\)，\((x_3<x_4)\)，则\(x_4+x_2-(x_3+x_1)\)的最小值为【】

$A.1$ $B.log_23$ $C.log_26$ $D.4$

分析：函数\(f(x)\)的零点问题，转化为函数\(y=|2^x-1|\)与\(y=k\)的图像交点的横坐标问题，同理，函数\(g(x)\)的零点问题，转化为函数\(y=|2^x-1|\)与\(y=\cfrac{k}{2k+1}\)的图像交点的横坐标问题，

又由于\(y=\cfrac{k}{2k+1}=\cfrac{1}{2+\frac{1}{k}}\)，在\(k\in [\cfrac{1}{3}，1)\)上单调递增，即当\(k\)的取值从\(\cfrac{1}{3}\)增大到\(1\)时，\(\cfrac{k}{2k+1}\)的取值对应的从\(\cfrac{1}{5}\)增大到\(\cfrac{1}{3}\)，

做出如下的图像，从图像入手分析，当\(y=k\)向上平移时，\(x_2-x_1\)逐渐增大，同理对应的\(x_4-x_3\)逐渐增大，所以要使得\(x_4+x_2-(x_3+x_1)\)取到最小值，则需要\(x_4-x_3\)和\(x_2-x_1\)同时取到最小值，此时\(k=\cfrac{1}{3}\)，同时对应的有\(\cfrac{k}{2k+1}=\cfrac{1}{5}\)；

此时，\(|2^{x_2}-1|=\cfrac{1}{3}\)，即\(2^{x_2}-1=\cfrac{1}{3}\)，解得\(x_2=log_2\cfrac{4}{3}\)，又\(|2^{x_1}-1|=\cfrac{1}{3}\)，即\(1-2^{x_1}=\cfrac{1}{3}\)，解得\(x_1=log_2\cfrac{2}{3}\)，

同理对应的有\(|2^{x_4}-1|=\cfrac{1}{5}\)，即\(2^{x_4}-1=\cfrac{1}{5}\)，解得\(x_4=log_2\cfrac{6}{5}\)，又\(|2^{x_3}-1|=\cfrac{1}{5}\)，即\(1-2^{x_3}=\cfrac{1}{5}\)，解得\(x_3=log_2\cfrac{4}{5}\)，

故此时\([x_4+x_2-(x_3+x_1)]_{min}=(log_2\cfrac{6}{5}-log_2\cfrac{4}{5})+(log_2\cfrac{4}{3}-log_2\cfrac{2}{3})=log_23\)，故选\(B\)。

解后反思：比如将条件更改为\(\cfrac{1}{3}\leq k\leq \cfrac{4}{5}\)，那么用相应的思路和方法，可以求解\(x_4+x_2-(x_3+x_1)\)的取值范围；

已知函数存在零点

【2019高三理科数学信息题】已知函数\(f(x)=x^2lnx+1-kx\)存在零点，则\(k\)的取值范围为【】

$A(-\infty，1]$ $B[1，+\infty)$ $C(-\infty，e]$ $D[e，+\infty)$

分析：已知函数\(f(x)=x^2lnx+1-kx\)存在零点，即方程\(f(x)=0\)在定义域\((0，+\infty)\)上有解，

分离参数得到\(k=\cfrac{x^2lnx+1}{x}=xlnx+\cfrac{1}{x}\)，令\(h(x)=xlnx+\cfrac{1}{x}\)，

则题目转化为\(k=h(x)\)在\((0，+\infty)\)上有解，故要么从数的角度求函数\(h(x)\)的值域；要么求其单调性，做函数的图像，从形的角度用数形结合求解。

以下用导数求函数\(h(x)\)的单调性。\(h'(x)=lnx+1-\cfrac{1}{x^2}\)，

此时需要注意，导函数中出现了\(lnx\)，故我们将上述的函数人为的分为两个部分，\(y=lnx\)和\(y=1-\cfrac{1}{x^2}\)，先令\(lnx=0\)得到\(x=1\)，在将\(x=1\)代入\(y=1-\cfrac{1}{x^2}\)验证也是其零点，说明这两个函数的零点重合，故接下来我们将定义域分为\((0，1)\)和\((1，+\infty)\)两部分分类讨论即可：

则\(0<x<1\)时，\(h'(x)<0\)，\(h(x)\)单调递减，\(x>1\)时，\(h'(x)>0\)，\(f(x)\)单调递增，则\(h(x)_{min}=h(1)=1\)。

即\(h(x)\)的值域为\([1，+\infty)\)，故\(k\ge 1\)，即\(k\in [1，+\infty)\)。故选\(B\)

或利用单调性得到函数\(h(x)\)的图像如下，

再利用函数\(y=k\)和函数\(y=h(x)\)的图像有交点，得到\(k\)的取值范围为\(k\in [1，+\infty)\)。故选\(B\)

函数 \(f(x)=x\cdot\cos x^{2}\) 在 \([-4,4]\) 上的零点个数为_____________.

解析： 令 \(f(x)=0\)， 得 \(x=0\) 或 \(\cos x^{2}=0\)，

由 \(\cos x^{2}=0\) 知 \(x^{2}=\cfrac{\pi}{2}+k\pi\)， \(k\in Z\)， 又 \(x\in[-4,4]\)， 则\(x^{2} \in[0,16]\)，

\(x^{2}=\cfrac{\pi}{2}\) 或 \(\cfrac{3 \pi}{2}\) 或 \(\cfrac{5 \pi}{2}\) 或 \(\cfrac{7 \pi}{2}\) 或 \(\cfrac{9 \pi}{2}\)，此时 \(x\) 有 10 个解，

综上 \(f(x)\) 在 \([-4,4]\) 上有 11 个零点。

可化情形

函数\(f(x)\)有极值，则导函数\(y=f'(x)\)应该有变号零点。