前言
为什么要用图像解不等式?自然是用数的角度不能顺利求解,要么不等式是超越不等式,要么是抽象不等式,或者是分段函数不等式等等;总之一句话,从数的角度思考不能解决的,都可以尝试考虑换个角度,从形入手分析。
求解原理
定义域值域
题型解法
用图像解抽象或分段不等式
函数 f(x) 是周期为 4 的偶函数,当 x∈[0,2] 时,f(x)=x−1,求不等式 x⋅f(x)>0 在 [−1,3] 上的解集。
解法思路:利用条件先做出抽象函数的图像,然后读图解不等式
法 1:自己作图如右,读图即可解答,解集为 (−1,0)∪(1,3);
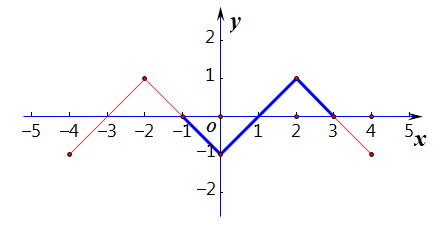
法 2:利用积的符号法则求解,
原不等式等价于 {x>0f(x)>0 或 {x<0f(x)<0,
读图即可解答,解集为 (−1,0)∪(1,3);
感悟反思:1、学图像,用图像,天经地义。2、熟练掌握分段函数的图像,对解题很有帮助。
【2020 届高三文科数学用题】设函数 y=f(x+1) 是定义在 (−∞,0)∪(0,+∞) 上的偶函数,在区间 (−∞,0) 上是减函数,且图像经过点 (1,0),则不等式 (x−1)⋅f(x)⩽0 的解集为______。
分析:由于 f(x+1) 为偶函数,故其满足 f(−x+1)=f(x+1),则函数 f(x) 的对称轴为 x=1,
可以先做出函数 y=f(x+1) 的示意图,再向右平移一个单位得到函数 y=f(x) 的示意图如下,
不等式 (x−1)⋅f(x)⩽0 可化为 {x>1f(x)⩽0 或 {x<1f(x)⩾0
解读图像可知,解集为 {x∣x⩽0或1<x⩽2},故 x∈(−∞,0]∪(1,2].
用图像解超越不等式
解关于 x 的不等式 lnx>1−x;
解法思路:利用条件先做出抽象函数的图像,然后读图解不等式
分析:你应该能感觉到,这个题目用我们平常的那种解法 (代数解法) 已经不能做出来了,
因为它不是我们熟悉的那种代数不等式,而是超越不等式,这时候就需要我们借助图像来求解。
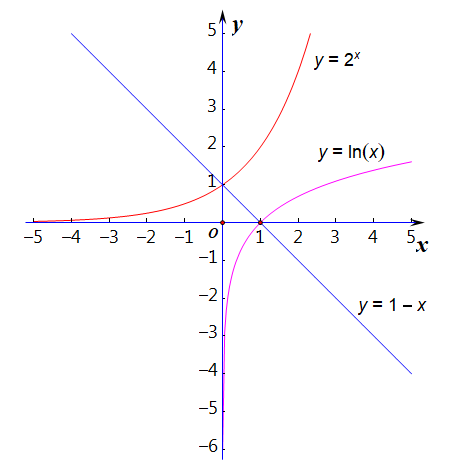
比如分别作出两个函数 y=lnx 和 y=1−x 的图像观察求解,如右图所示,解集为 (1,+∞);
思路 2:从数的角度,利用函数计算,令 g(x)=lnx+x−1(x>0),
则 g′(x)=1x+1>0 恒成立,故 g(x) 在 (0,+∞) 上单调递增,
又 g(1)=0,故 0<x<1 时,g(x)<0,x>1 时 g(x)>0,
综上,故 x 的取值范围为 (1,+∞)。
感悟反思:1、同类题目牛刀小试一下;2、超越不等式
用图像解构造的函数不等式
【2015⋅ 全国卷 2】设函数 f′(x) 是奇函数 f(x)(x∈R) 的导函数,f(−1)=0,当 x>0 时,xf′(x)−f(x)<0,则使得 f(x)>0 成立的 x 的取值范围是【】
A.(−∞,−1)∪(0,1) B.(−1,0)∪(1,+∞) C.(−∞,−1)∪(−1,0) D.(0,1)∪(1,+∞)
解法思路:利用条件先做出导函数的图像,然后读图解不等式
【法 1】注意到 xf′(x)−f(x)<0,故构造函数 g(x)=f(x)x,则函数 g(x) 为偶函数;
g′(x)=xf′(x)−f(x)x2,结合当 x>0 时,xf′(x)−f(x)<0,
可知,当 x>0 时,g′(x)<0,即 g(x) 在 (0,+∞) 上单调递减,
由偶函数可知,g(x) 在 (−∞,0) 上单调递增,
又 f(−1)=0,即 g(−1)=f(−1)−1=0,且 g(1)=g(−1)=0,
从而做出 g(x) 的图像如图所示,
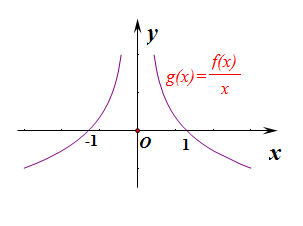
以下说明如何利用 g(x) 的图像解不等式 f(x)>0;
第一象限的函数图像 (注意此时有 0<x<1),满足 g(x)=f(x)x>0 且 x>0,
由符号法则得 f(x)>0,将这段函数图像向 x 轴作射影,
得到 0<x<1,即当 0<x<1 时,必有 f(x)>0 成立;
同理可知,由第二象限的图像,注意此时有 −1<x<0 及 g(x)>0,可得当 −1<x<0 时,必有 f(x)<0,不符;
同理,由第三象限的图像,注意此时有 x<−1 及 g(x)>0,可得当 x<−1 时,必有 f(x)>0,符合;
同理,由第四象限的图像,注意此时有 x>1 及 g(x)<0,可得当 x>1 时,必有 f(x)<0,不符;
综上所述,f(x)>0 的解集是 (−∞,−1)∪(0,1)。选 A
【法 2】有了法 1 做基础,我们可以简化如下,y 轴右侧的图像,代表 x>0,
那么 g(x)=f(x)x 的分母就为正,现在要求解 f(x)>0,此时必然会选择 x 轴上方的图像,其满足 g(x)>0,
故将这段图像向 x 轴作射影,落在区间 (0,1) 上,故有 0<x<1 时,f(x)>0;
而 y 轴左侧的图像,代表 x<0,
那么 g(x)=f(x)x 的分母就为负,现在要求解 f(x)>0,此时必然会选择 x 轴下方的图像,其满足 g(x)<0,
故将这段图像向 x 轴作射影,落在区间 (−∞,−1) 上,说明 x<−1 时,f(x)>0;
综上所述,f(x)>0 的解集是 (−∞,−1)∪(0,1)。选 A
感悟反思:若 g(x)=x⋅f(x) 或者 g(x)=f(x)x,由符号法则可知,g(x) 的正负取决于其因子 x 和 f(x) 的正负;
【构造函数】【构造函数解不等式】设 f(x),g(x) 分别是定义在 R 上的奇函数和偶函数,且 g(x)≠0,当 x<0 时 f'(x)g(x)>f(x)g'(x),且 f(−3)=0,则不等式 f(x)g(x)<0 的解集是______.
分析:令 h(x)=f(x)g(x),则可知 h(x) 为奇函数,
则 h′(x)=f′(x)g(x)−f(x)g′(x)g2(x),
由 x<0 时 f'(x)g(x)>f(x)g'(x),
可得 x∈(0,+∞) 时,h′(x)>0,即 h(x) 单调递增,
由奇函数可知,x∈(−∞,0) 时,h(x) 单调递增,
且 h(0)=0,由 f(−3)=0 还可得到 h(−3)=h(3)=0
做出示意图,由图可知,
故由 h(x)=f(x)g(x)<0,可得 x∈(−∞,−3)∪(0,3)。
又 f(x)g(x)<0 等价于 f(x)g(x)<0,
故不等式 f(x)g(x)<0 的解集是 x∈(−∞,−3)∪(0,3)。
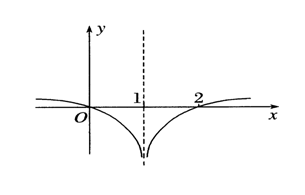
已知函数 f(x)=lgx+(a−2)x−2a+4(a>0), 若有且仅有两个整数 x1,x2 使得 f(x1)>0, f(x2)>0, 则 a 的取值范围是【】
A.(0,2−lg3] B.(2−lg3,2−lg2] C.(2−lg2,2] D.(2−lg3,2]
解: 由 f(x)=lgx+(a−2)x−2a+4>0, 得 lgx>(2−a)x+2a−4
由题意可知,满足不等式 lgx>(2−a)x+2a−4 的解中有且只有两个整数,
即函数 y=lgx 在直线 y=(2−a)x+2a−4 上方的图象中有且只有两个横坐标为整数的点,如图所示,
由图像可知,由于 y=(2−a)x+2a−4=(2−a)(x−2),该直线过定点 (2,0),如果想要了解更多,请参阅博文函数或曲线恒过定点
要使得函数 y=lgx 在直线 y=(2−a)x+2a−4 上方的图象中有且只有两个横坐标为整数的点,
则有 {2−a>0lg3⩽3(2−a)+2a−4 说明此处如果令 2−a⩽0,则不等式的解集中会有无穷多的整数,则不满足题意;不太好理解的是不等式 lg3⩽3(2−a)+2a−4 为什么要取到等号。当取得等号时,由于不等式是 lgx>(2−a)x+2a−4,故解集中不会有 x=3,故此处必须取到等号;
即 {a<22−a⩾lg3 解得,a⩽2−lg3,
又由于 a>0,故 0<a⩽2−lg3,故选 A.
【2021 - 山东德州二模】 已知定义在 (−∞,0)∪(0,+∞) 上的奇函数 f(x) 在 (−∞,0) 上单调递增, 且满足 f(−1)=−2, 则关于 x 的不等式 f(x)<2x+sinπx 的解集为 【】
A.(−∞,−1)∪(1,+∞) B.(−1,0)∪(1,+∞) C.(−∞,−1)∪(0,1) D.(−1,0)∪(0,1)
〔分析〕:本题目涉及到函数的拆分构造,函数性质的判断,利用函数图像解不等式等比较高深的数学知识,对学生的能力有一定的要求,也能较好的区分学生的数学素养。
其一:由于要解的不等式为 f(x)<2x+sinπx ,观察其结构,发现其构成部分中,y=f(x) 为抽象函数且为奇函数,y=sinπx 是超越函数,故整个不等式应该是超越不等式,其求解不能采用代数方法,而应该利用函数的图像来解不等式;
其二:当我们考虑要做不等式两端的函数图像时发现,y=f(x) 的图像好做,但是 y=2x+sinπx 的图像不好做,注意到 y=2x 为奇函数,而 y=f(x) 也是奇函数,故可以将二者通过移向加以整合为一个奇函数,从而其图像变得可做,剩余的 y=sinπx 的图像我们是会做的,这样从形的角度求解不等式的思路就打通了;
其三:在具体作图中,会涉及到两个函数的图像的位置关系问题,到时间可以利用特殊点的位置高低来确定。
〔解析〕: 由于 f(x) 为 (−∞,0)∪(0,+∞) 上的奇函数,故满足 f(−x)=−f(x),
令 g(x)=f(x)−2x 其实此处用 “奇 + 奇 = 奇”,就可以快速判断整合后的函数的奇偶性。, 则 g(−x)=f(−x)+2x=−f(x)+2x=−g(x),
所以 g(x) 为 (−∞,0)∪(0,+∞) 上的奇函数;
由于 f(x) 在 (−∞,0) 上单调递增, y=−2x 在 (−∞,0) 上单调递增,
则 g(x) 在 (−∞,0) 上单调递增其实此处用 “增 + 增 = 增”,就可以快速判断整合后的函数的单调性。, 由奇函数性质知 g(x) 在 (0,+∞) 上单调递增;
又由于 f(−1)=−2, 则 g(−1)=f(−1)+2=0, 则由 g(x) 为奇函数可知 g(1)=−g(−1)=0,
又 f(52)>f(1)=−f(−1)=2, 则 g(52)=f(52)−252=f(52)−45>1,
而 当 x=52 时, sinπx=sin5π2=1, 故有 g(52)>sin5π2 ,
由此可在坐标系中画出 g(x) 与 y=sinπx 大致图象如下图其中 y=sinπx 的图像大家应该能做,而做函数 y=g(x) 图像时要注意,y 轴是其渐近线,在 (0,+∞) 上单调递增,且经过点 (1,0) ,通过上述的计算可知,在 (1,+∞) 上 y=g(x) 与 y=sinπx 两个函数图像再没有交点。所示:
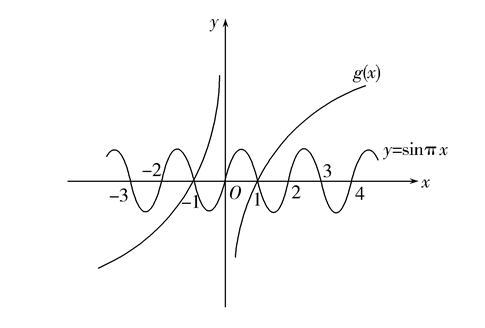
这样,原本的不等式,g(x)<sinπx 就从形的角度刻画出来了,大小关系体现在图像是变成了图像位置的高低关系了,通过读图可知:
当 x∈(−∞,−1)∪(0,1) 时, g(x)<sinπx, 即当 x∈(−∞,−1)∪(0, 1) 时, f(x)<2x+sinπx 。
记事备忘
有时间补充,用图像解三角不等式、对数不等式、指数不等式等等,还有代数不等式,如二次不等式;一次不等式,分式不等式,高次不等式等等。
延伸阅读
用导函数的图像判断原函数的单调性;


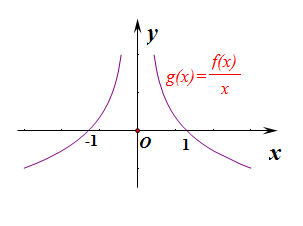

 当题目给定一个不等式让我们求解时,我们一般的思维都是想着从数的角度求解,但是不是所有的不等式都能从数的角度利用代数方法求解,比如给定的不等式为抽象不等式,或者超越不等式等,此时从数的角度就没法展开,必须从形的角度入手分析,将不等式两端的大小关系体现在图像上,变成图像位置的高低关系,通过读图就可解。
当题目给定一个不等式让我们求解时,我们一般的思维都是想着从数的角度求解,但是不是所有的不等式都能从数的角度利用代数方法求解,比如给定的不等式为抽象不等式,或者超越不等式等,此时从数的角度就没法展开,必须从形的角度入手分析,将不等式两端的大小关系体现在图像上,变成图像位置的高低关系,通过读图就可解。





【推荐】国内首个 AI IDE,深度理解中文开发场景,立即下载体验 Trae
【推荐】编程新体验,更懂你的 AI,立即体验豆包 MarsCode 编程助手
【推荐】抖音旗下 AI 助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· winform 绘制太阳,地球,月球 运作规律
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具
· AI 智能体引爆开源社区「GitHub 热点速览」