分离参数法
💎更新于 2024-12-11 14:46 | 发布于 2018-06-28 17:50
约 14975 字 | 阅读估时 50 分钟
前言
在高中数学教学实践中,有一种使用频度比较高的数学方法,叫分离参数法,她和许多数学素材有关联,高三学生大多都耳熟能详,但对其具体的来由和需要注意的问题却不是很清楚,本博文试着对此做个总结,以廓清我们认识上的误区,帮助我们提高教学,也帮助学生顺利掌握这一方法。
使用场景
【法 1】:不完全分离参数法,先确定函数的定义域为 (0,+∞),将函数 f(x) 有两个零点转化为方程 kx2=lnx 有两个不同的实数根,再转化为函数 y=kx2 与函数 y=lnx 的图像有两个不同的交点,如图设两个函数的图像相切于点为 (x0,y0),则必有以下关系式成立 [列等式的角度是难点] 从三个角度列方程:两曲线在切点 (x0,y0) 处的斜率相等;切点 (x0,y0) 在曲线一上;切点 (x0,y0) 在曲线二上;
由 ① 得到 2kx20=1,代入 ② 式,解得 y0=12,x0=√e,即切点为 (√e,12),
再代入函数 y=kx2,求得此时的 k=12e,
再结合函数 y=kx2 的系数 k 的作用,可得两个函数要有两个不同的交点,
则 k∈(0,12e)。 故选 D.
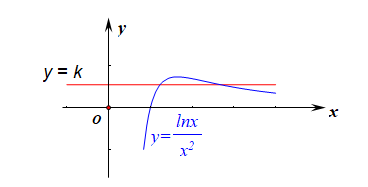
【法 2】:完全分离参数法,首先确定函数的定义域为 (0,+∞),将函数有两个零点转化为方程 kx2=lnx 有两个不同的实数根, 再完全分离参数转化为 k=lnxx2 有两个不同的实数根, 再转化为函数 y=k 和函数 y=g(x) = lnxx2 的图像有两个不同的交点, 用导数研究函数 g(x) 的单调性,
由于 g′(x)=1x⋅x2−lnx⋅2x(x2)2=1−2lnxx3,
令 1−2lnx>0,得到 0<x<√e ;令 1−2lnx<0,得到 x>√e,
即函数 g(x) 在区间 (0,√e] 上单调递增,在 [√e,+∞) 上单调递减,
故 g(x)max=g(√e)=12e,
作出函数 g(x) 的图象和函数 y=k 的简图,由图像可得 k 的取值范围是 k∈(0,12e),故选 D.
- 从上述的解法中我们体会到,如果一个数学题目从数的角度直接来求解,结果很有可能要么不会求解,要么解不出,更或者没有思路;此时若换个角度思考,从形入手分析,将参数或含有参数的代数式 (比如 k+1) 和自变量分别放置在等号的两端,即 k=f(x) 的形式,然后数的问题就转化为形的问题了,从而直观快捷,思路简单明了。 一句话,当我们从形的角度入手分析解题时,接下来使用的方法常常是分离参数法。
常见类型
- ①完全分离参数法:如 λf(x)=g(x)⇒λ=g(x)f(x);
引例,已知函数 f(x)=kx2−lnx 有两个零点,求参数 k 的取值范围,用常规法分离参数,即得到方程 k=lnxx2 有两个不同实根,具体解法链接。
分析:由题目可知,f′(x)≥0 在 (1,+∞) 上恒成立,且 f′(x) 不恒为零,
则有 f′(x)=mx+2x−m=2x2−mx+mx≥0 在 (1,+∞) 上恒成立,
即 2x2−mx+m≥0 在 (1,+∞) 上恒成立,常规法分离参数得到
m≤2x2x−1=2(x−1)2+4x−2x−1=2(x−1)2+4(x−1)+2x−1=2(x−1)+2x−1+4
由于 x>1,故 2(x−1)+2x−1+4≥2√4+4=8,当且仅当 x=2 时取到等号。
故 m≤8,当 m=8 时,函数不是常函数,也满足题意,故 m∈(−∞,8]。
- ②倒数法分离参数:如 λf(x)=g(x)⇒1λ=f(x)g(x);
引例,方程 kx2=ex,若常规法分离参数得到 k=exx2,就没有倒数法分离为 1k=x2ex 优越,
原因是函数 y=exx2 在 x=0 处有断点,而函数 y=x2ex 在 x∈R 上是处处连续的,函数相对简单一些。
分析:不妨设 m>n,则函数 f1(x) 在区间 [0,1] 上单调递增,故 f1(m)−f1(n)>0,
又 f2(x)=a(x−1)2+b−a,对称轴是 x=1,开口向上,
故函数 f2(x) 在区间 [0,1] 上单调递减,故 f2(m)−f2(n)<0,
这样对任意的 m,n∈[0,1](m>n),|f1(m)−f1(n)|>|f2(m)−f2(n)| 恒成立,
就可以转化为 f1(m)−f1(n)>f2(n)−f2(m) 恒成立,
即 f1(m)+f2(m)>f1(n)+f2(n) 恒成立,
令 h(x)=f1(x)+f2(x)=ex+ax2−2ax+b,
则到此的题意相当于已知 m>n 时,h(m)>h(n),
故函数 h(x) 在区间 [0,1] 上单调递增,故 h′(x)≥0 在区间 [0,1] 上恒成立;
即 h′(x)=ex+2ax−2a≥0 在区间 [0,1] 上恒成立;
即 2a(1−x)≤ex 恒成立,这里我们使用倒数法分离参数得到,
12a≥1−xex 在区间 [0,1] 上恒成立;
再令 p(x)=1−xex,即需要求 p(x)max,
p′(x)=−1×ex−(1−x)ex(ex)2=x−2ex,
容易看出,当 x∈[0,1] 时,p′(x)<0 恒成立,故 p(x) 在区间 [0,1] 上单调递减,
则 p(x)max=p(0)=1,故 12a≥1,又 a>0,
故解得 0<a≤1。故 amax=1.
- ③讨论法分离参数:如 λf(x)≥g(x);
比如,λ(x−1)≥2lnx 对任意的 x∈(0,1] 恒成立,接下来分 x=1 和 0<x<1 分类讨论分离参数,具体见博文的后半部分的对应例题。
分析:对任意 x>0 且 x≠1,不等式 x−mlnx>√x 恒成立等价于
当 0<x<1 时,m>x−√xlnx① 恒成立,或者当 x>1 时,m<x−√xlnx② 恒成立,
令 h(x)=x−√xlnx(x>0,x≠1),h′(x)=2√x−lnx−22√x
令 ϕ(x)=2√x−lnx−2,则 ϕ′(x)=√x−1x;
易知 ϕ(x) 在 (0,1) 上单调递减,在 (1,∞) 上单调递增,
所以 ϕ(x)>ϕ(1)=0,即得到 h′(x)>0,
因此由①式可得,m≥h(1)=1,由②式得 m≤h(1)=1
取两种结果的交集 [1],所以 m=1。
故不等式 x−mlnx>√x 恒成立的充要条件是 m=1。
- ④整体法分离参数:如 λ2+2λ=f(x);
分析:由题目可知,命题 “¬P:∀x∈R,2x−2>a2−3a” 是真命题,
即 2x−2>a2−3a 对 ∀x∈R 恒成立,故 (2x−2)min>a2−3a,
只需求 (2x−2)min,而 2x−2>−2,则有 −2≥a2−3a,即 a2−3a+2≤0,
解得 1≤a≤2,故实数 a 的取值范围是 [1,2]。
分析:先由 f(1−x)=f(1+x) 得到,二次函数的对称轴 x=−a−2=1,解得 a=2,
故题目转化为 −x2+2x+b2−b+1>0 对任意 x∈[−1,1] 恒成立,
用整体法分离参数,得到 b2−b>x2−2x−1 对任意 x∈[−1,1] 恒成立。
令 g(x)=x2−2x−1,x∈[−1,1],需要求函数 g(x)max;
g(x)=x2−2x−1=(x−1)2−2,x∈[−1,1],
故 g(x) 在区间 [−1,1] 上单调递减,则 g(x)max=g(−1)=2,
故 b2−b>2,解得 b<−1 或 b>2。
法 2:还可以利用对称轴与给定区间的关系求解;
- ⑤不完全分离参数法:如 kx2=lnx;
比如,已知函数 f(x)=kx2−lnx 有两个零点,求参数 k 的取值范围,用不完全分离参数法,即得到方程 kx2=lnx 有两个不同实根,具体解法链接。
局限之处
并不是所有的含参问题都适合分离参数,比如 ax2−a2x+3<0 在区间 [1,2] 上恒成立,求 a 的范围,就不能用分离参数的方法,因为你没法将参数和自变量有效的分开,所以此时你可能需要借助二次函数的图像来考虑,而不是一味的使用分离参数法。
一般来说,以下的一些情形都不适合使用分离参数法:
- (1) 不能将参数和自变量有效的分离开的;
比如,已知方程 e−x=ln(x+a) 在 x>0 时有解,求参数的取值范围;
本题目就不能将参数和自变量有效的分离开的,此时我们就可以考虑用数形结合的思路求解。解法
- (2) 如果参数的系数能取到正、负、零三种情形的,
引例,已知函数 f(x)=x2+ax−2a≥0 对 x∈[1,5] 上恒成立,求参数 a 的取值范围。
如果用分离参数的方法,则先转化为 (x−2)a≥−x2,x∈[1,5]
接下来就转化成了三个恒成立的命题了,不管会不会做,从效率上都已经很不划算了。具体的解法已经隐藏。
- (3) 分离参数后,得到的新函数变得复杂无比的;
比如函数 f(x)=x2−2x+a(ex−1+e−x+1) 有唯一的零点,分离参数后,得到 a=−x2+2xex−1+e−x+1=h(x),
你确信你能研究清楚函数 h(x) 的性质,并用手工做出函数的图像吗?省省吧,您呐。
- (4) 分离参数后,得到的新函数中有 sinx 和 cosx 的,他们都有无穷阶导数,所以求导会一直做下去,一般不会使得函数式变得简单。
比如已知 2a−1+sin2x+a(sinx−cosx)≥0 在 x∈[0,π2] 上恒成立,求参数 a 的取值范围。[1,+∞)
接下来的思路有:
思路一:分离参数,当分离为 a≥1−sin2x2+sinx−cosx=g(x) 时,你会发现,求函数 g(x)max 很难,所以放弃;
思路二:转化化归,令 sinx−cosx=t=√2sin(x−π4),由于 x∈[0,π2],故 t∈[−1,1]
由 (sinx−cosx)2=t2,得到 sin2x=1−t2,故不等式转化为 at+1−t2+2a−1≥0,
即 t2−at−2a≤0 在 t∈[−1,1] 上恒成立,令 h(t)=t2−at−2a,t∈[−1,1],
则 h(t)≤0 等价于 {h(−1)=1+a−2a≤0h(1)=1−a−2a≤0,解得 a≥1,
或在转化化归后又可以分离参数为 a⩾t2t+2=g(t),t∈[−1,1] 恒成立问题,求 g(t) 的最大值即可 .
- (5) 看题目的选项确定方法
法 1:先考虑分离参数法,若能成功分离参数,那么得到的形式必然是 m>g(x) 或 m<g(x) 的形式,接下来需要求解函数 g(x) 的最值,其必然是数字化的,则结果和给定的选项的形式是不一致的,故这个思路做了大致分析后放弃;
法 2:由函数 f(x)>0 恒成立,则需要求在 (0,+∞) 上的函数 f(x)min>0 即可,故考虑用导数方法;
f′(x)=(x+1)[mx+(1−m)]x2, 故函数在 x=m−1m 处取到最小值,则要使得函数 f(x)>0 恒成立,只需要 f(m−1m)>0 即可,
对此化简整理得到,正实数 m 应该满足 m−1m⋅e2m−1>1,故选 C。
解后反思:本题目的解法有点漏洞,条件中应该使得 m>1,而不仅仅是 m>0,否则当 0<m≤1 时,函数 f(x) 在 (0,+∞) 上单调递增,其最小值的极限为 f(0),题目就有了问题。
策略延伸
在具体的解题实践中,我们会发现绝大多数的题目可以用分离参数法解决,但是如果简单尝试后发现此法行不通,则需要及时调整解题思路和策略,比如做差构造新函数的思路。
已知函数 f(x)=x2−ax,g(x)=mx+nlnx,函数 f(x) 的图像在点 (1,f(1)) 处的切线的斜率为 1,函数 g(x) 在 x=2 处取到极小值 2−2ln2;
(1) 求函数 f(x) 与 g(x) 的解析式;
分析:由题可知 f′(x)=2x−a,又 f′(1)=2−a=1,解得 a=1,即 f(x)=x2−x;
又 g′(x)=m+nx,由 g′(2)=m+n2=0 及 g(2)=2m+nln2=2−2ln2,解得 m=1,n=−2,即 g(x)=x−2lnx;
(2) 已知函数 f(x)+g(x)≥x2−λ(x−1) 对任意的 x∈(0,1] 恒成立,求实数 λ 的取值范围。
分析:由于 f(x)+g(x)=x2−2lnx,则 x2−2lnx≥x2−λ(x−1) 对任意的 x∈(0,1] 恒成立,可以有以下的思路:
法 1:带参分析法,先令 h(x)=λ(x−1)−2lnx,则问题转化为 h(x)≥0 对任意的 x∈(0,1] 恒成立,
h′(x)=λ−2x=λx−2x
当 λ≤0 时,h′(x)<0,h(x) 在区间 (0,1] 上单调递减,
h(x)min=h(1)=0,即 h(x)≥0 恒成立;
当 0<λ≤2 时,h′(x)<0,h(x) 在区间 (0,1] 上单调递减,
h(x)min=h(1)=0,即 h(x)≥0 恒成立;
当 λ>2 时,h′(x)<0 在 (0,2λ) 上恒成立,h′(x)>0 在 (2λ,1) 上恒成立,
即 h(x) 在 (0,2λ) 单调递减,在 (2λ,1) 上单调递增,
所以 h(2λ)<h(1)=0,故不满足题意,注意 h(1)=0,即函数 h(x) 恒过点 (1,0)
综上所述,实数 λ 的取值范围为 (−∞,2]。
法 2:讨论法分离参数,先转化为 λ(x−1)≥2lnx 对任意的 x∈(0,1] 恒成立,
当 x=1 时,λ⋅0≥2ln1=0,λ∈R;
当 x∈(0,1) 时,分离参数得到 λ≤2lnxx−1;令 h(x)=2lnxx−1,
h′(x)=2x(x−1)−2lnx(x−1)2=2(1−1x−lnx)(x−1)2;
令 m(x)=1−1x−lnx,则 m′(x)=1x2−1x=1−xx2,
则 m′(x)>0,则 m(x) 在 (0,1) 上单调递增,故 m(x)<m(1)=0,故 h′(x)=2m(x)(x−1)2<0,
则 h(x) 在 (0,1) 上单调递减,故 h(x)>h(1)=2(由洛必达法则求得),即 λ≤2
综上所述求交集得到,λ∈(−∞,2]。
法 3:不完全分离参数法,由 λ(x−1)≥2lnx 对任意的 x∈(0,1] 恒成立,
做函数 y=λ(x−1) 和函数 y=2lnx 的图像,示意图
设直线 y=λ(x−1) 与曲线 y=2lnx 相切于点 (x0,y0),则有 2x0=λ,y0=2lnx0,y0=λ(x0−1),
求得切点坐标 (1,0),此时 λ=2,由 λ 的几何意义可知,λ 的取值范围是 (−∞,2]。
注意事项
- 分离参数法,一般常用于恒成立问题、能成立问题 (有解),或无解问题,或已知函数零点个数命题中的参数取值范围问题,又或是从数的角度不好解决需要从形的角度入手的问题。
- 分离参数时,尽可能的使函数形式简单,这样求导数判断单调性就简单些,而参数形式复杂些或者简单些都无所谓,
(1) 若函数 f(x) 在区间 (0,12) 上无零点,求实数 a 的最小值。
【法 1】(分离参数,参数形式简单,函数复杂)
碰到这类问题,我们的第一反应往往是分离参数,然后数形结合求解,但是这个方法不见得是很恰当和很灵活的。
先变形为 a(1−x)=2+2lnx−2x,再分离参数为 a=2+2lnx−2x1−x,其中 x∈(0,12),
令函数 h(x)=2+2lnx−2x1−x,接下来用导数研究单调性,准备做函数的大值图像,
h′(x)=(2x−2)(1−x)−(2+2lnx−2x)(−1)(1−x)2=2lnx+2x−2(1−x)2
暂时没法看透 h′(x) 的正负值,也无法判断原函数 h(x) 的增减性,
故再设 h′(x) 的分子函数为 m(x)=2lnx+2x−2,
m′(x)=2x−2x2=2x−2x2,
由于 0<x<12,故 m′(x)<0,即 m(x) 单调递减,
故函数 m(x) 的最小值的极限为 m(12)=2ln12+4−2=2(1−ln2)>0
编外话:由分子函数 m(x) 的最小值的极限为正,说明函数 h′(x) 的分子都为正,
故 h′(x)=m(x)(1−x)2>0,故函数 h(x) 在 x∈(0,12) 上单调递增,
故 h(x) 的最大值的极限为 h(12)=2+2ln12−2×121−12=2(1−2ln2)
要使直线 y=a 与函数 y=h(x)(0<x<12) 没有交点,
则 a 的取值范围是 a≥2(1−2ln2),故 amin=2−4ln2。
【法 2】(分离参数,参数形式复杂,函数简单)
将原方程 (2−a)x−2(1+lnx)+a=0,先变形为 (2−a)x+(a−2)−2lnx=0,再变形为 2−a2=lnxx−1,
令 h(x)=lnxx−1,
则 h′(x)=1x(x−1)−lnx(x−1)2=1−1x−lnx(x−1)2
令 m(x)=1−1x−lnx,
则 m′(x)=1x2−1x=1−xx2>0 在 (0,12) 上恒成立,
故函数 m(x) 在 (0,12) 单调递增,
故 m(x)max 的极限为 m(12)=1−2−ln12=ln2−1<0
则函数 h′(x)=m(x)(x−1)2<0 在 (0,12) 上恒成立,
函数 h(x) 在 (0,12) 上单调递减,
则 h(x)min 的极限为 h(12)=ln1212−1=2ln2
要使得原方程无解,必须满足函数 y=2−a2 与函数 y=h(x) 没有交点,
即 2−a2≤2ln2,即 a≥2−4ln2
故 amin=2−4ln2。
【法 3】要是不用分离参数的方法,我们还可以这么分析呢?我们这样想,分离参数法是从数的角度来求解的,那么我们可以换个思路,想想能不能从形上入手分析?这时候,最好将原方程 f(x)=0 变形得到两个函数 h(x)=m(x),其中这两个函数最好是基本初等函数,这样它们的图像我们不用费事就能做出来,同时让参数配备个几何意义那是最好的选择,比如斜率等等,故求解如下:
由于函数 f(x)=0 在 x∈(0,12) 上没有零点,
则 (2−a)x−2(1+lnx)+a=0 在 x∈(0,12) 上没有零点,
变形为 (2−a)(x−1)=2lnx(0<x<12)
这样左端为函数 h(x)=(2−a)(x−1),是过定点 (1,0) 斜率是 2−a 的直线段,
右端为函数 m(x)=2lnx,是过定点 (1,0) 的对数型函数的一部分,图像
当直线段过点 (1,0) 和 (12,2ln12) 时,斜率为 k=2−2ln121−12=4ln2,
由图像可知,要让这两个定义在 x∈(0,12) 上的函数没有交点,
只需要函数 h(x) 的斜率 2−a 小于等于斜率 k=4ln2 即可,
故 2−a≤4ln2,即则 a 的取值范围是 a≥2(1−2ln2),
故 amin=2−4ln2。
解后反思:
1、法 1 是这类问题的通用解法,但是分离参数后得到的右端的函数,其单调性用导数判断可能很辛苦,这个题目就说明了这一点,而且用到了二阶导数,一般学生根本分不清一阶导数和二阶导数的关系,所以慎重使用。
2、法 2 比法 1 虽然都是分离参数法,但是我们感觉法 2 比法 1 要简单,其主要原因是法 2 采用的策略是,让函数简单些,让参数复杂些,这样运算量就小很多了。
3、法 3 将方程分离成立两个基本初等函数的形式,这样就可以很快很容易的使用形来解决问题了,到此我们也能体会命题人的意图,能将问题简化为我们学习过的,简单模型的学生,是不是其思维具有更好的可塑性。
通过以上七个方面的粗浅探索,相信各位会对分离参数法有更深入的理解,使用会更加得心应手。
对应练习
提示:选 C。
法 1:分别作出两个函数的图像,由图像可知 a⩾1,故选 C.
法 2:转化法,转化为函数 h(x)=f(x)−g(x)=x2−2lnx−a 有零点,分析单调性,令 h(x)min⩽0,故选 C.
法 3:转化法 + 分离参数法,转化为 a=x2−2lnx 有解,即函数 y=a 和函数 y=x2−2lnx 图像有交点,故选 C.
引申:可能还会同时考查整体思想,比如以下的题目;
函数 f(x)=x2,g(x)=2lnx+b2−b 有公共点,则 b 的取值范围是____________.
函数 f(x)=x2,g(x)=2lnx+a+1a 有公共点,则 a 的取值范围是____________.
思路补充
碰到函数有零点等问题时,我们一般优先选取分离参数法,但是如果分离后得到的函数的最值求解有难度或不太好分离参数时,次之选择分类讨论;
分析:当我们首选分离参数法时, a=x−√xlnx=h(x),接下来用导数求解 h(x) 的最值会非常麻烦,所以舍弃这个思路,采用分类讨论如下:
解析: 因为函数 f(x)=x−√x−alnx, 所以 f′(x)=1−12√x−ax=2x−√x−2a2x,
令 g(x)=2x−√x−2a, 因为 g′(x)=2−12√x=4√x−12√x
当 x∈(1,+∞) 时, 4√x−1>0,2√x>0, 所以 g′(x)>0,
所以 g(x) 在 (1,+∞) 上为增函数,则 g(x)>g(1)=1−2a,
当 1−2a⩾0 时, g(x)>0, 所以 f′(x)>0, 所以 f(x) 在 (1,+∞) 上为增函数,
则 f(x)>f(1)=0, 所以 f(x) 在 (1,+∞) 上没有零点;
当 1−2a<0 时, 即 a>12 时,因为 g(x) 在 (1,+∞) 上为增函数,
则存在唯一的 x0∈(1,+∞), 使得 g(x0)=0,
且当 x∈(1,x0) 时, g(x)<0, 当 x∈(x0,+∞) 时,g(x)>0;
所以当 x∈(1,x0) 时, f′(x)<0, f(x) 为减函数,
当 x∈(x0,+∞) 时 ,f′(x)>0, f(x) 为增函数,
当 x=x0 时,f(x)min=f(x0),
因为 f(x0)<f(1)=0, 当 x→+∞ 时,f(x)→+∞,
所以在 x∈(x0,+∞) 内, f(x) 一定存在唯一一个零点,
所以 a∈(12,+∞), 故选 D.
作者:陕西凤翔,微信:wh1979448597,邮箱:wanghai0666@126.com,敬请雅正,欢迎联系。
情怀:一直设想如何利用自己浅陋的教学感悟和粗鄙的电脑知识,将数学学习的手段和要素都整合到云端。
出处:https://www.cnblogs.com/wanghai0666/p/8617323.html
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。
题记:用数学的眼光观察世界,用数学的思维分析世界,用数学的语言表达世界!
声明:本博客版权归「静雅斋数学」所有。

 分离参数法,她和许多数学素材有关联,高三学生大多都耳熟能详,但对其具体的来由和需要注意的问题却不是很清楚。
分离参数法,她和许多数学素材有关联,高三学生大多都耳熟能详,但对其具体的来由和需要注意的问题却不是很清楚。
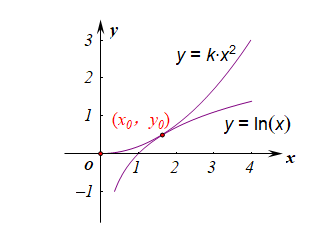



【推荐】国内首个 AI IDE,深度理解中文开发场景,立即下载体验 Trae
【推荐】编程新体验,更懂你的 AI,立即体验豆包 MarsCode 编程助手
【推荐】抖音旗下 AI 助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)