不等式性质使用中的易错题
前言
求二元函数的和差的取值范围或者积商的取值范围。
不等式性质
- 注意:求解\(x-y\)类的范围,其实是用\(x\)加上\(-y\)的范围得到的;
比如,已知\(-1\leqslant x\leqslant 4\),\(2\leqslant y\leqslant 3\),则\(x-y\)的取值范围是\([-4,2]\);\(3x+2y\)的取值范围是\([1,18]\);
- 注意:求解\(\cfrac{a}{b}\)的范围,其实是用\(a\)的范围乘以\(\cfrac{1}{b}\)的范围得到的;
比如,已知实数\(a\in (1,3)\),\(b\in (\cfrac{1}{8},\cfrac{1}{4})\),则\(\cfrac{a}{b}\)的取值范围是\((4,24)\)
分析:\(4<\cfrac{1}{b}<8\),\(a\in (1,3)\),所以\(4<\cfrac{a}{b}<24\);
分析:仿上,可以计算得到 \(2a-b\) 的取值范围是 \([5,8]\),后半段易错;
先求得 \(-1<\cfrac{1}{b}<-\cfrac{1}{2}\),再求得 \(\cfrac{1}{2}<-\cfrac{1}{b}<1\),又由于 \(2<a<3\),
两个同向不等式相乘得到,\(1<-\cfrac{a}{b}<3\),故 \(-3<\cfrac{a}{b}<-1\),
典例剖析
- 已知二元函数的和差的范围,求其和差的范围;
【法1:错解】由\(\begin{cases}1\leqslant f(-1)\leqslant 2\\2\leqslant f(1)\leqslant 4\end{cases}\) 得到
利用不等式的性质,将①②式相加减,得到
所以\(6 \leqslant 4a \leqslant 12,-3\leqslant -2b \leqslant 0\),所以\(3 \leqslant 4a-2b \leqslant 12\),又由于\(f(-2)=4a-2b\),故
【错因分析01】:由 \(\cfrac{3}{2}\leqslant a \leqslant 3\), \(0\leqslant b \leqslant \cfrac{3}{2}\),两式相加,得到 \(\cfrac{3}{2}\leqslant a \leqslant \cfrac{9}{2}\),和已知条件 \(2\leqslant a+b \leqslant 4\) 发生矛盾,说明出现了错误;那么具体是哪里出错了呢?
我们在学习不等式的性质时知道,\(\left\{\begin{array}{l}{a>b}\\{c>d}\end{array}\right.\) 是 \(a+c>b+d\) 的充分不必要条件,不是充要条件,即逆向推理不成立;也就是说,由 \(a+c>b+d\) 我们并不能得到 \(\left\{\begin{array}{l}{a>b}\\{c>d}\end{array}\right.\) .
我们用具体数字举例说明, \(\left\{\begin{array}{l}{1\leqslant a\leqslant 2}\\{3\leqslant b\leqslant 4}\end{array}\right.\) 可以得到 \(4\leqslant a+b\leqslant 6\) ,但是由 \(4\leqslant a+b\leqslant 6\) 并不能得到 \(1\leqslant a\leqslant 2\) ,\(3\leqslant b\leqslant 4\),也许是 \(0\leqslant a\leqslant 1\) ,\(4\leqslant b\leqslant 5\),或者其他的情形。这说明,我们采用的算理是错误的。
【错因分析02】:以上的解法将 \(a+b\)、和 \(a-b\)这个整体中 \(a\)、\(b\) 取值的内在联系打破,导致它们的范围发生变化,如由\(\cfrac{3}{2}\leqslant a \leqslant 3\),\(0\leqslant b \leqslant \cfrac{3}{2}\),当我们取\(a=\cfrac{3}{2}\),\(b=\cfrac{3}{2}\)时,很明显\(a-b=0,a-b\notin [1,2]\),故只要解法中没有把\(a-b\),\(a+b\)当成一个整体对待的都是有问题的解法。
【法2:正解】待定系数法,令\(f(-2)=mf(-1)+nf(1)\),
则由\(f(-2)=m(a-b)+n(a+b)=(m+n)a-(m-n)b\),
又由已知可知\(f(-2)=4a-2b\)
所以由对应系数相等得到方程\(\begin{cases} m+n=4 \\ m-n=2 \end{cases}\)
解得\(m=3,n=1\)
又由于\(1\leqslant f(-1)\leqslant 2\),$ 2\leqslant f(1)\leqslant 4$,
所以\(3\leqslant 3\cdot f(-1)\leqslant 6\),\(2\leqslant 1\cdot f(1)\leqslant 4\),
故\(5\leqslant 3\cdot f(-1)+1\cdot f(1)\leqslant 10\),
即\(5\leqslant f(-2)=4a-2b \leqslant 10\)。
【法3:正解】:方程组法
由已知有\(\begin{cases} f(-1)=a-b \\ f(\,\,\,\,1)=a+b \end{cases}\),解得\(\begin{cases} a=\cfrac{1}{2}\cdot [f(-1)+f(1)] \\ b=\cfrac{1}{2}\cdot [f(1)- f(-1)] \end{cases}\)
所以\(f(-2)=4a-2b=3f(-1)+f(1)\),
又由于\(1\leqslant f(-1)\leqslant 2\),\(2\leqslant f(1)\leqslant 4\),
所以\(3\leqslant 3\cdot f(-1)\leqslant 6\),\(2\leqslant 1\cdot f(1)\leqslant 4\),
故\(5\leqslant 3\cdot f(-1)+1\cdot f(1)\leqslant 10\),
即\(5\leqslant f(-2)=4a-2b \leqslant 10\)
【法4:正解】:线性规划法,用线性规划分析错误原因:
解法1中得到单个的\(a、b\)的取值范围是\(\cfrac{3}{2}\leqslant a \leqslant 3\)和\(0\leqslant b \leqslant \cfrac{3}{2}\),
由此作图得到的是矩形\(EFGH\),由条件\(1\leqslant f(-1)\leqslant 2\),\(2\leqslant f(1)\leqslant 4\)得到的是矩形\(ABCD\),
很显然两个矩形不一样,那么那个图形是对的?

我们可以看到在\(\Delta ADH\)内部的点,由线性规划知识可知并不满足条件\(1\leqslant a-b\leqslant 2\),\(2\leqslant a+b\leqslant 4\),
因此得到单个的\(a、b\)的取值范围是\(\cfrac{3}{2}\leqslant a \leqslant 3\)和\(0\leqslant b \leqslant \cfrac{3}{2}\)是错的,显然扩大了单个\(a、b\)的取值范围。
正解分析:由线性规划可知,
当直线\(l_0:4x-2y=0\)经过点\(A(\cfrac{3}{2},\cfrac{1}{2})\)时,
\(z=4x-2y\)有最小值,且\(z_{min}=4\times\cfrac{3}{2}-2\times\cfrac{1}{2}=5\);

当直线\(l_0:4x-2y=0\)经过点\(C(3,1)\)时,
\(z=4x-2y\)有最大值,且\(z_{max}=4\times3-2\times1=10\);
- 已知二元函数的积商的范围,求其积商的范围;
【法1】:类比上例中的法3
\(\because 1\leqslant lgxy \leqslant 2,\therefore 10\leqslant xy \leqslant 10^2,\)
又\(\because 3\leqslant lg\cfrac{x}{y} \leqslant 4,\therefore 10^3\leqslant \cfrac{x}{y} \leqslant 10^4,\)
\(10^3\leqslant (xy)^3 \leqslant 10^6,10^3\leqslant \cfrac{x}{y} \leqslant 10^4,\)
\(10^6\leqslant x^3\cdot y^3 \cdot \cfrac{x}{y} =x^4\cdot y^2 \leqslant 10^{10},\)
\(6\leqslant lg(x^4y^2) \leqslant 10\) ;
【法2】:类比上例中的法2
\(1\leqslant lgxy \leqslant 2\),\(3\leqslant lg\cfrac{x}{y} \leqslant 4,\)
\(1\leqslant lgx+lgy \leqslant 2\),\(3\leqslant lgx-lgy \leqslant 4,\)
仿照上例中的解法2,求得恰当的系数,可得
\(3\leqslant 3lgx+3lgy \leqslant 6\),\(3\leqslant lgx-lgy \leqslant 4,\)
所以同向不等式相加得到
\(6\leqslant 3lgx+3lgy+lgx-lgy \leqslant 10\)
即\(6\leqslant 4lgx+2lgy=lg(x^4y^2) \leqslant 10\)
\(6\leqslant lg(x^4y^2) \leqslant 10\)
【解后反思】之所以将这两个例题放在一起,是因为例1中涉及到两个变量的加减运算,而例2中涉及两个变量的乘除运算。
分析:①已知条件等价转化为不等式组\(\left\{\begin{array}{l}{-\cfrac{\pi}{2}<\alpha<\cfrac{\pi}{2} }\\{ -\cfrac{\pi}{2}<\beta<\cfrac{\pi}{2} }\\{ \alpha<\beta }\end{array}\right.\),
这样得到\(-\pi<\alpha-\beta<\pi\),且\(\alpha-\beta<0\),故\(-\pi<\alpha-\beta<0\),
②仿上,先转化得到\(-\pi<\alpha-\beta<0\),又由于\(-\cfrac{\pi}{2}<\alpha<\cfrac{\pi}{2}\),
两个同向不等式相加,得到\(-\cfrac{3\pi}{2}<2\alpha-\beta<\cfrac{\pi}{2}\),
法1:[错解]由题知\(\begin{cases} \Delta \ge 0 \\ x_1+x_2>2 \\ x_1\cdot x_2>1 \end{cases}\),错在不等式性质的应用上,
- 相关链接:不等式性质
同向不等式的可加性:\(\begin{cases}a>b\\c>d\end{cases}\)是\(a+c>b+d\)的充分不必要条件,
也就是说由\(\begin{cases}x_1+x_2>2\\x_1\cdot x_2>1\end{cases}\)并不能推出本题想要的结果\(\begin{cases}x_1>1\\x_2>1\end{cases}\),
故这样的解集必然是错误的。
不过我们注意到\(\begin{cases}a+b>0\\ab>0\end{cases}\)等价于\(\begin{cases}a>0\\b>0\end{cases}\),
那么把上面的解法稍微做个改进就得到法2:
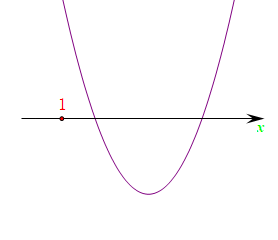
法2: 分析,变形使用不等式的性质,得到\(\begin{cases} \Delta \ge 0 \\ x_1+x_2>2 \\ (x_1-1)\cdot (x_2-1)>0 \end{cases}\)
法3: 分析,有对应的函数图像转化得到不等式组,\(\begin{cases} \Delta \ge 0 \\ -\cfrac{m-1}{2}>1 \\ f(1)>0 \end{cases}\)

 收集整理不等式性质使用中的易错题目,分析出错原因,提出避免错误的方法。
收集整理不等式性质使用中的易错题目,分析出错原因,提出避免错误的方法。
