斐波那契数列

公式定理💯随心记

【双曲线的标准方程】文字语言：平面内到两个定点 $F_1,F_2$ 的距离之差的绝对值等于常数（小于 $|F_1F_2|$）的点的轨迹。符号语言：标准方程 $\cfrac {x^2}{a^2}-\cfrac {y^2}{b^2}=1$$(a>0,b>0)$，其中 $c^2=a^2+b^2$；渐近线 $y=\pm\cfrac {b}{a} x$；离心率 $e=\cfrac {c}{a}>1$

---

前情概要

斐波那契数列又称黄金分割数列，因数学家列昂纳多・斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为 “兔子数列”，指的是数列 $1$ , $1$ , $2$ , $3$ , $5$ , $8$ , $13$ , $\cdots$，在数学上，斐波纳契数列以递归的方法定义 $a_1=1$，$a_2=1$，且满足 $a_{n+1}$ $=$ $a_n$ $+$ $a_{n-1}$，$n$ $\geqslant$ $2$；^[1]

图象绘制

通项公式

• 斐波那契数列 $\{a_n\}$ 的递推关系式满足条件：$a_n=\left\{\begin{array}{l}1,&n=1\\1,&n=2\\a_{n-1}+a_{n-2},&n\geq 3\end{array}\right.$，其通项公式如下：

$$a_n=\cfrac{1}{\sqrt{5}}\bigg[(\cfrac{1+\sqrt{5}}{2})^n-(\cfrac{1-\sqrt{5}}{2})^n\bigg]$$

详细求解过程，请参阅斐波那契数列通项公式的求解

黄金分割比

斐波那契数列与黄金分割比，直接给结论：斐波那契数列相邻项比值的极限是 $0.618$，意思就是随着斐波那契数列越来越大，相邻两项的比值越来越接近 $0.618$，证明也非常简单，只要有大学高数的极限知识即可 。

由于 $a_{n+2}=a_{n+1}+a_{n}$，两边同除以 $a_{n+1}$，得到

$\cfrac{a_{n+2}}{a_{n+1}}=1+\cfrac{a_{n}}{a_{n+1}}\;\;(\ast)$，假设其极限存在，令其为 $Q$，

由于 $\lim\limits_{n\rightarrow \infty}\cfrac{a_{n+2}}{a_{n+1}}=Q$， $\lim\limits_{n\rightarrow \infty}\cfrac{a_{n+1}}{a_{n}}=Q$，

所以 $(\ast)$ 式 等价于 $Q=1+\cfrac{1}{Q}$，

解得，$Q=\cfrac{1\pm\sqrt{5}}{2}$，舍去负值，则 $\cfrac{1}{Q}=\cfrac{2}{1+\sqrt{5}}=\cfrac{\sqrt{5}-1}{2}$$\approx 0.618$ .

即斐波那契数列相邻项比值 [后项与相邻前项之比] 的极限是 $0.618$ .

http://www.matrix67.com/blog/archives/5221

典例剖析

【2024 新课标全国 Ⅰ 卷第 8 题】已知函数 $f(x)$ 的定义域为 $R$，$f(x)$$>$$f(x-1)$$+$$f(x-2)$，且当 $x$$<$$3$ 时 $f(x)$$=$$x$，则下列结论中一定正确的是【$\qquad$】

$A.f(10) > 100$ $B.f(20) > 1000$ $C.f(10) < 1000$ $D.f(20) < 10000$

解法 1️⃣：【学科网的解答方法】因为当 $x<3$ 时， $f(x)=x$，所以 $f(1)=1$，$f(2)=2$，又因为 $f(x)$$>$$f(x-1)$$+$$f(x-2)$，

则 $f(3)$$>$$f(2)$$+$$f(1)$$=$$3$，$f(4)$$>$$f(3)$$+$$f(2)$$>$$5$，

$f(5)$$>$$f(4)$$+$$f(3)$$>$$8$， $f(6)$$>$$f(5)$$+$$f(4)$$>$$13$， $f(7)$$>$$f(6)$$+$$f(5)$$>$$21$，

$f(8)$$>$$f(7)$$+$$f(6)$$>$$34$， $f(9)$$>$$f(8)$$+$$f(7)$$>$$55$， $f(10)$$>$$f(9)$$+$$f(8)$$>$$89$，

$f(11)$$>$$f(10)$$+$$f(9)$$>$$144$，$f(12)$$>$$f(11)$$+$$f(10)$$>$$233$，$f(13)$$>$$f(12)$$+$$f(11)$$>$$377$

$f(14)$$>$$f(13)$$+$$f(12)$$>$$610$，$f(15)$$>$$f(14)$$+$$f(13)$$>$$987$，

$f(16)$$>$$f(15)$$+$$f(14)$$>$$1597$$>$$1000$，则依次下去可知 $f(20)$$>$$1000$，则 $B$ 正确；且无证据表明 $ACD$ 一定正确，故选: $B$.

解法 2️⃣：如果对斐波那契数列比较熟悉的话，由 $x$$<$$3$ 时 $f(x)$$=$$x$，得到 $f(1)=1$，$f(2)=2$，且 $f(x)$$>$$f(x-1)$$+$$f(x-2)$，将其中的 > 改为 =，则所考查的就是斐波那契数列的相关知识，由已知条件我们可以自行写出下面的数列 [斐波那契数列的一部分，没有第一项]：

$1$,$2$,$3$,$5$,$8$,$13$,$21$,$34$,$55$,$89$,$144$,$233$,$377$,$610$,$987$,$1597$,$2584$,$4181$,$6765$,$10964$,$17711$,

再将上述的斐波那契数列的部分数列，将其中的 = 改为 >，即

$1$,$2$,$f(3)>3$,$f(4)>5$,$f(5)>8$,$f(6)>13$,$f(7)>21$,$f(8)>34$,$f(9)>55$,$f(10)>89$,$f(11)>144$,$f(12)>233$,$f(13)>377$,$f(14)>610$,$f(15)>987$,$f(16)>1597$,$f(17)>2584$,$f(18)>4181$,$f(19)>6765$,$f(20)>10964$,$f(21)>17711$,

这样能很容易的判断，选项 $AD$ 是错误的，选项 $B$ 是一定正确的，选项 $C$ 的正误不好判断，由于是单选题，对比之下，只能选 $B$ .

【与斐波那契数列有关的归纳推理】某种树的分枝生长规律如图所示，第 1 年到第 5 年的分枝数分别为 $1$，$1$，$2$，$3$，$5$，则预计第 10 年树的分枝数为【$\qquad$】

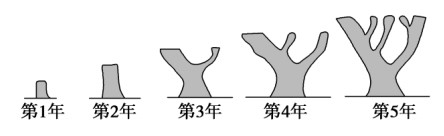
$A.21$ $B.34$ $C.52$ $D.55$

分析：本题目涉及到的数列为 “斐波那契数列”，其构成规律为：$a_1=1$，$a_2=1$ 已知，其他项由递推公式 $a_{n+2}$$=$$a_{n+1}$$+$$a_n$，$n\in N^*$ 得到，

故 $a_6=8$，$a_7=13$，$a_8=21$，$a_9=34$，$a_{10}=55$，$a_{11}=89$，故选 $D$。

【2021$\cdot$ 上海模拟】著名的斐波那契数列 $\{a_{n}\}$: $1$，$1$，$2$，$3$，$5$，$8$， $\cdots$， 满足 $a_{1}$$=$$a_{2}$$=$$1$， $a_{n+2}$$=$$a_{n+1}$$+$$a_{n}$$(n\in {N}^{*})$，那么 $1$$+$$a_{3}$$+$$a_{5}$$+$$a_{7}$$+$$a_{9}$$+$$\cdots$$+$$a_{2021}$ 是斐波那契数列中的第【$\quad$】项

$A.2020$ $B.2021$ $C.2022$ $D.2023$

解析： 因为 $a_{1}$$=$$a_{2}$$=$$1$ ，所以

$1$$+$$a_{3}$$+$$a_{5}$$+$$a_{7}$$+$$a_{9}$$+$$\cdots$$+$$a_{2021}$

$=$$a_{2}$$+$$a_{3}$$+$$a_{5}$$+$$a_{7}$$+$$a_{9}$$+$$\cdots$$+$$a_{2021}$

$=$$a_{4}$$+$$a_{5}$$+$$a_{7}$$+$$a_{9}$$+$$\cdots$$+$$a_{2021}$

$=$$a_{6}$$+$$a_{7}$$+$$a_{9}$$+$$\cdots$$+$$a_{2021}$

$=$$\cdots$$+$$a_{2019}$$+$$a_{2021}$

$=$$a_{2020}$$+$$a_{2021}$$=$$a_{2022}$ ，故选 $C$ .

相关延申

函数的周期，$f(x+2)=f(x+1)-f(x)$，求周期；

---

1. 斐波那契数列的通项公式的推导过程 ↩︎