多个参数之和积的取值范围 02
💎更新于 2025-03-04 17:48 | 发布于 2024-11-04 20:27
约 13721 字 | 阅读估时 46 分钟
前情概要
本博文是从多个参数之和积的取值范围 01 中分离出来的,想让学生一看到标题就知道其内容,但是实在不知道起个什么名字合适,暂时还用这个名字吧,其实解决的问题是类似于已知 f(a)=f(b)=f(c)f(a)=f(b)=f(c),而求解 x1+x2+x3+x4x1+x2+x3+x4 之类的取值范围的问题。要是细细分析还是涉及函数性质的综合应用的。
常用结论
✍️ 已知函数 f(x)=|2x−1|f(x)=|2x−1|,若互异的实数 aa,bb 满足方程 f(a)=f(b)f(a)=f(b),则 2a+2b=22a+2b=2。
✍️ 已知函数 f(x)=|lgx|f(x)=|lgx|,若互异的实数 aa,bb 满足方程 f(a)=f(b)f(a)=f(b),则 ab=1ab=1。
✍️ 已知函数 f(x)=|lnx−1|f(x)=|lnx−1|,若互异的实数 aa,bb 满足方程 f(a)=f(b)f(a)=f(b),则 ab=e2ab=e2。
✍️ 已知函数 f(x)=|x−1|f(x)=|x−1|,若互异的实数 aa,bb 满足方程 f(a)=f(b)f(a)=f(b),则 a+b=2a+b=2。
✍️ 已知函数 f(x)=|ln(x−1)|−mf(x)=|ln(x−1)|−m,若互异的实数 aa,bb 满足方程 f(a)=f(b)f(a)=f(b),则 ab=a+bab=a+b。
✍️ 已知函数 f(x)=x+1xf(x)=x+1x,若互异的实数 aa,bb 满足方程 f(a)=f(b)f(a)=f(b),则 ab=1ab=1。
✍️ 已知函数 f(x)=|1−1x|f(x)=|1−1x| (x>0)(x>0),若 0<a<b0<a<b 且满足方程 f(a)=f(b)f(a)=f(b),则 1a+1b=21a+1b=2。
- 以上常用的结论需要各位理解并记忆,具体推理过程,请参阅 多个参数之和积的取值范围 01,在此不再赘述 .
典例剖析
解析:做出图象,由图可知,左边的二次函数对称轴为 x=−2x=−2,故可以得到 x1+x2=−4x1+x2=−4;又由于 f(x3)=f(x4)f(x3)=f(x4),且有 0<x3<2<x40<x3<2<x4,则 |lnx3|=|lnx4||lnx3|=|lnx4|,即 −lnx3=lnx4−lnx3=lnx4,则 lnx3+lnx4=0lnx3+lnx4=0,由此得到,x3⋅x4=1x3⋅x4=1,这些由上述的数学常识页可以快速得到。
由动态图象可知,0<a⩽20<a⩽2,故选项 BB 正确,当 a=2a=2 时,x1=−4x1=−4,x2=0x2=0,x3=e−2x3=e−2,x4=e2x4=e2,故选项 AA,DD 错误,当将动态的直线从 y=0y=0 的位置拉到 y=2y=2 的位置,可知 2<x3+x4≤e2+1e22<x3+x4≤e2+1e2,故选项 CC 正确,综上,选 BCBC .
本题目做记录的用意,是为了防止这样的错误【高频易错】:将动态直线从 y=0y=0 拉到 y=2y=2 的位置过程中,可知单独的参数 1e21e2⩽⩽x3x3<<11,11<<x4x4⩽⩽e2e2,这样的表达是正确的,但是若要计算 x3x3++x4x4 的范围,却不能使用刚才的同向不等式相加得到,即 11++1e21e2<<x3x3++x4x4<<11++e2e2 是错误的,原因是她们变化过程中必须时刻满足 x3x3⋅⋅x4x4==11,故 x3x3++x4x4 的最小值极限为 11++11==22,最大值为 e2e2++1e21e2,故选项 CC 是正确的,同样的例子还有,−1−1⩽⩽sinθsinθ⩽⩽11,−1−1⩽⩽cosθcosθ⩽⩽11,都是正确的,但是 −2−2⩽⩽sinθsinθ++cosθcosθ⩽⩽22 却是错误的,原因是她们必须始终满足条件 sin2θsin2θ++cos2θcos2θ==11,心里清楚的学生到此已经知道,sinθsinθ++cosθcosθ==√2√2sin(θ+π4)sin(θ+π4),故应该是 −√2−√2⩽⩽sinθsinθ++cosθcosθ⩽⩽√2√2 . 关联阅读辅助角公式 和 换元法;
解析:而言,由题意可知 2x1+2x1=52x1+2x1=5①, 2x2+2log2(x2−1)=52x2+2log2(x2−1)=5②,
由①式可得 2x1=5−2x12x1=5−2x1,则指数式化为对数式得到 x1=log2(5−2x1)x1=log2(5−2x1),
即 2x1=2log2(5−2x1)2x1=2log2(5−2x1), 令 2x1=7−2t2x1=7−2t 此处的变形技巧性很强,为什么这样设元,原因是既要照顾到 2x12x1,还要考虑变形后要和②式一模一样,故此处的操作技巧型太强了 ,
代入上式得 7−2t7−2t==2log2[5−(7−2t)]2log2[5−(7−2t)]
==2log2(2t−2)2log2(2t−2)==2[1+log2(t−1)]2[1+log2(t−1)]==2+2log2(t−1)2+2log2(t−1),
则 5−2t=2log2(t−1)5−2t=2log2(t−1),即 2t+2log2(t−1)=52t+2log2(t−1)=5, 与②式比照得到 t=x2t=x2,
于是 2x1=7−2x22x1=7−2x2,即 x1+x2=3.5x1+x2=3.5,
解析:首先做出函数 y=f(x)y=f(x) 的图像,注意分段函数 y=x⋅lnxy=x⋅lnx 的图像的做法;用导数判断其单调性,在 (0,1e](0,1e] 上单调递减,在 [1e,+∞)[1e,+∞) 上单调递增,用方程 x⋅lnx=0x⋅lnx=0 求解函数的零点 x=0x=0 和 x=1x=1;
则直线 y=ky=k 和函数 y=f(x)y=f(x) 的交点的横坐标分别为 x1x1 和 x2x2 ,
则原问题转化为求线段 |x1x2||x1x2| 的长度的最大值 [视角 1];
由于直线 y=x+1y=x+1 的倾斜角为固定角 π4π4,
则可以将此距离转化为 x2x2 到直线 y=x+1y=x+1 的垂线段的长度 [视角 2] 的 √2√2 倍;
而此长度又可以转化为曲线 y=x⋅lnxy=x⋅lnx 上的动点到直线 y=x+1y=x+1 的距离的最大值,
从而和导数建立关联已经掌握的类型;
设斜率为 11 的直线 y=x+my=x+m 和曲线 y=x⋅lnxy=x⋅lnx 相切于点 P(x0,y0)P(x0,y0) ,
则由 lnx0+1=1lnx0+1=1,可得 x0=1x0=1 ,代入 y=x⋅lnxy=x⋅lnx 求得 y0=0y0=0 ,故切点为 (1,0)(1,0) ;
则点 (1,0)(1,0) 到直线 y=x+1y=x+1 的距离为 √2√2 ,故所求的距离为 √2×√2=2√2×√2=2 ,故选 CC.
解析: 作函数 f(x)={|x+1|,x⩽0,|log2x|,x>0,f(x)={|x+1|,x⩽0,|log2x|,x>0, 的图象如下,
由于函数 y=|x+1|y=|x+1| 关于直线 x=−1x=−1 对称,故由图可知, x1+x2=−2x1+x2=−2,
又由于 |log2x3|=|log2x4||log2x3|=|log2x4|,即 −log2x3=log2x4−log2x3=log2x4 ,即 log2(x3x4)=0=log21log2(x3x4)=0=log21,则 x3x4=1x3x4=1
故 x3(x1+x2)+1x23x4=−2x3+1x3x3(x1+x2)+1x23x4=−2x3+1x3,即所求转换为新函数 g(x3)=−2x3+1x3g(x3)=−2x3+1x3,
接下来需要确定函数的定义域,平移图中的直线,可以得到 0<|log2x3|⩽10<|log2x3|⩽1,
即 log21<−log2x3⩽log22log21<−log2x3⩽log22,解得 x3∈[12,1)x3∈[12,1),
到此,所求转化为求解函数 g(x3)=−2x3+1x3g(x3)=−2x3+1x3,x3∈[12,1)x3∈[12,1) 的值域问题;
由于函数 g(x3)g(x3) 在区间 [12,1)[12,1) 上是减函数,
故 −1<g(x3)⩽1−1<g(x3)⩽1,故选 BB.
解后反思:也有学生由图像能得到,x1<−1x1<−1,−1<x2⩽0−1<x2⩽0,0<x3<10<x3<1,x4>1x4>1,
但是这只是对函数的图像的表象的认知,对函数的本质的特性没有挖掘出来,比如对称性。
解法一: 方程 f(x)=kxf(x)=kx 可化为 x⋅f(x)=kx⋅f(x)=k,
令 g(x)=xf(x)g(x)=xf(x), 则 g(x)={x2−4x,x⩾4,−x2+4x,x<4.g(x)={x2−4x,x⩾4,−x2+4x,x<4.
作出 g(x)g(x) 的图象,如图所示, 方程 xf(x)=kxf(x)=k 有三个互不相等的实根 x1,x2,x3x1,x2,x3,
等价于函数 g(x)g(x) 的图象与直线 y=ky=k 有三个不同的交点,
结合图象可知 0<k<40<k<4, 不妨设 x1<x2<x3x1<x2<x3, 由图象可知 x3>4x3>4,
由二次函数 y=−x2+4xy=−x2+4x 的图象关于直线 x=2x=2 对称可知,x1+x22=2x1+x22=2,
即 x1+x2=4x1+x2=4,令 x2−4x=4x2−4x=4, 解得 x=2±2√2x=2±2√2, 所以 4<x3<2+2√24<x3<2+2√2,
所以 4+4<x1+x2+x3<4+2+2√24+4<x1+x2+x3<4+2+2√2,即 8<x1+x2+x3<6+2√28<x1+x2+x3<6+2√2,. 故选 DD.
解法二:直接利用题目给定的条件,拆分为函数 y=f(x)y=f(x) 和函数 y=kxy=kx 有三个不同的交点,如下图所示,
由图可知, 函数 y=kxy=kx 与 函数 y=−x+4(x<4)y=−x+4(x<4) 应该有两个交点 x1x1,x2x2(不妨令 x1<x2x1<x2 ),函数 y=kxy=kx 与 函数 y=x−4(x⩾4)y=x−4(x⩾4) 应该有一个交点 x3x3( x3>4x3>4 ),
由 f(x)={y=−x+4,x⩾4y=kx,x>0,k>0f(x)=⎧⎨⎩y=−x+4,x⩾4y=kx,x>0,k>0 可得到,
x2−4x+k=0x2−4x+k=0,则由韦达定理可知 x1+x2=4x1+x2=4,
且由 x2−4x+k=0x2−4x+k=0 可知, 当 k=4k=4 时,y=−x+4(x<4)y=−x+4(x<4) 和 y=kxy=kx 相切,
当 k>4k>4 时,y=−x+4(x<4)y=−x+4(x<4) 和 y=kxy=kx 相离,不满足有三个交点的情形,
当 0<k<40<k<4 时, y=−x+4(x<4)y=−x+4(x<4) 和 y=kxy=kx 有两个交点,y=x−4(x⩾4)y=x−4(x⩾4) 和 y=kxy=kx 有一个交点,满足题意;
在此动态变化过程中,可以看出 x3x3 的范围的下限为 44,其上限的求解,需要 k=4k=4,
从而联立 y=kxy=kx 和 y=x−4(x⩾4)y=x−4(x⩾4) 求解得到 x3=2+2√2x3=2+2√2(舍去 x3=2−2√2x3=2−2√2 ),
故得到 4<x3<2+2√24<x3<2+2√2,
所以 4+4<x1+x2+x3<4+2+2√24+4<x1+x2+x3<4+2+2√2,即 8<x1+x2+x3<6+2√28<x1+x2+x3<6+2√2,. 故选 D.
解后反思:在由数转化为形的过程中,我们有两个变形的思路:其一,[首先想到,也最容易想到的] 直接利用题目给定的条件,拆分为函数 y=f(x) 和函数 y=kx 有三个不同的交点;其二,先转化为方程 xf(x)=k 有三个互不相等的实根 x1,x2, x3,再转化为利用形来求解,相比而言,明显此思路要更先进一些,思维的层次就更高一些,作图也便利,还能利用函数的对称性。
解析:函数 f(x) 的图象如图所示, 易知 x3+x42=3,则 x3+x4=6,
又 −log2x1=log2x2, 所以 log2(x1x2)=0, 即 x1x2=1,
所以 x1x2(x3+x4)=6 .
解析:由于函数要有四个不同的零点,则必须 a>0,由于函数 f(x)=x2+2x−a 的对称轴为 x=−1,故 x1+x2=−2,
另外,参照相关例题解法可知,x3x4=x3+x4,故 x1−x3+x2−x4+x3x4=−2,
故选 D . 对应课件
【法 1】:函数 f(x) 的零点问题,转化为函数 y=|2x−1| 与 y=k 的图像交点的横坐标问题,同理,函数 g(x) 的零点问题,转化为函数 y=|2x−1| 与 y=k2k+1 的图像交点的横坐标问题,
又由于 y=k2k+1=12+1k,在 k∈[13,1) 上单调递增,即当 k 的取值从 13 增大到 1 时,k2k+1 的取值对应的从 15 增大到 13,
做出如下的图像,从图像入手分析,当 y=k 向上平移时,x2−x1 逐渐增大,同理对应的 x4−x3 逐渐增大,所以要使得 x4+x2−(x3+x1) 取到最小值,则需要 x4−x3 和 x2−x1 同时取到最小值,此时 k=13,同时对应的有 k2k+1=15;
此时,|2x2−1|=13,即 2x2−1=13,解得 x2=log243,又 |2x1−1|=13,即 1−2x1=13,解得 x1=log223,
同理对应的有 |2x4−1|=15,即 2x4−1=15,解得 x4=log265,又 |2x3−1|=15,即 1−2x3=15,解得 x3=log245,
故此时 [x4+x2−(x3+x1)]min=(log265−log245)+(log243−log223)=log23,故选 B。
【法 2】:由题可知,2x2−1=k,1−2x1=k,
故有 2x2=k+1,2x1=1−k,则 2x2−x1=1+k1−k;
同理,2x4=1+k2k+1=3k+12k+1,2x3=1−k2k+1=k+12k+1,
则 2x4−x3=3k+1k+1;则 2x4−x3⋅2x2−x1=3k+1k+1⋅1+k1−k=3k+11−k,
又 3k+11−k=−(−3k+3)+41−k=−3+41−k,
由于 13≤k<1,则 0<1−k≤23,则 41−k≥6,则 −3+41−k≥3,
即 2(x4−x3)+(x2−x1)≥3,则 (x4−x3)+(x2−x1)≥log23,故选 B。
解后反思:1、本题目还可以使用直接求解的方法,待后补充;比如 2x1+2x2=2;
则可以得到 2≥2⋅√2x1⋅2x2;则 √2x1+x2≤1,即 2x1+x2≤1,则 x1+x2≤0;
2、比如将条件更改为 13≤k≤45,那么用相应的思路和方法,可以求解 x4+x2−(x3+x1) 的取值范围;
分析:做出示意图如下所示,
由图可知,x1∈(0,1),x2∈(1,2),又由 f(x1)=f(x2),即 |log2x1|=|log2x2|,
即 −log2x1=log2x2,即 log2x1+log2x2=0,则 log2x1x2=0,即 x1x2=1;
又第二段函数图像关于直线 x=6 对称,即 x3,x4 关于直线 x=6 对称,
故有 x3+x4=2×6=12;故 x3+x4x1x2=12;
分析:做出函数的图像,不妨设从左到右的五个实数根依次为是 x1, x2,x3, x4,x5,由图像可知,
x1 和 x2 关于直线 x=−π2 对称, x3 和 x4 关于直线 x=π2 对称,则 x1+x2+x3+x4=0,
且 π<x5<10,故 x1+x2+x3+x4+x5∈(π,10),故选 B.
法 1:自行做出函数的图像,由 m>n>1 可知,f(m)=|m2−2m−1|=m2−2m−1,
f(n)=|n2−2n−1|=−n2+2n+1,
又由于 f(m)=f(n),则 m2−2m−1=−n2+2n+1,
即 m2+n2−2m−2n−2=0,即 (m−1)2+(n−1)2=4=22,
则 m=1+2cosθ,n=1+2sinθ,θ∈(0,π4),
[对角 θ 范围的说明:由 m>n>1,得到 1+2cosθ>1+2sinθ>1,即 cosθ>sinθ>0,故 0<θ<π4]
则 mn=(1+2cosθ)(1+2sinθ)=1+2(cosθ+sinθ)+4sinθcosθ
令 t=sinθ+cosθ,则 2sinθcosθ=t2−1
且 t=sinθ+cosθ=√2sin(θ+π4)∈(1,√2),
所以 mn=2t2+2t−1=g(t),t∈(1,√2),
当 t=1 时,mn 的最小值的极限,即 g(t) 最小值的极限为 g(1)=3,
当 t=√2 时,mn 的最大值的极限,即 g(t) 最大值的极限为 g(√2)=3+2√2,
故 mn∈(3,3+2√2),故选 A;
法 2:用图形说明,由上述的动图,我们容易知道 1<n<1+√2,1+√2<m<3,
但是由同向不等式性质,得到 1×(1+√2)<mn<3×(1+√2) 却是错误的,
[原因是所作的直线始终要和 x 轴平行,故 n→1 时,m→3,而不是 m→1+√2]
如果要用乘法,也应该是 1×3 和 (1+√2)×(1+√2)=3+2√2
但是这个做法有凑答案之嫌,故最合理的做法是上述的法 1;
解后反思:深入思考法 1 的解法,我们发现本题目还可以用来做这样的考查;
①求 m+n 的取值范围;
②求 (m−1)(n−1) 的取值范围;
解:由题意可得 x1 是函数 y=log4x 的图象和 y=(14)x 的图象的交点的横坐标,
x2 是函数 y=log14x 的图象和 y=(14)x 的图象的交点的横坐标,
且 x1, x2 都是正实数,且 0<x2<1,x1>1,如图所示,
由图可知,有 (14)x2>(14)x1
故 log14x2−log4x1>0,即 −log4x2−log4x1>0,则 log4x1+log4x2<0,
log4(x1⋅x2)<0, 则 0<x1⋅x2<1, 故选 B.
作者:陕西凤翔,微信:wh1979448597,邮箱:wanghai0666@126.com,敬请雅正,欢迎联系。
情怀:一直设想如何利用自己浅陋的教学感悟和粗鄙的电脑知识,将数学学习的手段和要素都整合到云端。
出处:https://www.cnblogs.com/wanghai0666/p/18526101
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。
题记:用数学的眼光观察世界,用数学的思维分析世界,用数学的语言表达世界!
声明:本博客版权归「静雅斋数学」所有。

 收集整理形如已知
收集整理形如已知 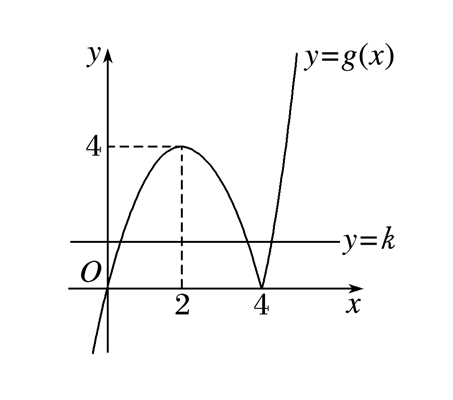



【推荐】国内首个 AI IDE,深度理解中文开发场景,立即下载体验 Trae
【推荐】编程新体验,更懂你的 AI,立即体验豆包 MarsCode 编程助手
【推荐】抖音旗下 AI 助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架
2017-11-04 多个参数之和积的取值范围01