前情概要
如果没有笛卡尔平面直角坐标系,那么涉及平面向量的问题只能用基向量的方法 [形的角度] 求解,不能用代数方法 [数的角度] 计算;同理如果没有空间直角坐标系的介入,立体几何中的问题也就只能从形的角度思考,而不能用代数方法 [数的角度] 来计算;所以建系的目的主要是想把有关形的问题,通过代数的方法计算解决;
本博文旨在总结立体几何中常见几何体的建系方法和类型,比如正四面体中、正三棱柱中、四棱锥等中的建系方法,坐标计算方法等,便于学习。而且我们应该知道,当建立的坐标系不同时,计算的难度是不一样的。
建系汇总
- 平面问题中若涉及平面向量的计算问题,常可以建立平面直角坐标系;
【2017 河北武邑中学一模,文 11】在 Rt△ABC 中,CA=CB=3,M,N 是斜边 AB 上的两个动点,MN = √2,则 −−→CM⋅−−→CN 的取值范围是【】
A.[2,52] B.[2,4] C.[3,6] D.[4,6]
分析:求向量的内积的取值范围,应该想到用内积的坐标运算,本题目难点是一般想不到主动建系,由形的运算转化为数的运算。
解:如图所示,以点 C 为坐标原点,分别以 CB、CA 所在的直线为 x、y 轴建立如同所示的坐标系,则 C(0,0),A(0,3),B(3,0),设点 N 的横坐标为 x,则由等腰直角三角形可知,点 N 的纵坐标为 3−x,即点 N(x,3−x),
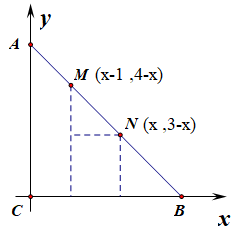
又由 MN=√2,计算可知点 M(x−1,4−x),则 −−→CM=(x−1,4−x),−−→CN=(x,3−x),
由于点 M,N 是动点,取两个极限位置研究 x 的取值范围,
当点 M 位于点 A 时,x 取到最小值 1,当点 N 位于点 B 时,x 取到最大值 3,即 1≤x≤3,
则 −−→CM⋅−−→CN=f(x)=(x−1,4−x)⋅(x,3−x)
=x(x−1)+(4−x)(3−x)=2(x−2)2+4,x∈[1,3]
当 x=2 时,f(x)min=f(2)=4,当 x=1 或 x=3 时,f(x)max=f(1)=f(3)=6,
即 f(x)∈[4,6]。故选 D。
【解后反思】对于以图形为背景的向量数量积运算的题目,只需把握图形的特征,建立适当的平面直角坐标系,写出相应点的坐标即可求解。
【2019 届高三理科数学三轮模拟试题】如图,已知两点 A,B 在单位圆上,∠yOB=60∘,∠xOA=30∘,则 |2−−→OA+3−−→OB|=___________。
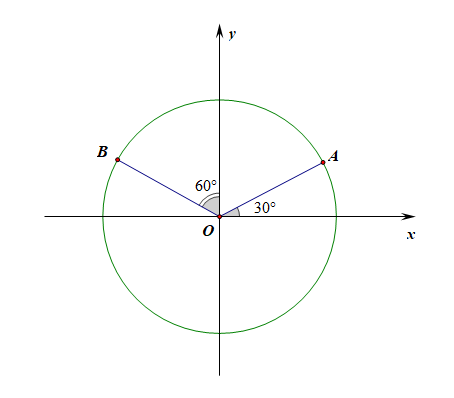
解法 1️⃣ :坐标法,已知 A(√32,12),B(−√32,12),则 −−→OA=(√32,12),
−−→OB=(−√32,12),则 2−−→OA+3−−→OB=(−√32,52),
故 |2−−→OA+3−−→OB|=√(−√32)2+(52)2=√7。
解法 2️⃣:向量法,由题目可知,∠AOB=120∘,|−−→OA|=|−−→OB|=1,
则 |2−−→OA+3−−→OB|=√|2−−→OA+3−−→OB|2
=√4|−−→OA|2+9|−−→OB|2+2×2×3×−−→OA⋅−−→OB
=√4+9+2×2×3×1×1×(−12)=7,故 |2−−→OA+3−−→OB|=√7。
解法 3️⃣ :解三角形法,由向量的平行四边形法则可知,所求的模长即 △OCD 中的边长 |OC|,由已知 |OD|=3|OB|=3,|CD|=2|OA|=2,∠ODC=60∘,
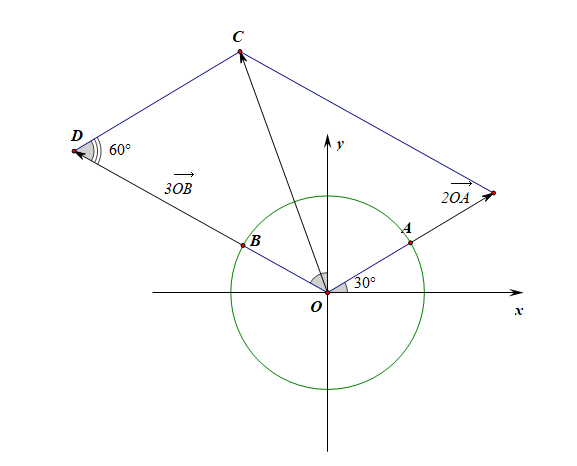
由余弦定理可知 |2−−→OA+3−−→OB|2=|OC|2=22+32−2×2×3×cos60∘=7,
故 |2−−→OA+3−−→OB|=√7。
【2019 届高三理科数学二轮用题】在矩形 ABCD 中,AB=2,AD=4,AC 与 BD 相交于点 O,过点 A 作 AE⊥BD 于 E,则 −−→AE⋅−−→AC=【】
A.85 B.165 C.325 D.8
解法 1️⃣ :从形的角度思考,采用坐标法求解;以点 A 为坐标原点建立如图所示的直角坐标系,
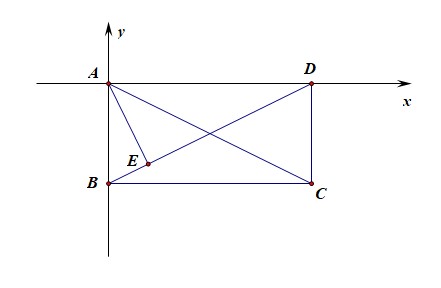
则可知 A(0,0),B(0,−2),C(4,−2),D(4,0),设 E(x,y),
则由 kAE⋅kBD=−1,可得 y=−2x①,又直线 BD:2y=x−4②,
联立①②可得,x=45,y=−85,
则 −−→AE⋅−−→AC=(45,−85)⋅(4,−2)=325,故选 C .
解法 2️⃣ :本题目还可以用基向量法,以 −−→AB 和 −−→AD 为基向量来表示其他向量,
由射影定理可知,AB2=BE⋅BD,又 BD=2√5,故 BE=2√55,
令 −−→BE=t−−→BD,则 t=|−−→BE||−−→BD|=15,
又 −−→AE=−−→AB+−−→BE=−−→AB+15−−→BD
=−−→AB+15(−−→BA+−−→AD)
=45−−→AB+15−−→AD
又 −−→AC=−−→AB+−−→AD,
则 −−→AE⋅−−→AC=(45−−→AB+15−−→AD)(−−→AB+−−→AD)=45−−→AB2+15−−→AD2
=45×4+45×4=325, 故选 C .
在 △ABC 中 AB=3,AC=2,∠BAC=120∘,点 D 为 BC 边上的一点 且 −−→BD=2−−→DC, 则 −−→AB⋅−−→AD 等于【】
A.23 B.1 C.2 D.13
解析: 以 A 为坐标原点 AB 所在的直线为 x 轴建立平面直角坐标系如图所示.

则 A(0,0), B(3,0), C(−1,√3),
由于 −−→BD=2−−→DC, 所以 −−→BD=23−−→BC=23(−4,√3)=(−83,2√33),
则 D(13,2√33), 则 −−→AD=(13,2√33),−−→AB=(3,0)
所以, −−→AB⋅−−→AD=3×13+0×2√33=1, 故选 B .
中阶提升
- 平面问题中若涉及轨迹问题,常可以建立平面直角坐标系;
在边长为 2 的正 △ABC 中,若 P 为 △ABC 内一点,且 |PA|2=|PB|2+|PC|2,求点 P 的轨迹方程,并画出方程所表示的曲线。
分析:本题目是曲线方程的确定与应用问题,考查建立平面直角坐标系、数形结合思想、曲线方程的求法及分析推理、计算化间技能、技巧等。解答需要先建立平面直角坐标系,写出各点的坐标,用直接法求解,再根据方程判定曲线类型画出其表示的曲线。
解析:以 BC 所在直线为 x 轴,BC 的中点为原点,BC 的中垂线为 y 轴建立平面直角坐标系,
设 P(x,y) 是轨迹上任意一点,又 |BC|=2, 故有 B(−1,0), C(1,0), 则 A(0,√3),
由于 |PA|2=|PB|2+|PC|2,
即 x2+(y−√3)2=(x+1)2+y2+(x−1)2+y2,
化简得到, x2+(y+√3)2=4,
又由于点 P 在 △ABC 内, 所以 y>0,
所以, P 点的轨迹方程为 x2+(y+√3)2=4(y>0).
其轨迹如图所示,为以 (0,−√3) 为圆心,半径为 2 的圆在 x 轴上方的圆弧.
对应练习
【2025 届学生问题】已知梯形 ABCD 中,AD//BC ,∠B=π3,AB=2,BC=4,AD=1,点 P 和点 Q 在线段 BC 上移动且 PQ=1,则 −−→DP⋅−−→DQ 的最小值为_______________ .
解:注意到梯形是相对比较特殊的图形,故可以考虑建立平面直角坐标系,利用坐标来计算;分别过点 A 和点 D 做 BC 的垂线,垂足分别为 E 和 F,以点 E 为坐标原点,以 EC 和 EA 所在的直线为 x 和 y 轴,建立如图所示的直角坐标系,
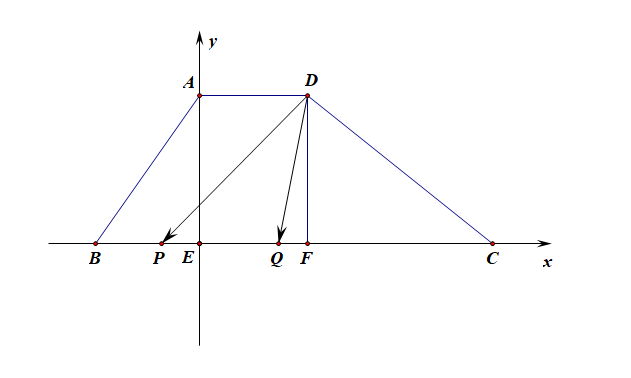
由 ∠B=π3,AB=2,BC=4,AD=1,则可知 D(1,√3),不妨令动点 P 在 Q 的左侧,设点 P(x,0),则 Q(x+1,0),则 x∈[−1,2],这样,−−→DP=(x−1,−√3),−−→DQ=(x,−√3),
则 −−→DP⋅−−→DQ=(x−1)x+3=x2−x+3, x∈[−1,2],
利用二次函数可得,y=f(x)=x2−x+3=(x−12)2+114,x∈[−1,2],
故 f(x)min=f(12)=14,故 −−→DP⋅−−→DQ 的最小值为 14 .
高阶延申


 在平面图形中若涉及相关的计算,可以考虑建立平面直角坐标系来计算
在平面图形中若涉及相关的计算,可以考虑建立平面直角坐标系来计算









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架