正三棱台

前情概要

正三棱台的概念，表面积，体积公式，相比较棱柱和棱锥，我们对棱台不是非常熟悉，尤其是其体积公式，请参阅相关内容 .

动态演示

结合上图，你能说出正三棱台的各部分的名称吗？请注意区分正三棱台的高 和 斜高 .

正三棱台画法

形是数的依托，所以，要掌握快速画正三棱台的方法，由上述的动态课件，你能找到比较理想的绘制角度吗？以下仅为参考 .

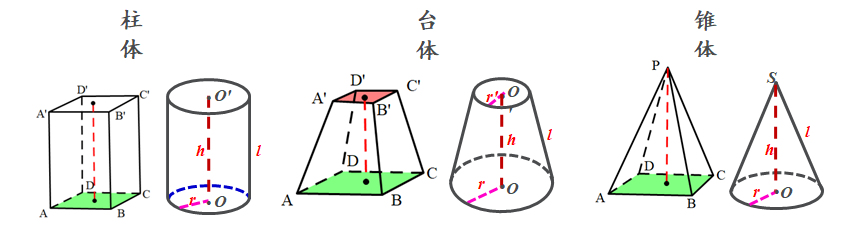
体积公式及记忆方法

• 棱柱棱锥棱台的体积转化： 教材上推导出多面体的体积，然后依托祖暅原理得到旋转体的体积。

$ V_{棱柱}=S\times h$ $\xleftarrow[代入整理]{令S'=S}$ $V_{棱台}=\cfrac{1}{3}\times (S'+\sqrt{S'S}+S)\times h$ $\xrightarrow[代入整理]{令S'=0}$ $V_{棱锥}=\cfrac{1}{3}\times S\times h$

\[\downarrow \]

$ V_{圆柱}=S\times h$ $\xleftarrow[代入整理]{令S'=S}$ $V_{圆台}=\cfrac{1}{3}\times (S'+\sqrt{S'S}+S)\times h$ $\xrightarrow[代入整理]{令S'=0}$ $V_{圆锥}=\cfrac{1}{3}\times S\times h$

\[\downarrow \]

$ V_{柱体}=S\times h$ $\xleftarrow[代入整理]{令S'=S}$ $V_{台体}=\cfrac{1}{3}\times (S'+\sqrt{S'S}+S)\times h$ $\xrightarrow[代入整理]{令S'=0}$ $V_{锥体}=\cfrac{1}{3}\times S\times h$

典例剖析

【2025届高三质检一试题】已知正三棱台 \(ABC-A_1B_1C_1\) 的上底面积为 \(\sqrt{3}\)，下底面积为 \(4\sqrt{3}\)，高为 \(2\)，则该三棱台的表面积为 【\(\qquad\)】

$A.5\sqrt{3}+3\sqrt{39}$ $B.3\sqrt{39}$ $C.5\sqrt{3}+18$ $D.18$

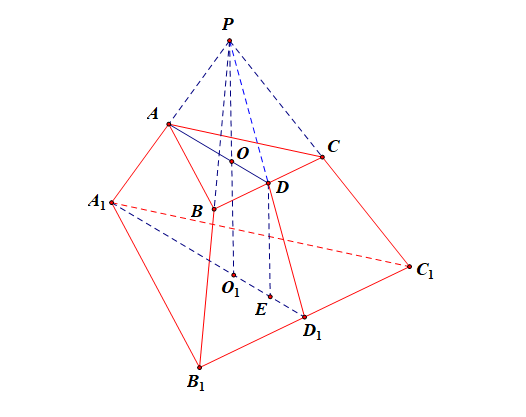
解：正三棱台的上下底面为正三角形，由正三角形的面积公式 \(S_{正\triangle}=\cfrac{\sqrt{3}}{4}a^2\)，^[1] 其中 \(a\) 为正三角形的边长，则由 \(\cfrac{\sqrt{3}}{4}a^2=\sqrt{3}\) 或 \(\cfrac{\sqrt{3}}{4}a^2=4\sqrt{3}\) ，可得上下底的边长分别为 \(2\) 和 \(4\)，即 \(BC=2\)，\(B_1C_1=4\)，设上下底面的中心分别为点 \(O\) 和 \(O_1\)，则 \(AD\) 和 \(A_1D_1\) 分别是上下底三角形的高线，连结 \(DD_1\)，则 \(DD_1\) 是正三棱台的斜高，过点 \(D\) 作 \(DE\perp A_1D_1\) 于点 \(E\)，则 \(D_1E\) 是斜高 \(DD_1\) 的投影；

由三角形的知识可知，\(OD=\cfrac{1}{3}AD\)\(=\)\(\cfrac{\sqrt{3}}{3}\)，\(O_1D_1\)\(=\)\(\cfrac{1}{3}A_1D_1\)\(=\)\(\cfrac{1}{3}\times2\sqrt{3}\)\(=\)\(\cfrac{2\sqrt{3}}{3}\)，则 \(D_1E=\cfrac{\sqrt{3}}{3}\)，

在 \(Rt\triangle DD_1E\) 中，由勾股定理可知 \(DD_1=\cfrac{\sqrt{39}}{3}\)，

又正三棱台的侧面为等腰梯形， \(S_{BCC_1B_1}=\cfrac{(2+4)\times\frac{\sqrt{39}}{3}}{2}=\sqrt{39}\)，

故该三棱台的表面积为 \(S=\sqrt{3}+4\sqrt{3}+3\times\sqrt{39}=5\sqrt{3}+3\sqrt{39}\)，故选 \(A\) .

【2024新课标全国Ⅱ卷数学第7题】已知正三棱台 \(ABC-A_1B_1C_1\) 的体积为 \(\cfrac{52}{3}\)，\(AB=6\)，\(A_1B_1=2\)，则 \(A_1A\) 与平面 \(ABC\) 所成角的正切值为 【\(\qquad\)】

$A.\cfrac{1}{2}$ $B.1$ $C.2$ $D.3$

法一：由正三角形的面积公式 \(S_{正\triangle}\)\(=\)\(\cfrac{\sqrt{3}}{4}a^2\)，

可得 \(S_{\triangle ABC}\)\(=\)\(\cfrac{\sqrt{3}}{4}\)\(\times\)$ 6^2$$=$$9\sqrt{3}$， \(S_{\triangle A_1B_1C_1}\)\(=\)\(\cfrac{\sqrt{3}}{4}\)\(\times\)\(2^2\)\(=\)\(\sqrt{3}\)，

如图，设正三棱台 \(ABC-A_1B_1C_1\) 的高为 \(h\)，则由 \(V_{正三棱台}\)\(=\)\(\cfrac{1}{3}\times(S'+\sqrt{S'S}+S)\times h\)

\(=\)\(\cfrac{1}{3}(9\sqrt{3}+\sqrt{3}+\sqrt{9\sqrt{3}\times\sqrt{3}})h\)\(=\)\(\cfrac{52}{3}\)，解得 \(h=\cfrac{4\sqrt{3}}{3}\)，

由图分别取 \(BC\)，\(B_1C_1\) 的中点 \(D\)、\(D_1\)，分别过 \(A_1\)、\(D_1\) 作底面垂线，垂足为 \(M\)、\(N\)，则 \(A_1D_1=\sqrt{3}=MN\)，\(AD=3\sqrt{3}\)，

设 \(AM=x\)，则 \(AA_1=\sqrt{x^2+(\cfrac{4\sqrt{3}}{3})^2}\)\(=\)\(BB_1\)\(=\)\(CC_1\)，\(ND\)\(=\)\(2\sqrt{3}-x\)，

则 \(DD_1\)\(=\)\(\sqrt{(2\sqrt{3}-x)^2+(\cfrac{4\sqrt{3}}{3})^2}\)，

结合直角梯形 \(BDD_1B_1\) 可得，\(BB_1^2=DD_1^2+(\cfrac{6-2}{2})^2\) 上述的 \(BB_1^2\) 和 \(DD_1^2\) 不要急着展开合并整理，在这个式子中会相互抵消，这样运算能快一些。，解得 \(x=\cfrac{4\sqrt{3}}{3}\)，

故 \(A_1A\) 与平面 \(ABC\) 所成角的正切值为 \(\tan\angle A_1AD=\cfrac{A_1M}{AM}=\cfrac{h}{x}=1\)，故选 \(B\) .

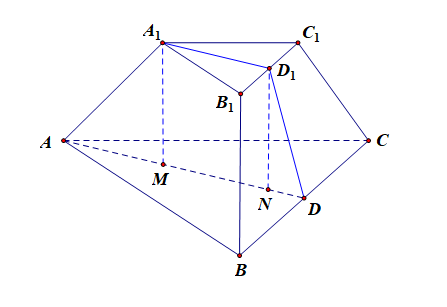
法2：补体法，将正三棱台 \(ABC-A_1B_1C_1\) 补体成正三棱锥 \(P-ABC\)，则 \(A_1A\) 与平面 \(ABC\) 所成角即为 \(PA\) 与平面 \(ABC\) 所成角，如下图所示，

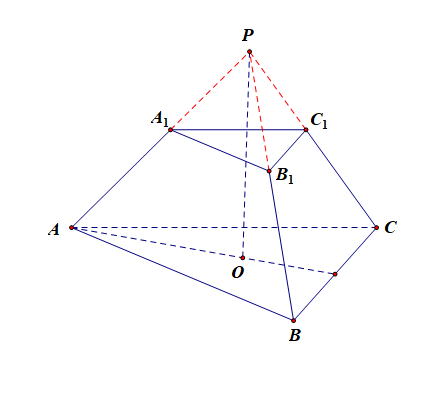
由于 \(\cfrac{PA_1}{PA}=\cfrac{A_1B_1}{AB}=\cfrac{1}{3}\)，则\(\cfrac{V_{P-A_1B_1C_1}}{V_{P-ABC}}=\cfrac{1}{27}\)在立体图形中，相似体[平面图形中成为相似形]的一切对应线段（或弧）长的比等于相似比。相似体的表面积的比等于相似比的平方。相似体的体积的比等于相似比的立方。我们甚至可以自行证明这个结论。，

可知 \(V_{A_1B_1C_1-ABC}=\cfrac{26}{27} V_{P-ABC}=\cfrac{52}{3}\)，则 \(V_{P-ABC}=18\) ，

设正三棱锥 \(P-ABC\) 的高为 \(h\)，则 \(V_{P-ABC}=\cfrac{1}{3}Sh=\cfrac{1}{3}(\cfrac{1}{2}\times 6\times 6\times\cfrac{\sqrt{3}}{2})h=18\)，

解得 \(h=2\sqrt{3}\)，取底面 \(ABC\) 的中心为 \(O\)，则 \(PO=h=2\sqrt{3}\)，\(PO\perp\) 底面 \(ABC\)，

且由勾股定理可知 \(AO=\cfrac{2}{3}(3\sqrt{3})=2\sqrt{3}\)，

所以 \(PA\) 与平面 \(ABC\) 所成角的正切值 \(\tan\angle PAO=\cfrac{PO}{AO}=1\)，故选：\(B\) .

---

1. 更多的有关三角形的面积计算方法，请参阅 三角形的面积公式 ↩︎