前言
相关内容
在初中数学中我们已经知道,当 a a b b a b = 1 4 [ ( a + b ) 2 − ( a − b ) 2 ] a b = 1 4 [ ( a + b ) 2 − ( a − b ) 2 ] a a b b → a a → → b b →
→ a ⋅ → b = 1 4 [ ( → a + → b ) 2 − ( → a − → b ) 2 ] a → ⋅ b → = 1 4 [ ( a → + b → ) 2 − ( a → − b → ) 2 ]
证明:由向量的知识我们知道,
( → a + → b ) 2 = → a 2 + 2 → a ⋅ → b + → b 2 ( a → + b → ) 2 = a → 2 + 2 a → ⋅ b → + b → 2 ① ①
( → a − → b ) 2 = → a 2 − 2 → a ⋅ → b + → b 2 ( a → − b → ) 2 = a → 2 − 2 a → ⋅ b → + b → 2 ② ②
①-② 整理得到,→ a ⋅ → b = 1 4 [ ( → a + → b ) 2 − ( → a − → b ) 2 ] a → ⋅ b → = 1 4 [ ( a → + b → ) 2 − ( a → − b → ) 2 ]
相关形的计算
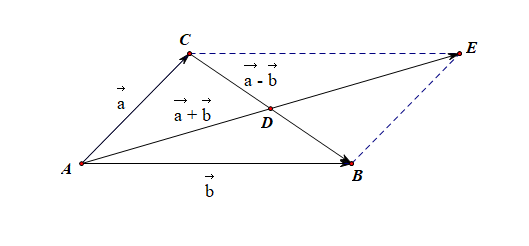
将极化恒等式 → a ⋅ → b = 1 4 [ ( → a + → b ) 2 − ( → a − → b ) 2 ] a → ⋅ b → = 1 4 [ ( a → + b → ) 2 − ( a → − b → ) 2 ] − − → A B ⋅ − − → A C = 1 4 ( − − → A E 2 − − − → C B 2 ) A B → ⋅ A C → = 1 4 ( A E → 2 − C B → 2 )
也能得到 − − → A B ⋅ − − → A C = − − → A D 2 − − − → D B 2 A B → ⋅ A C → = A D → 2 − D B → 2
典例剖析
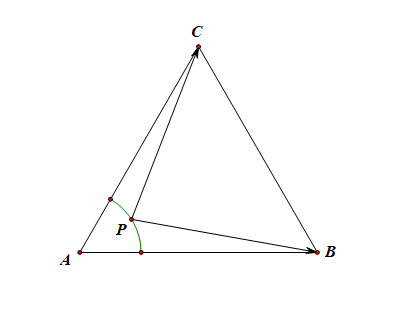
4 4 A B C A B C P P △ A B C △ A B C P A = 1 P A = 1
(1). 求 | − − → A C + − − → A B | | A C → + A B → |
提示:以退为进策略,先平方再开方,具体过程略,4 √ 3 4 3
(2). 求 − − → P B ⋅ − − → P C P B → ⋅ P C →
法一:三角函数法,
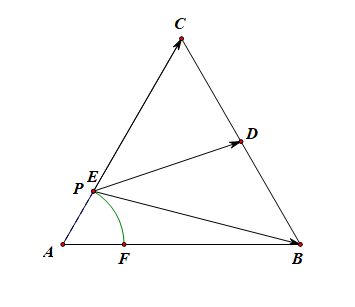
法二:极化恒等式法,取 B C B C D D P D P D D B = 2 D B = 2
则 − − → P B ⋅ − − → P C = ( − − → P D + − − → D B ) ⋅ ( − − → P D + − − → D C ) = ( − − → P D + − − → D B ) ⋅ ( − − → P D − − − → D B ) P B → ⋅ P C → = ( P D → + D B → ) ⋅ ( P D → + D C → ) = ( P D → + D B → ) ⋅ ( P D → − D B → )
= | − − → P D | 2 − | − − → D B | 2 = | − − → P D | 2 − 4 = | P D → | 2 − | D B → | 2 = | P D → | 2 − 4
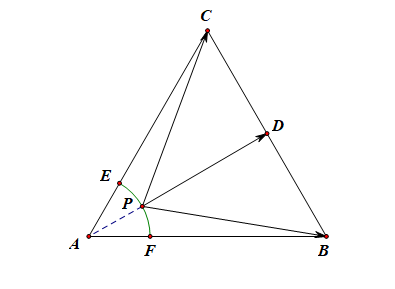
由图可知,当点 P P | − − → P D | | P D → | | − − → P D | m i n = 2 √ 3 − 1 | P D → | m i n = 2 3 − 1
此时,− − → P B ⋅ − − → P C m i n = | − − → P D | 2 m i n − 4 = ( 2 √ 3 − 1 ) 2 − 4 = 9 − 4 √ 3 P B → ⋅ P C → m i n = | P D → | m i n 2 − 4 = ( 2 3 − 1 ) 2 − 4 = 9 − 4 3
当点 P P E E F F | − − → P D | | P D → | | − − → P D | m a x = √ 7 | P D → | m a x = 7
此时,− − → P B ⋅ − − → P C m a x = | − − → P D | 2 m a x − 4 = ( √ 7 ) 2 − 4 = 3 P B → ⋅ P C → m a x = | P D → | m a x 2 − 4 = ( 7 ) 2 − 4 = 3
故 − − → P B ⋅ − − → P C P B → ⋅ P C → [ 9 − 4 √ 3 , 3 ] [ 9 − 4 3 , 3 ]
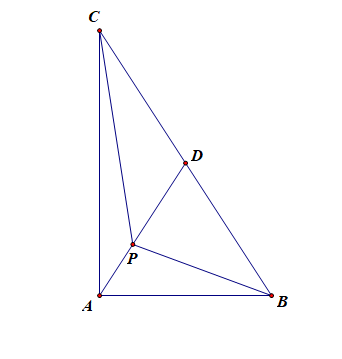
R t △ A B C R t △ A B C ∠ A = 90 ∘ ∠ A = 90 ∘ A B = 2 A B = 2 A C = 6 A C = 6 D D B C B C P P △ A B C △ A B C 斜边 B C B C A D A D − − → P B ⋅ − − → P C P B → ⋅ P C → 【
A . [ − 10 , 0 ] A . [ − 10 , 0 ] B . [ − 6 , 0 ] B . [ − 6 , 0 ] C . [ 0 , 6 ] C . [ 0 , 6 ] D . [ 0 , 10 ] D . [ 0 , 10 ]
解法 1️⃣:特殊化策略法;由于点 P P B C B C A D A D P P A A − − → P C P C → − − → P B P B → − − → P B ⋅ − − → P C = 0 P B → ⋅ P C → = 0 P P D D − − → P C P C → − − → P B P B → π π D D 为 B C B C C D = B D = √ 10 C D = B D = 10 ,故 − − → P B ⋅ − − → P C = − 10 P B → ⋅ P C → = − 10 − − → P B ⋅ − − → P C P B → ⋅ P C → [ − 10 , 0 ] [ − 10 , 0 ] ,故 选 A A
解法 2️⃣:极化恒等式法; 由题可知,则 D B = D C = √ 10 D B = D C = 10
则 − − → P B ⋅ − − → P C = ( − − → P D + − − → D B ) ⋅ ( − − → P D + − − → D C ) = ( − − → P D + − − → D B ) ⋅ ( − − → P D − − − → D B ) P B → ⋅ P C → = ( P D → + D B → ) ⋅ ( P D → + D C → ) = ( P D → + D B → ) ⋅ ( P D → − D B → )
= | − − → P D | 2 − | − − → D B | 2 = | − − → P D | 2 − 10 = | P D → | 2 − | D B → | 2 = | P D → | 2 − 10
由图可知,当点 P P A A | − − → P D | | P D → | | − − → P D | m a x = 0 | P D → | m a x = 0
由图可知,当点 P P D D | − − → P D | | P D → | | − − → P D | m i n = − 10 | P D → | m i n = − 10
即 − − → P B ⋅ − − → P C P B → ⋅ P C → [ − 10 , 0 ] [ − 10 , 0 ] ,故 选 A A
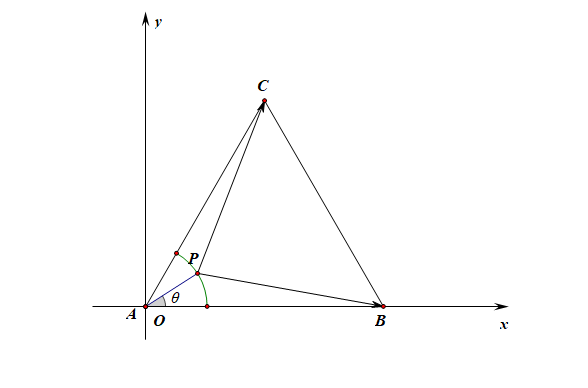
解法 3️⃣:二次函数法;由于 点 D B = D C = D A D B = D C = D A D ( 1 , 3 ) D ( 1 , 3 ) P ( x , y ) P ( x , y ) x y = 1 3 x y = 1 3 y = 3 x y = 3 x
则有 P ( x , 3 x ) P ( x , 3 x ) B ( 2 , 0 ) B ( 2 , 0 ) C ( 0 , 6 ) C ( 0 , 6 )
故 − − → P B = ( 2 − x , − 3 x ) P B → = ( 2 − x , − 3 x ) − − → P C = ( − x , 6 − 3 x ) P C → = ( − x , 6 − 3 x )
则 − − → P B ⋅ − − → P C = ( 2 − x ) ( − x ) + ( − 3 x ) ( 6 − 3 x ) = 10 x 2 − 20 x = 10 ( x − 1 ) 2 − 10 P B → ⋅ P C → = ( 2 − x ) ( − x ) + ( − 3 x ) ( 6 − 3 x ) = 10 x 2 − 20 x = 10 ( x − 1 ) 2 − 10 x ∈ [ 0 , 1 ] x ∈ [ 0 , 1 ]
故 x = 0 x = 0 − − → P B ⋅ − − → P C m a x = 0 P B → ⋅ P C → m a x = 0
x = 1 x = 1 − − → P B ⋅ − − → P C m i n = − 10 P B → ⋅ P C → m i n = − 10
即 − − → P B ⋅ − − → P C P B → ⋅ P C → [ − 10 , 0 ] [ − 10 , 0 ] ,故 选 A A
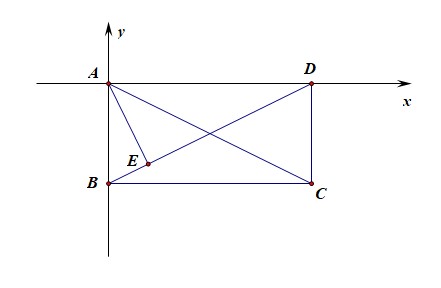
A B C D A B C D 中,A B = 2 A B = 2 A D = 4 A D = 4 A C A C B D B D 相交于点 O O ,过点 A A 作 A E ⊥ B D A E ⊥ B D 于 E E ,则 − − → A E ⋅ − − → A C A E → ⋅ A C → =【
A . 8 5 A . 8 5 B . 16 5 B . 16 5 C . 32 5 C . 32 5 D .8 D .8
解法 1️⃣ :从形的角度思考,采用坐标法求解;以点 A A 为坐标原点建立如图所示的直角坐标系,
则可知 A ( 0 , 0 ) A ( 0 , 0 ) B ( 0 , − 2 ) B ( 0 , − 2 ) C ( 4 , − 2 ) C ( 4 , − 2 ) D ( 4 , 0 ) D ( 4 , 0 ) E ( x , y ) E ( x , y )
则由 k A E k A E ⋅ ⋅ k B D k B D = = − 1 − 1 y y = = − 2 x − 2 x B D B D :2 y 2 y = = x − 4 x − 4
联立①②可得,x x = = 4 5 4 5 y y = = − 8 5 − 8 5
则 − − → A E A E → ⋅ ⋅ − − → A C A C → = = ( 4 5 , − 8 5 ) ( 4 5 , − 8 5 ) ⋅ ⋅ ( 4 , − 2 ) ( 4 , − 2 ) = = 32 5 32 5 C C
解法 2️⃣ :本题目还可以用基向量法,以 − − → A B A B → 和 − − → A D A D → 为基向量来表示其他向量,
由射影定理 可知,A B 2 A B 2 = = B E B E ⋅ ⋅ B D B D B D B D = = 2 2 √ 5 5 B E B E = = 2 √ 5 5 2 5 5
令 − − → B E B E → = = t t − − → B D B D → t t = = | − − → B E | | − − → B D | | B E → | | B D → | = = 1 5 1 5
又 − − → A E A E → = = − − → A B A B → + + − − → B E B E → = = − − → A B A B → + + 1 5 1 5 − − → B D B D →
= = − − → A B A B → + + 1 5 1 5 ( − − → B A ( B A → + + − − → A D ) A D → )
= = 4 5 4 5 − − → A B A B → + + 1 5 1 5 − − → A D A D →
又 − − → A C A C → = = − − → A B A B → + + − − → A D A D →
则 − − → A E A E → ⋅ ⋅ − − → A C A C → = = ( 4 5 − − → A B ( 4 5 A B → + + 1 5 − − → A D 1 5 A D → − − → A B A B → + + − − → A D A D → = = 4 5 − − → A B 2 4 5 A B → 2 + + 1 5 − − → A D 2 1 5 A D → 2
= 4 5 = 4 5 × × 4 4 + + 4 5 4 5 × × 4 4 = = 32 5 32 5 C C
思考:此题目能使用极化恒等式吗?下题呢,待有空思考
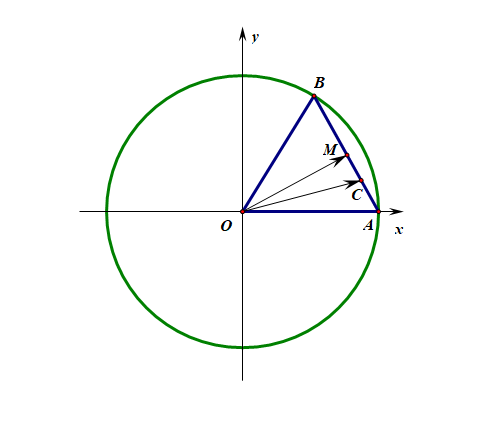
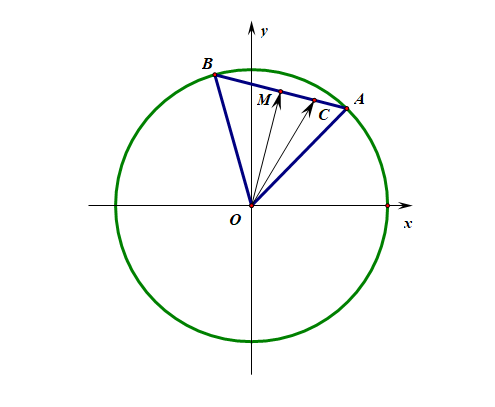
A A B B O : x 2 + y 2 = 4 O : x 2 + y 2 = 4 | − − → A B | = 2 | A B → | = 2 − − → O C = 1 3 − − → O A + 2 3 − − → O B O C → = 1 3 O A → + 2 3 O B → M M A B A B − − → O C ⋅ − − → O M O C → ⋅ O M → 【
A . √ 3 A . 3 B .2 √ 3 B .2 3 C .2 C .2 D .3 D .3
法 1:基向量法,即以向量 − − → O A O A → − − → O B O B → − − → O C O C → − − → O M O M →
因为 − − → O C = 1 3 − − → O A + 2 3 − − → O B O C → = 1 3 O A → + 2 3 O B → − − → O M = 1 2 ( − − → O A + − − → O B ) O M → = 1 2 ( O A → + O B → )
所以 − − → O C ⋅ − − → O M = ( 1 3 − − → O A + 2 3 − − → O B ) ⋅ 1 2 ( − − → O A + − − → O B ) O C → ⋅ O M → = ( 1 3 O A → + 2 3 O B → ) ⋅ 1 2 ( O A → + O B → )
= 1 6 ( − − → O A 2 + 2 − − → O B 2 + 3 − − → O A ⋅ − − → O B ) = 1 6 ( O A → 2 + 2 O B → 2 + 3 O A → ⋅ O B → )
又 △ O A B △ O A B − − → O A ⋅ − − → O B = 2 × 2 cos 60 ∘ = 2 O A → ⋅ O B → = 2 × 2 cos 60 ∘ = 2 − − → O A 2 = 4 O A → 2 = 4 − − → O B 2 = 4 O B → 2 = 4
所以 − − → O C ⋅ − − → O M = 3 O C → ⋅ O M → = 3 D D
法 2:特殊化策略,【考试中的首选方法】既然点 A A B B 为什么可以这样思考呢,由于点 C C M M A B A B A A B B | − − → O C | | O C → | | − − → O M | | O M → | − − → O C ⋅ − − → O M O C → ⋅ O M → A A ,那么可以将点 A A ( 2 , 0 ) ( 2 , 0 ) | A B | = 2 | A B | = 2 △ O A B △ O A B B B ( 1 , √ 3 ) ( 1 , 3 ) − − → O A = ( 2 , 0 ) O A → = ( 2 , 0 ) − − → O B = ( 1 , √ 3 ) O B → = ( 1 , 3 )
则 − − → O C O C → = = 1 3 − − → O A 1 3 O A → + + 2 3 − − → O B 2 3 O B → = = 1 3 ( 2 , 0 ) 1 3 ( 2 , 0 ) + + 2 3 ( 1 , √ 3 ) 2 3 ( 1 , 3 ) = = ( 4 3 , 2 √ 3 3 ) ( 4 3 , 2 3 3 )
又由于点 M M A B A B M ( 3 2 , √ 3 2 ) M ( 3 2 , 3 2 ) − − → O M O M → = = ( 3 2 , √ 3 2 ) ( 3 2 , 3 2 )
故 − − → O C ⋅ − − → O M | = ( 4 3 , 2 √ 3 3 ) ⋅ ( 3 2 , √ 3 2 ) = 3 O C → ⋅ O M → | = ( 4 3 , 2 3 3 ) ⋅ ( 3 2 , 3 2 ) = 3 D D
法 3:向量坐标法,如果上述的方法理解还是有疑虑,那么可以采用这个方法来计算打消我们的顾虑,就是运算比较麻烦。
由于点 A A B B | A B | = 2 | A B | = 2 r = 2 r = 2 △ O A B △ O A B A ( 2 cos θ , 2 sin θ ) A ( 2 cos θ , 2 sin θ ) B ( 2 cos ( θ + π 3 ) , 2 sin ( θ + π 3 ) ) B ( 2 cos ( θ + π 3 ) , 2 sin ( θ + π 3 ) )
− − → O A O A → = = ( 2 cos θ , 2 sin θ ) ( 2 cos θ , 2 sin θ ) − − → O B O B → = = ( 2 cos ( θ + π 3 ) , 2 sin ( θ + π 3 ) ) ( 2 cos ( θ + π 3 ) , 2 sin ( θ + π 3 ) )
− − → O C O C → = = 1 3 − − → O A 1 3 O A → + + 2 3 − − → O B 2 3 O B → = = ( 2 3 cos θ + 4 3 cos ( θ + π 3 ) , 2 3 sin θ + 4 3 sin ( θ + π 3 ) ) ( 2 3 cos θ + 4 3 cos ( θ + π 3 ) , 2 3 sin θ + 4 3 sin ( θ + π 3 ) )
− − → O M O M → = = ( cos θ + cos ( θ + π 3 ) , sin θ + sin ( θ + π 3 ) ) ( cos θ + cos ( θ + π 3 ) , sin θ + sin ( θ + π 3 ) )
故 − − → O C ⋅ − − → O M O C → ⋅ O M → = = [ 2 3 cos θ + 4 3 cos ( θ + π 3 ) ] [ 2 3 cos θ + 4 3 cos ( θ + π 3 ) ] [ cos θ + cos ( θ + π 3 ) ] [ cos θ + cos ( θ + π 3 ) ]
+ + [ 2 3 sin θ + 4 3 sin ( θ + π 3 ) ] [ 2 3 sin θ + 4 3 sin ( θ + π 3 ) ] [ sin θ + sin ( θ + π 3 ) ] [ sin θ + sin ( θ + π 3 ) ]
= = 2 3 cos 2 θ 2 3 cos 2 θ + + 2 3 sin 2 θ 2 3 sin 2 θ + + 4 3 cos 2 ( θ + π 3 ) 4 3 cos 2 ( θ + π 3 ) + + 4 3 sin 2 ( θ + π 3 ) 4 3 sin 2 ( θ + π 3 )
+ + 2 3 [ cos θ cos ( θ + π 3 ) + sin θ sin ( θ + π 3 ) ] 2 3 [ cos θ cos ( θ + π 3 ) + sin θ sin ( θ + π 3 ) ] + + 4 3 [ cos θ cos ( θ + π 3 ) + sin θ sin ( θ + π 3 ) ] 4 3 [ cos θ cos ( θ + π 3 ) + sin θ sin ( θ + π 3 ) ]
= 2 + 2 cos ( θ − θ − π 3 ) = 2 + 1 = 3 = 2 + 2 cos ( θ − θ − π 3 ) = 2 + 1 = 3 D D

 极化恒等式相关
极化恒等式相关



【推荐】国内首个 AI IDE,深度理解中文开发场景,立即下载体验 Trae
【推荐】编程新体验,更懂你的 AI,立即体验豆包 MarsCode 编程助手
【推荐】抖音旗下 AI 助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 如何调用 DeepSeek 的自然语言处理 API 接口并集成到在线客服系统
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App