球体与棱柱的切接问题

前言

球体与正三棱柱

• 正三棱柱不一定有内切球和棱切球，但一定有外接球。正三棱柱的外接球的球心是上下底面中心连线的中点，

关键关系：正三棱柱的高为 \(h\)，正三棱柱的底面外接圆的半径 \(r\) 与球的半径 \(R\) 之间的关系为 \((\cfrac{h}{2})^2+r^2=R^2\) .

球体与直棱柱

• 直三棱柱的外接球的球心是上下底面三角形外心连线的中点。如下图直三棱柱的外接球的球心 \(O\) 应该是上下底面三角形外心 \(O'\) 与 \(O''\) 连线的中点 .

关键关系：直三棱柱的高为 \(h\)，直三棱柱的底面外接圆的半径 \(r\) 与球的半径 \(R\) 之间的关系为 \((\cfrac{h}{2})^2+r^2=R^2\) .

典型例题

【2024级高一数学训练题】已知体积为 \(\cfrac{4\pi}{3}\) 的球 \(O_1\) 与正三棱柱 \(ABC-A_1B_1C_1\) 的所有面都相切，则三棱柱 \(ABC-A_1B_1C_1\) 外接球的表面积为 【\(\qquad\)】

$A.24\pi$ $B.20\pi$ $C.16\pi$ $D.12\pi$

解：由题可知，正三棱柱的内切球的半径为 \(1\)，如图可知，正三棱柱的高等于球的直径，故正三棱柱的高为 \(h=2\)，点 \(O\) 既是正三棱柱的内切球的球心，也是正三棱柱的外接球的球心，点 \(M\) 是正三棱柱的下底面的外接圆的圆心，故 \(r\)\(=\)\(BM\)\(=\)\(2\)，

则由 \((\cfrac{h}{2})^2+r^2=R^2\) 可知，正三棱柱的外接球的半径 \(R=\sqrt{5}\)，故外接球的表面积为 \(4\pi R^2=20\pi\)，故选 \(B\) .

【2025届高三数学月考二用题】已知三棱锥 \(A-BCD\) 的所有顶点都在球 \(O\) 的球面上，\(AD\perp\) 平面 \(ABC\)，\(\angle BAC=\cfrac{\pi}{2}\)，\(AD=2\)，若球 \(O\) 的表面积为 \(22\pi\)，则三棱锥 \(A-BCD\) (以 \(A\) 为顶点）的侧面积的最大值为【\(\qquad\)】

$A.6$ $B.\cfrac{21}{2}$ $C.\cfrac{25}{2}$ $D.\cfrac{27}{2}$

解析：由于 \(AD\)、\(AB\)、\(AC\) 两两垂直，故考虑将其补体为直三棱柱 \(DEF-ABC\)，\(O_1\)、\(O_2\) 分别是上下底面三角形的外接圆的圆心，则 \(O_1O_2\) 的中点 \(O\) 为此直三棱柱[也是原三棱锥]的外接球的球心，

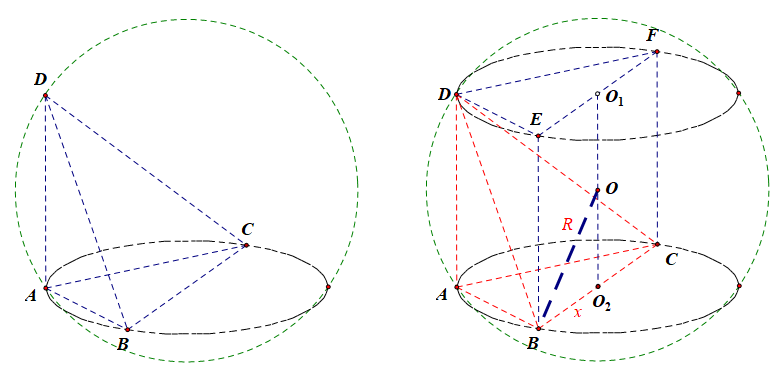
由球 \(O\) 的表面积为 \(22\pi\)，则 \(4\pi R^2=22\pi\)，解得 \(R^2=\cfrac{11}{2}\)，由于 \(AD=2=O_1O_2\)，故 \(OO_2=1\)，令 \(BO_2=x\)，则 \(1^2+x^2=R^2\)，故 \(x^2=\cfrac{9}{2}\)，则 \(BC=2x=3\sqrt{2}\)，

再令 \(AB=m\)，\(AC=n\)，则三棱锥 \(A-BCD\) (以 \(A\) 为顶点）的侧面积 \(S_{侧}\)\(=\)\(\cfrac{1}{2}mn\)\(+\)\(m\)\(+\)\(n\)，且有 \(m,n>0\)，\(m+n\)\(>\)\(3\sqrt{2}\)(两边之和大于第三边)，\(m^2\)\(+\)\(n^2\)\(=\)\(18\)(勾股定理)，接下来求解 \(S_{侧}\)\(=\)\(f(m,n)\)\(=\)\(\cfrac{1}{2}mn\)\(+\)\(m\)\(+\)\(n\) 的最大值， \(f(m,n)_{\max}\)\(=\)\(\cfrac{21}{2}\) ，故选 \(B\) . 详细求解过程