球体与正六面体[正方体]切接
前言
当两个非常特殊的多面体 [正六面体] 和旋转体 [球] 邂逅,会发生许多有趣的故事。
常用结论
-
给定一个棱长为 \(a\) 的正方体[即正六面体],则其面对角线长为\(\sqrt{2}a\),其体对角线长为\(\sqrt{3}a\);且正六面体棱长、面对角线、体对角线三者之比为\(1\)\(\;:\;\)\(\sqrt{2}\)\(\;:\;\)\(\sqrt{3}\);
-
设正方体的棱长为 \(a\),则内切球的半径\(R_{内}=\cfrac{a}{2}\);棱切球的半径\(R_{棱}=\cfrac{\sqrt{2}a}{2}\);外接球的半径\(R_{外}=\cfrac{\sqrt{3}a}{2}\);且内切球半径 \(R_{内}\)、棱切球半径\(R_{棱}\)、外接球半径\(R_{外}\) 三者之比为 \(1\)\(\;:\;\)\(\sqrt{2}\)\(\;:\;\)\(\sqrt{3}\);
-
相关计算和说明:正方体棱长为 \(a\),点 \(O\) 为正六面体的中心,则内切球的半径\(R_{内}\)\(=\)\(OF\)\(=\)\(\cfrac{a}{2}\);棱切球的半径\(R_{棱}\)\(=\)\(OG\)\(=\)\(\cfrac{\sqrt{2}a}{2}\);外接球的半径\(R_{外}\)\(=\)\(OC\)\(=\)\(\cfrac{\sqrt{3}a}{2}\);
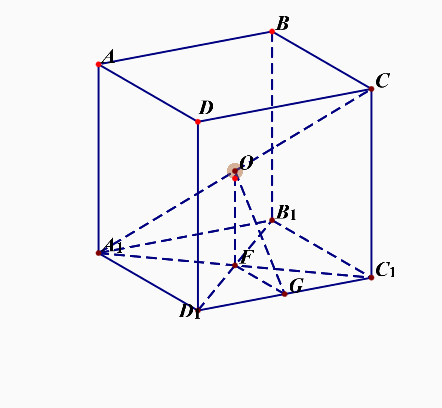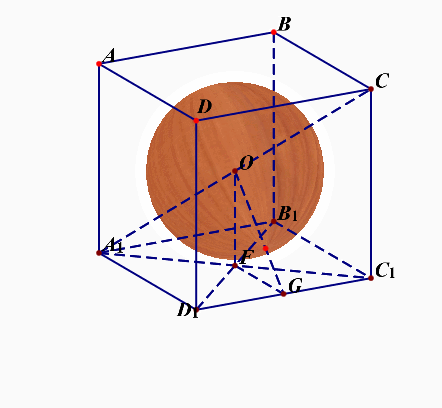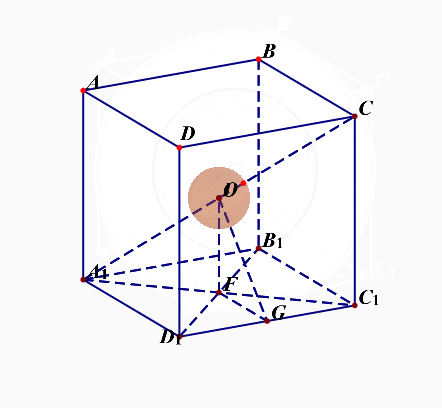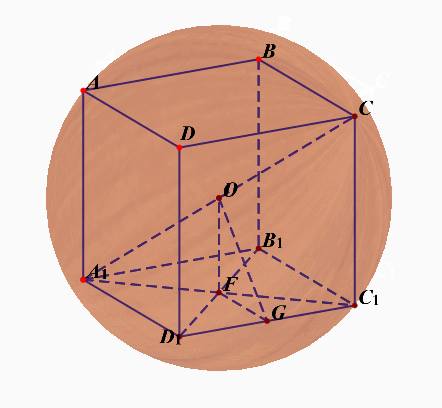
- 正方体的内切球球心、棱切球球心、外接球球心都是体对角线的中点,也即正六面体的中心。
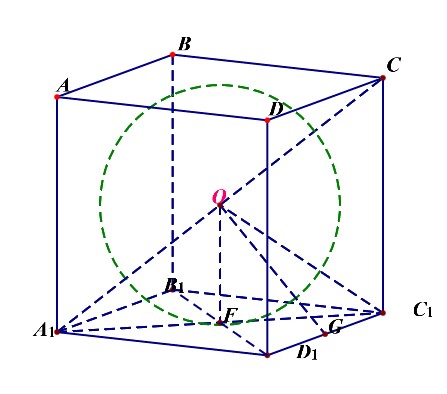

正方体与各条棱相切的球的半径\(R_{棱}=\cfrac{\sqrt{2}a}{2}=OG\);
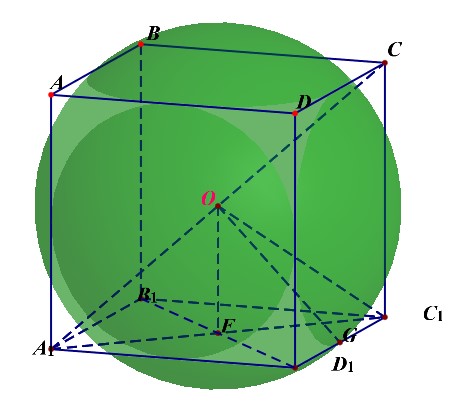
正方体的外接球的半径\(R_{外}=\cfrac{\sqrt{3}a}{2}=OC_1\);
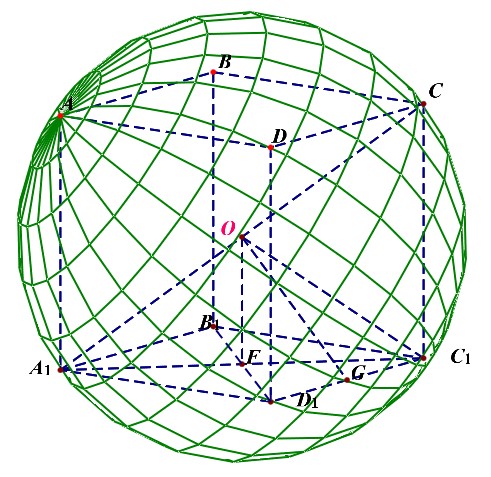
- 切面球半径\(R_{内}\)、切棱球半径\(R_{棱}\)、切点球半径\(R_{外}\)三者之比为\(1:\sqrt{2}:\sqrt{3}\);
球体与正六面体的切接
- 动画验证如下
典型例题
提示:可以转化为正方体的内切球问题,设内切球的半径为 \(R\),则 \(2R=6\),即 \(R=3\) ,
故 \(V_{\max}=V_{内切球}=\cfrac{4}{3}\pi R^3=36\pi\) \(cm^3\) .
提示:可以转化为正方体的外接球问题,设外接球的半径为 \(R\),则 \(R=\cfrac{\sqrt{3}a}{2}\),
故 \(V_{外接球}=\cfrac{4}{3}\pi R^3=\cfrac{\sqrt{3}}{2}\pi a^3\) \(cm^3\) .
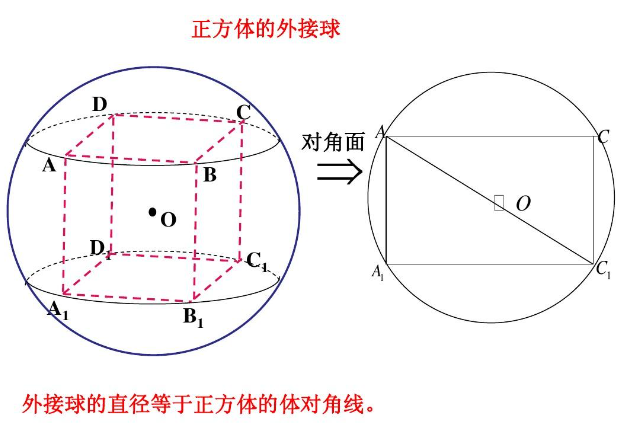

![球体与正六面体[正方体]切接](https://images.cnblogs.com/cnblogs_com/wanghai0666/1784871/o_20080714333219735190_22.jpg) 主要整理球体与正方体[正六面体]的切接问题
主要整理球体与正方体[正六面体]的切接问题
