向量的线性表示 | 习题

前言

向量的加法、减法、数乘运算称为向量的线性运算 .

典例剖析

【2024高一专项】在正方形 \(ABCD\) 中，\(M\) 是 \(BC\) 的中点，若 \(\overrightarrow{AC}\)\(=\)\(\vec{m}\)，\(\overrightarrow{AM}\)\(=\)\(\vec{n}\)，则 \(\overrightarrow{BD}\) = 【\(\qquad\)】

$A.4\vec{m}-3\vec{n}$ $B.4\vec{m}+3\vec{n}$ $C.3\vec{m}-4\vec{n}$ $D.3\vec{m}+4\vec{n}$

分析：本题目其实就是以向量 \(\{\vec{m},\vec{n}\}\) 为基底，来线性表示向量 \(\overrightarrow{BD}\)，此时我们可以依托向量加法的三角形法则或者向量加法的平行四边形法则来表达所求向量，比如可以寻找向量 \(\overrightarrow{BD}\) 所在的三角形 \(\triangle BCD\)，用向量加法的三角形法则 \(\overrightarrow{BD}\)\(=\)\(\overrightarrow{BC}\)\(+\)\(\overrightarrow{CD}\) 来刻画向量\(\overrightarrow{BD}\) ，然后将向量 \(\overrightarrow{BC}\) 和 \(\overrightarrow{CD}\) 再慢慢朝基底向量靠拢，直到最后的结果中只含有基底向量，这样就完成了题目要求。

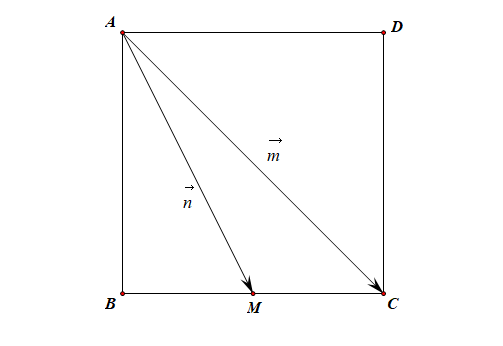
解 ： \(\overrightarrow{BD}\)\(=\)\(\overrightarrow{BC}\)\(+\)\(\overrightarrow{CD}\)

\(=2\overrightarrow{MC}+(\overrightarrow{AD}-\overrightarrow{AC})\)

\(=2\overrightarrow{MC}+2\overrightarrow{MC}-\vec{m}\)

\(=4\overrightarrow{MC}-\vec{m}\)

\(=4(\vec{m}-\vec{n})-\vec{m}\)

\(=3\vec{m}-4\vec{n}\)，故选 \(C\) .

【2024高一数学】在 \(\triangle ABC\) 中，\(D\) 是 \(BC\) 的中点，点 \(E\) 在 \(AD\) 上，且 \(\overrightarrow{AE}\)\(=\)\(3\overrightarrow{ED}\)，则 \(\overrightarrow{AE}\) = 【\(\qquad\)】

$A.\cfrac{1}{2}\overrightarrow{AB}+\cfrac{1}{2}\overrightarrow{AC}$ $B.\cfrac{1}{2}\overrightarrow{AB}+\cfrac{3}{8}\overrightarrow{AC}$ $C.\cfrac{3}{8}\overrightarrow{AB}+\cfrac{3}{8}\overrightarrow{AC}$ $D.\cfrac{3}{8}\overrightarrow{AB}+\cfrac{1}{2}\overrightarrow{AC}$

提示： 选 \(C\) ，希望能牢记向量加法的三角形法则的常用结论：\(\overrightarrow{AD}=\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})\)

【2024高一数学】在平行四边形 \(OADB\) 中，设 \(\overrightarrow{OA}=\vec{a}\)，\(\overrightarrow{OB}=\vec{b}\)，\(\overrightarrow{BM}\)\(=\cfrac{1}{3}\overrightarrow{BC}\)，\(\overrightarrow{CN}\)\(=\cfrac{1}{3}\overrightarrow{CD}\)，试用\(\vec{a}\)，\(\vec{b}\) 表示\(\overrightarrow{OM}\)，\(\overrightarrow{ON}\) 和 \(\overrightarrow{MN}\)，

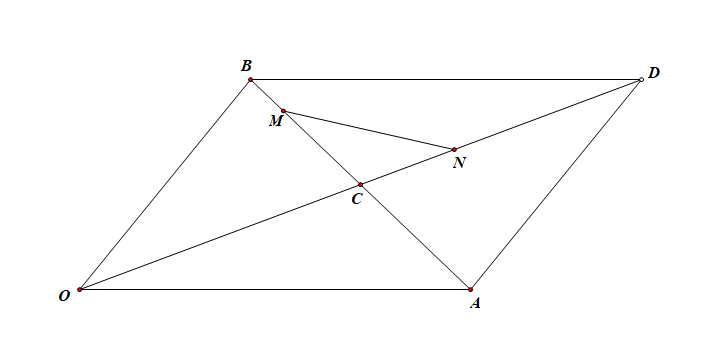
解：\(\overrightarrow{OM}\)\(=\)\(\overrightarrow{OC}\)\(+\)\(\overrightarrow{CM}\) ^[1]

\(=\cfrac{1}{2}(\vec{a}+\vec{b})+\cfrac{2}{3}\overrightarrow{CB}\)

\(=\cfrac{1}{2}(\vec{a}+\vec{b})+\cfrac{2}{3}\cdot\cfrac{1}{2}\overrightarrow{AB}\)

\(=\cfrac{1}{2}(\vec{a}+\vec{b})+\cfrac{1}{3}\overrightarrow{AB}\)

\(=\cfrac{1}{2}(\vec{a}+\vec{b})+\cfrac{1}{3}(\overrightarrow{OB}-\overrightarrow{OA})\)

\(=\cfrac{1}{2}(\vec{a}+\vec{b})+\cfrac{1}{3}(\vec{b}-\vec{a})\)

\(=\cfrac{1}{6}\vec{a}+\cfrac{5}{6}\vec{b}\)

\(\overrightarrow{ON}\)\(=\)\(\overrightarrow{OC}\)\(+\)\(\overrightarrow{CN}\)

\(=\cfrac{1}{2}\overrightarrow{OD}+\cfrac{1}{3}\overrightarrow{CD}\)

\(=\cfrac{1}{2}\overrightarrow{OD}+\cfrac{1}{3}\cdot\cfrac{1}{2}\overrightarrow{OD}\)

\(=\cfrac{2}{3}\overrightarrow{OD}\)\(=\cfrac{2}{3}(\overrightarrow{OA}+\overrightarrow{OB}\)

\(=\cfrac{2}{3}\vec{a}+\cfrac{2}{3}\vec{b}\)

\(\overrightarrow{MN}\)\(=\)\(\overrightarrow{CN}\)\(-\)\(\overrightarrow{CM}\)

\(=\cfrac{1}{6}\overrightarrow{OD}-\cfrac{1}{3}\overrightarrow{AB}\)

\(=\cfrac{1}{6}(\vec{a}+\vec{b})-\cfrac{1}{3}(\vec{b}-\vec{a})\)

\(=\cfrac{1}{2}\vec{a}-\cfrac{1}{6}\vec{b}\)

【2019届高三理科数学二轮用题】在矩形\(ABCD\)中，\(AB=2\)，\(AD=4\)，\(AC\)与\(BD\)相交于点\(O\)，过点\(A\)作\(AE\perp BD\)于\(E\)，则\(\overrightarrow{AE}\cdot \overrightarrow{AC}\)=【\(\qquad\)】

$A.\cfrac{8}{5}$ $B.\cfrac{16}{5}$ $C.\cfrac{32}{5}$ $D.8$

解法1️⃣ ：本题目可以用基向量法，以\(\overrightarrow{AB}\)和\(\overrightarrow{AD}\)为基向量来表示其他向量，

由射影定理可知，\(AB^2\)\(=\)\(BE\)\(\cdot\)\(BD\)，又 \(BD\)\(=\)\(2\)\(\sqrt{5}\)，故 \(BE\)\(=\)\(\cfrac{2\sqrt{5}}{5}\)，

令 \(\overrightarrow{BE}\)\(=\)\(t\)\(\overrightarrow{BD}\)，则 \(t\)\(=\)\(\cfrac{|\overrightarrow{BE}|}{|\overrightarrow{BD}|}\)\(=\)\(\cfrac{1}{5}\)，^[2]

又 \(\overrightarrow{AE}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\overrightarrow{BE}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{5}\)\(\overrightarrow{BD}\)

\(=\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{5}\)\((\overrightarrow{BA}\)\(+\)\(\overrightarrow{AD})\)

\(=\)\(\cfrac{4}{5}\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{5}\)\(\overrightarrow{AD}\)

又 \(\overrightarrow{AC}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\overrightarrow{AD}\)，

则 \(\overrightarrow{AE}\)\(\cdot\)\(\overrightarrow{AC}\)\(=\)\((\cfrac{4}{5}\overrightarrow{AB}\)\(+\)\(\cfrac{1}{5}\overrightarrow{AD}\))(\(\overrightarrow{AB}\)\(+\)\(\overrightarrow{AD}\))\(=\)\(\cfrac{4}{5}\overrightarrow{AB}^2\)\(+\)\(\cfrac{1}{5}\overrightarrow{AD}^2\)

\(=\cfrac{4}{5}\)\(\times\)\(4\)\(+\)\(\cfrac{4}{5}\)\(\times\)\(4\)\(=\)\(\cfrac{32}{5}\)， 故选 \(C\) .

解法2️⃣ ：从形的角度思考，采用坐标法求解；以点\(A\)为坐标原点建立如图所示的直角坐标系，

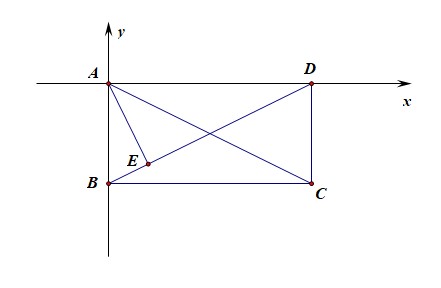
则可知 \(A(0，0)\)，\(B(0，-2)\)，\(C(4，-2)\)，\(D(4，0)\)，设 \(E(x，y)\)，

则由\(k_{AE}\)\(\cdot\)\(k_{BD}\)\(=\)\(-1\)，可得\(y\)\(=\)\(-2x\)①，又直线\(BD\)：\(2y\)\(=\)\(x-4\)②，

联立①②可得，\(x\)\(=\)\(\cfrac{4}{5}\)，\(y\)\(=\)\(-\cfrac{8}{5}\)，

则\(\overrightarrow{AE}\)\(\cdot\)\(\overrightarrow{AC}\)\(=\)\((\cfrac{4}{5}，-\cfrac{8}{5})\)\(\cdot\)\((4，-2)\)\(=\)\(\cfrac{32}{5}\)，故选 \(C\) .

---

1. 此处选取 \(\triangle OMC\) 的原因是，当\(\overrightarrow{OM}\)\(=\)\(\overrightarrow{OC}\)\(+\)\(\overrightarrow{CM}\) 拆解完成后，下一步 \(\overrightarrow{OC}\) 蕴含在向量加法的平行四边形法则中对角线向量\(\overrightarrow{OD}\)[可以用共起点的两个向量的和来表达]中，\(=\cfrac{1}{2}(\vec{a}+\vec{b})\)，\(\overrightarrow{CM}\) 蕴含在向量加法的平行四边形法则中对角线向量\(\overrightarrow{AB}\)[可以用共起点的两个向量的差来表达]中，这样很快就可以完成所求向量的线性表示。 ↩︎

2. 此处是先给等式取模长，由 \(\overrightarrow{BE}\)\(=\)\(t\)\(\overrightarrow{BD}\)，得到 \(|\overrightarrow{BE}|\)\(=\)\(|t|\)\(|\overrightarrow{BD}|\)，然后变形求 \(t\) 的值，不能理解为向量的除法，我们没有定义向量的除法，只定义了向量的加法、减法、数乘向量和向量的乘法运算； ↩︎