互为反函数问题

前言

本博文简单介绍反函数，对于学生而言，只需要知道同底数的指数函数 \(f(x)=a^x\) 与对数函数 \(g(x)=\log_ax\) (\(a>0\) 且 \(a\neq 1\)) 互为反函数就可以了，不需要知道如何求解给定函数的反函数，这个知识点在2005-2008年左右是个重难点考点。

典例剖析

已知常数 \(m\in R\)，若函数 \(f(x)=2^{x-m}\) 的反函数 \(g(x)\) 的图象经过点 \((4,2)\)，则 \(m=\)__________ .

法1：由于 \(g(x)\) 的图象经过点 \((4,2)\)，且 \(f(x)\) 与 \(g(x)\) 关于 直线 \(y=x\) 对称，

故 \(f(x)\) 的图象经过点 \((2,4)\)，代入 \(f(x)\) 得到，

\(2^{2-m}=4\)，解得 \(m=0\) .

法2：[求反函数法，供学有余力的学生使用]，由 \(y=f(x)=2^{x-m}\) 得到，

\(x-m=log_2y\)，即 \(x=log_2y+m\)，

互换 \(x,y\) 得到，\(y=log_2x+m\)，

即 \(g(x)=log_2x+m\)，由 \(g(x)\) 的图象经过点 \((4,2)\)，

得到，\(log_24+m=2\)，解得 \(m=0\) .

判断：当 \(a>1\) 时， \(f(x)=a^x\) 与 \(g(x)=log_a x\) 的交点个数为 \(0\)，\(1\)，\(2\)个。

法1：首先，我们知道互为反函数的两个函数的图象关于直线 \(y=x\) 对称，若 函数 \(f(x)\) 与直线 \(y=x\) 有几个交点，则 函数 \(g(x)\) 也必与直线 \(y=x\) 有几个交点，且交点相同，故探究函数 \(f(x)\) 与 函数 \(g(x)\) 的交点个数等价于探究函数 \(f(x)\) 与 直线 \(y=x\) 的交点个数问题。

利用极限思想，当 \(a>1\) 时，函数 \(f(x)\) 为指数函数，若让 \(a\) 从大变小，这个变化情况我们不一定清楚，不妨换个思路，\(a\) 的下限为 \(1\) ，故想着让 \(a\) 从 \(1\) 变大，当 \(a=1\) 时，函数 \(f(x)\) 为常函数，当 \(a\) 稍微变大一点，此时 函数 \(f(x)\) 就变为指数函数，原来直线的左端向下，右端向上，直线变为曲线，此时指数函数的曲线 和 \(y=x\) 的直线 一定有两个交点，再让 \(a\) 变大，到一定时候曲线和直线的两个交点就变成了一个，即曲线和直线相切，交点变为一个，若再让 \(a\) 变大，曲线和直线相离，交点变为零个，故 当 \(a>1\) 时， \(f(x)=a^x\) 与 \(g(x)=log_a x\) 的交点个数为 \(0\)，\(1\)，\(2\)个。

法2：计算法，首先将探究函数 \(f(x)\) 与 函数 \(g(x)\) 的交点个数等价转化为探究函数 \(f(x)\) 与 直线 \(y=x\) 的交点个数问题。 即求解方程 \(a^x=x\)的解的个数问题，两边取自然对数也即 \(x\ln a=\ln x\)，也即 \(\ln a=\cfrac{\ln x}{x}\) 的交点个数问题，这样又转换到形了。

以下用导数方法，判断函数\(g(x)=\cfrac{lnx}{x}\)的单调性，得到在\((0，e)\)上单调递增，在\((e，+\infty)\)上单调递减，做出其函数图像如图所示，

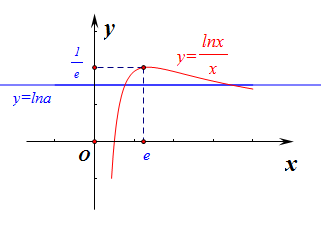
由图可知，当 \(0<\ln a<\cfrac{1}{e}\)，即 \(ln1<lna<lne^{\frac{1}{e}}\)，即 \(a\in (1，e^{\frac{1}{e}})\) 时， \(\ln a=\cfrac{\ln x}{x}\) 的交点为 \(2\) 个，

当 \(lna=\cfrac{1}{e}\)，即 \(lna=lne^{\frac{1}{e}}\)，即 \(a=e^{\frac{1}{e}}\) 时， \(\ln a=\cfrac{\ln x}{x}\) 的交点为 \(1\) 个，

当 \(lna>\cfrac{1}{e}\)，即 \(lna>lne^{\frac{1}{e}}\)，即 \(a\in (e^{\frac{1}{e}},+\infty)\) 时， \(\ln a=\cfrac{\ln x}{x}\) 的交点为 \(0\) 个，

综上所述，当 \(a>1\) 时， \(f(x)=a^x\) 与 \(g(x)=log_a x\) 的交点个数为 \(0\)，\(1\)，\(2\)个。

已知 \(\alpha\)，\(\beta\) 分别是 \(\log_2x+x-5=0\) 和 \(2^x+x-5=0\) 的根，则 \(\alpha+\beta=5\) .

分析：题目已知两个方程的根，你若此时想到用代数方法求解，那思路就太单一了。观察给定的方程发现，它们都是超越方程，是不能用代数方法求解的，故转换思路为从形的角度求解。这样将两个方程分别转化为 \(\log_2x\)\(=\)\(5-x\) 和 \(2^x\)\(=\)\(5-x\) ，将函数 \(y\)\(=\)\(log_2x\) 和函数 \(y\)\(=\)\(2^x\) 以及函数 \(y\)\(=\)\(5-x\) 画在同一个和坐标系中，则函数 \(y\)\(=\)\(log_2x\) 和函数 \(y\)\(=\)\(5-x\) 的交点横坐标为 \(\alpha\)，函数 \(y\)\(=\)\(2^x\) 和函数 \(y\)\(=\)\(5-x\) 的交点横坐标为 \(\beta\)，又由于 \(y\)\(=\)\(x\) 和 \(y\)\(=\)\(5-x\) 的交点为 \((2.5,2.5)\)，故 \(\cfrac{\alpha+\beta}{2}\)\(=\)\(2.5\)，即 \(\alpha\)\(+\)\(\beta\)\(=\)\(5\) .

【宝鸡市二检文理科第12题】已知函数\(f(x)=a^x\)与\(g(x)=log_ax(a>0且a \neq 1)\)的图像有两个公共点，则实数\(a\)的取值范围是【\(\quad\)】

$A.(0，e^{\frac{1}{e}})$ $B.(1，e^{\frac{2}{e}})$ $C.(1，\sqrt{e})$ $D.(1，e^{\frac{1}{e}})$

分析：先做出如右图所示的图像，从形上分析，由于函数\(f(x)=a^x\)与\(g(x)=log_ax(a>0且a \neq 1)\)互为反函数，其图像关于直线\(y=x\)对称，

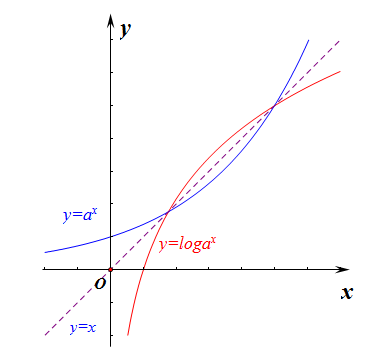
故两条曲线相交时，直线\(y=x\)必然也会过他们的交点，这样我们将图形简化一下，

即要保证两条曲线有两个交点，只需要一区一直两条线有两个交点就可以了，

此时我们从形上已经不好把握了，需要转换到数的角度进行计算。

即函数\(y=a^x\)与函数\(y=x\)的图像有两个交点，也即方程\(a^x=x\)要有两个不同的实数根。

两边同时取自然对数，得到\(lna^x=lnx\)，即\(xlna=lnx\)，注意到图像的交点的\(x\neq 0\)，

故分离参数得到\(lna=\cfrac{lnx}{x}\)，

则要方程使\(lna=\cfrac{lnx}{x}\)有两个不同的根，需要函数\(y=lna\)和\(g(x)=\cfrac{lnx}{x}\)要有两个交点，这样又转换到形了。

以下用导数方法，判断函数\(g(x)=\cfrac{lnx}{x}\)的单调性，得到在\((0，e)\)上单调递增，在\((e，+\infty)\)上单调递减，做出其函数图像如右图所示，

故有\(0<lna<\cfrac{1}{e}\)，即\(ln1<lna<lne^{\frac{1}{e}}\)，故\(a\in (1，e^{\frac{1}{e}})\)，选\(D\).

解后反思：

①、数到形，形到数，二者之间的转换在高三数学的学习中非常普遍。

②、熟练掌握函数\(f(x)=\cfrac{lnx}{x}\)，以及\(g(x)=lnx\pm x\)，\(h(x)=x\cdot lnx\)等的函数的图像和性质，在解题中会有不小的惊喜。

③、在分离常数时，可以分离得出\(lna=\cfrac{lnx}{x}\)，还可以分离得到\(a=e^{\frac{lnx}{x}}\)，但是明显第一种分离方式更有利于计算，此处使用了整体思想。

高阶提升

备注：以下内容仅供学有余力的学生使用，不是要求必须掌握的内容。

• 原函数在区间\([-a，a]\)上是单调函数，则一定存在反函数，且反函数也是单调函数[单调性和原函数相同]；原函数若存在反函数^[1]，但此函数不一定单调。[现行教材不要求掌握]

例如：函数\(f(x)=\begin{cases}-x & -1\leq x\leq 0\\x+1&0<x\leq 1\end{cases}\)是有反函数的，其反函数\(f^{-1}(x)=\begin{cases}-x & 0\leq x\leq 1\\x-1&1<x\leq 2\end{cases}\)，但是其反函数不单调；

---

1. 不是所有的函数都有反函数，比如 \(f(x)=x^2\)， \(x\in R\) 就没有反函数，联系函数的概念，多对一是函数，但是反过来就是一对多，就不是函数了，针对现行高中阶段的教材，仅仅学习到这里就可以了。 ↩︎