烧脑问题收集

前言

求解思路比较独特，故做以收集。

典例剖析

已知 \(a\)，\(b\)，\(c\)，\(d\) 是正整数，\(a^3=b^2\)，\(c^5=d^4\)，\(c-a=77\)，则 \(d-b=\) ?

解：由 \(a^3=b^2\)，变形得到 \(a\cdot a^2=b^2\)，故 \(a=\cfrac{b^2}{a^2}\)；

同理，由 \(c^5=d^4\)，变形得到 \(c\cdot c^4=d^4\)，故 \(c=\cfrac{d^4}{c^4}\)；

又由 \(c-a=77\)，即 \(\cfrac{d^4}{c^4}-\cfrac{b^2}{a^2}=77\)，则 \((\cfrac{d^2}{c^2})^2-(\cfrac{b}{a})^2=77\)

故 \((\cfrac{d^2}{c^2}+\cfrac{b}{a})\cdot(\cfrac{d^2}{c^2}-\cfrac{b}{a})=77=11\times7\)， ^[1]

又由于 \(\cfrac{d^2}{c^2}+\cfrac{b}{a}>\cfrac{d^2}{c^2}-\cfrac{b}{a}\)，故得到方程组如下：

\(\left\{\begin{array}{l}{\cfrac{d^2}{c^2}+\cfrac{b}{a}=11 ①}\\{\cfrac{d^2}{c^2}-\cfrac{b}{a}=7 ②}\end{array}\right.\quad\)

\(① + ②\) 得到，\(d^2=9c^2\)，则 \(d=3c\)，

\(① - ②\) 得到，\(b=2a\)，

由 \(c^5=d^4\)，则 \(c^5=81c^4\)，解得 \(c=81\)，

由 \(c-a=77\)，解得 \(a=4\)，则 \(b=8\)，\(d=3\times81=243\)，

故 \(d-b=243-8=235\) .

【2024高一联考题】“奔驰定理” 因其对应的几何图形酷似某汽车品牌标志而得名，它是平面向量中一个非常优美的结论 . 该定理与三角形四心(重心、内心、外心、垂心)有着神秘的关联，定理的具体视频讲解内容是: 如图，已知 \(M\) 是 \(\triangle ABC\) 内一点， \(\triangle BMC\), \(\triangle AMC\), \(\triangle AMB\) 的面积分别为 \(S_A\), \(S_B\), \(S_C\), 则有 \(S_A\cdot\overrightarrow{MA}\)\(+\)\(S_B\cdot \overrightarrow{MB}\)\(+\)\(S_C\cdot \overrightarrow{MC}\)\(=\)\(\vec{0}\) 成立 . 根据题意， 以下命题中正确的有 【\(\qquad\)】

$A$.若$S_A:S_B:S_C$=$1:1:1$, 则$M$为$\triangle$$ABC$的重心

$B.$若$M$为$\triangle ABC$的内心 ,则$BC$$\cdot$$\overrightarrow{MA}$$+$$AC$$\cdot$$\overrightarrow{MB}$$+$$AB$$\cdot$$\overrightarrow{MC}$$=$$\vec{O}$.

$C.$若$\angle BAC=45^{\circ}$ ,$\angle ABC=60^{\circ}$,$M$为$\triangle ABC$的外心 , 则$S_A:S_B:S_C$$=$$3:2:1$

$D.$$M$为$\triangle ABC$的垂心, $3\overrightarrow{MA}+4\overrightarrow{MB}+5\overrightarrow{MC}=\vec{O}$, 则$\cos\angle AMB=-\cfrac{\sqrt{6}}{6}$.

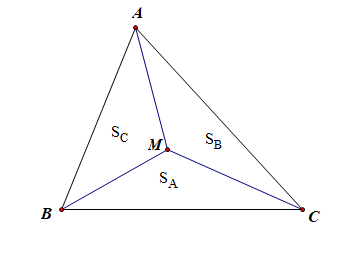
解析： 对于选项 \(A\) 而言，如图，由 \(S_A\cdot\overrightarrow{MA}\)\(+\)\(S_B\cdot \overrightarrow{MB}\)\(+\)\(S_C\cdot \overrightarrow{MC}\)\(=\)\(\vec{0}\) ，且 \(S_A:S_B:S_C\)=\(1:1:1\)，令 \(S_A=S_B=S_C=k\)，代入已知条件，约分得到，

则 \(\overrightarrow{MA}\)\(+\)\(\overrightarrow{MB}\)\(+\)\(\overrightarrow{MC}\)\(=\)\(\vec{0}\) ，则 \(M\) 为三角形的重心。故 \(A\) 正确；

对于选项 \(B\) 而言，由于点 \(M\) 为\(\triangle\)\(ABC\)的内心， 是三角形的三条角平分线的交点，如图，

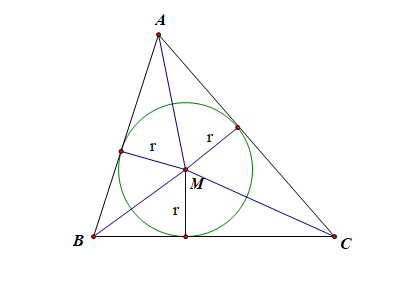
由 \(S_A\cdot\overrightarrow{MA}\)\(+\)\(S_B\cdot \overrightarrow{MB}\)\(+\)\(S_C\cdot \overrightarrow{MC}\)\(=\)\(\vec{0}\) ，

又 \(S_A=\cfrac{1}{2}BC\times r\)，\(S_B=\cfrac{1}{2}AC\times r\)，\(S_C=\cfrac{1}{2}AB\times r\)，

即 \(\cfrac{1}{2}BC\times r\times\cdot\overrightarrow{MA}\)\(+\)\(\cfrac{1}{2}AC\times r\times\cdot \overrightarrow{MB}\)\(+\)\(\cfrac{1}{2}AB\times r\times\cdot \overrightarrow{MC}\)\(=\)\(\vec{0}\) ，约分整理得到，

\(BC\)\(\cdot\)\(\overrightarrow{MA}\)\(+\)\(AC\)\(\cdot\)\(\overrightarrow{MB}\)\(+\)\(AB\)\(\cdot\)\(\overrightarrow{MC}\)\(=\)\(\vec{O}\)，故 \(B\) 正确；

对于选项 \(C\) 而言，由于点 \(M\) 为\(\triangle\)\(ABC\)的外心，则点 \(M\) 为三条边的中垂线的交点，且 \(MA\)\(=\)\(MB\)\(=\)\(MC\)\(=\)\(R\)，如图由 \(\angle1\)\(+\)\(\angle2\)\(=\)\(75^{\circ}\)， \(\angle2\)\(+\)\(\angle3\)\(=\)\(45^{\circ}\)， \(\angle1\)\(+\)\(\angle3\)\(=\)\(60^{\circ}\)，可以求得 \(\angle1\)\(=\)\(45^{\circ}\)， \(\angle2\)\(=\)\(30^{\circ}\)， \(\angle3\)\(=\)\(15^{\circ}\)，故 \(\angle\)\(BMC\)\(=\)\(90^{\circ}\)，\(\angle\)\(CMA\)\(=\)\(120^{\circ}\)，\(\angle\)\(AMB\)\(=\)\(150^{\circ}\)，

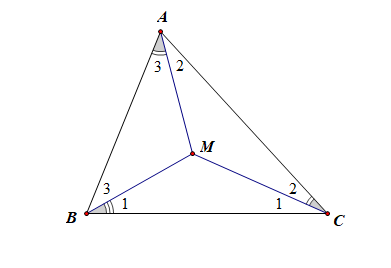
则由三角形面积公式可知，\(S_{A}=\cfrac{1}{2}\times R^2\times\sin 90^{\circ}\)，

\(S_{B}=\cfrac{1}{2}\times R^2\times\sin 120^{\circ}\)，\(S_{C}=\cfrac{1}{2}\times R^2\times\sin 150^{\circ}\)，

故 \(S_{A}:S_{B}:S_{C}=\sin 90^{\circ}:\sin 120^{\circ}:\sin 150^{\circ}=1:\cfrac{\sqrt{3}}{2}:\cfrac{1}{2}=2:\sqrt{3}:1\)，故 \(C\) 错误；

对于选项 \(D\) 而言，由于点 \(M\) 为\(\triangle\)\(ABC\)的垂心，是三角形的三条高线的交点，如图，

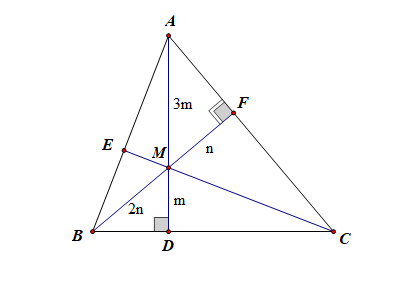
由题目\(S_A\cdot\overrightarrow{MA}\)\(+\)\(S_B\cdot \overrightarrow{MB}\)\(+\)\(S_C\cdot\overrightarrow{MC}\)\(=\)\(\vec{0}\) ，又\(3\overrightarrow{MA}\)\(+\)\(4\overrightarrow{MB}\)\(+\)\(5\overrightarrow{MC}\)\(=\)\(\vec{0}\)，则可知 \(S_A:S_B:S_C\)=\(3:4:5\)，故 \(\cfrac{S_{A}}{S_A+S_B+S_C}\)\(=\)\(\cfrac{3}{3+4+5}\)\(=\)\(\cfrac{1}{4}\)，故 \(\cfrac{MD}{AD}\)\(=\)\(\cfrac{1}{4}\)，同理可得， \(\cfrac{MF}{BF}\)\(=\)\(\cfrac{1}{3}\)，故可设，\(MD=m\)，\(AM=3m\)，\(MF=n\)，\(BM=2n\)，

在 \(Rt\triangle BMD\) 中，由 \(\cos\angle BMD=\cfrac{m}{2n}=\cos\angle AMF=\cfrac{n}{3m}\)，故得到 \(3m^2=2n^2\)，即 \(n=\cfrac{\sqrt{6}}{2}m\)，

则 \(\cos\angle BMD=\cfrac{m}{2n}=\cfrac{\sqrt{6}}{6}\)，故 \(\cos\angle AMB=\cos(\pi-\angle BMD)=-\cfrac{\sqrt{6}}{6}\) . 故 \(D\) 正确；

综上所述，选 \(ABD\)；

---

1. 当然，也可以这样分解 \(77=77\times1\)，仿照题目的求解思路，得到 \(d^2=39c^2\)，即 \(d=\sqrt{39}c\)，不符合 \(a\)，\(b\)，\(c\)，\(d\) 是正整数的要求，故这种分解 \(77=77\times1\)就排除了。 ↩︎