函数的周期性的作用

前言

函数的周期性到底对研究函数有什么作用？

https://aka.ms/edge/workspaceslaunch?code=dHlwZT0xJmlkPWFIUjBjSE02THk5b2IyMWxMbTFwWTNKdmMyOW1kSEJsY25OdmJtRnNZMjl1ZEdWdWRDNWpiMjB2T25VNkwyY3ZZMjl1ZEdWdWRITjBiM0poWjJVdk5rTjZibWxvVGpOMk1IVjVNWHBMTlVaeVVrTmlkelF4TURWak5EazRNVFZtWlRrMFlqUjNiM0pyYzNCaFkyVnpMMGxSU3poV056ZHlMWEpRTkZKS1lqRnZlR00xTkdKa1drRmtOWGswYkUxM1pVc3hNVXhPV2xSVmVERjZVa1ZGJnN0b3JlPTUmc291cmNlPVdvcmtzcGFjZXMmcmVkZWVtQ29kZT1kdW1teV9zZWVkJmFwcElkR3VpZD1iNmQ4MzNjZi1iNTRlLTRjYWItODE0My0xMzE4ZTBiYzUwZTE%3D&source=Workspaces

作用列举

做函数的图象

由 \(y=\sin x\)， \(x\in[0,2\pi]\) 的图像拓展到 \(y=\sin x\)， \(x\in R\) 的图像，就是利用的函数的周期的作用。

解三角不等式，常常是涉及有周期性的函数；

比如求解不等式的思路：\(\sin x >\cfrac{1}{2}\)，更多参阅

首先，这是超越不等式，不能使用代数方法求解，应该使用图像来求解，而涉及到图像时，由于函数 \(y=\sin x\) 有周期性，故分两步走，先选定一个周期[比如 \([0,2\pi]\)]，在这个周期内求解不等式的解集[在周期内的解集为 \((\cfrac{\pi}{6},\cfrac{5\pi}{6})\)]，然后将其拓展到 \(x\in R\) 上[在整个定义域内的解集为 \((2k\pi+\cfrac{\pi}{6},2k\pi+\cfrac{5\pi}{6})\)]\((k\in Z)\)。

求函数的解析式

【人教2019版教材\(P_{214}\) 第\(18\)题】已知函数 \(y=f(x)(x\in R)\)是周期函数，周期为 \(2\)，其部分图象如图所示 .

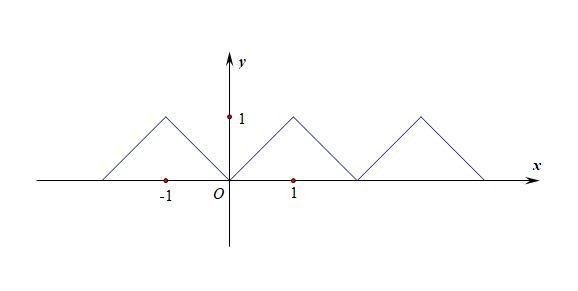
(1). 写出函数 \(y=f(x)\) 的解析式；

由于题目告诉我们周期为 \(2\)，故选 \([-1,1]\) 为一个周期，当 \(x\in[-1,1]\) 时的解析式为 \(y=|x|\)，再根据函数 \(y=f(x)\) 的图象和周期性，得到函数 \(y=f(x)\) 的解析式为 \(y=|x-2k|\)，此时，必须是 \(x\in[2k-1,2k+1]\)，\(k\in Z\) .

说明：本题目的解析式不唯一，也可以为 \(y=|x+2k|\)，则此时必须是 \(x\in[-2k-1,-2k+1]\)，\(k\in Z\) .

备注：当解析式确定为 \(y=|x-2k|\)时，说明是将 \(y=|x|\) 向左右平移周期 \(2\) 的整数倍，对应的自变量的取值区间也就变成了 \(x\in[2k-1,2k+1]\)，\(k\in Z\) .

(2). 画出函数 \(y=f(x+1)\) 的图象；

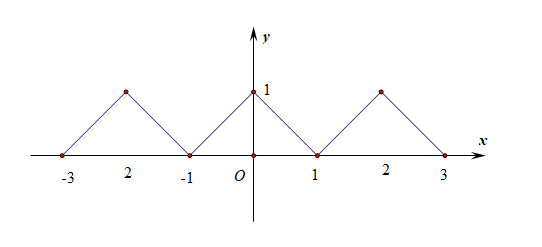
求函数的特殊值

已知\(f(x+1)\)是周期为 \(2\) 的奇函数，且当\(-1\leq x\leq 0\)时，\(f(x)=-2x(x+1)\)，且\(f(-\cfrac{3}{2})\)的值为_______.

分析：由于函数 \(f(x+1)\) 是奇函数，故\(f(-x+1)=-f(x+1)\)，即\(f(-x+1)+f(x+1)=0\)，

故函数\(f(x)\)关于点\((1，0)\)对称，则有\(f(x)+f(2-x)=0\)，即\(f(2-x)=-f(x)\)，

又函数 \(f(x+1)\) 是周期为 \(2\) 的周期函数，故 \(f(x)\) 也是周期为 \(2\) 的周期函数，

则有\(f(2-x)=f(-x)\)，故\(f(-x)=-f(x)\)，即函数\(f(x)\)为奇函数，

\(f(-\cfrac{3}{2})=-f(\cfrac{3}{2})=-f(\cfrac{3}{2}-2)=-f(-\cfrac{1}{2})=2\cdot(-\cfrac{1}{2})(-\cfrac{1}{2}+1)=-\cfrac{1}{2}\)。