平面向量习题|低阶
前言
当我们引入了用坐标刻画向量后,向量就既有形的表示[有向线段],也有数的表达[坐标],那么向量的位置关系也就能用数的形式来刻画了。比如给定向量 \(\vec{a}=(x_1,y_1)\), \(\vec{b}=(x_2,y_2)\), 则
向量的垂直关系可以表示为:
向量的平行关系可以表示为:
这样,我们常常会碰到利用向量的位置关系来求解坐标中包含参数的问题。当然还得注意,两个向量的共线等价于两个向量的平行。
典例剖析
(1). 求 \(\vec{a}\) 与 \(\vec{b}\) 的夹角的余弦值;
解析: 令 \(<\vec{a},\vec{b}>=\theta\),由于 \(\vec{a}=(4,-3)\) , \(\vec{b}=(5,0)\),
又由 \(\vec{a}\cdot\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot\cos\theta\),得到,\(\cos\theta=\cfrac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\)
则 \(\cos\theta=\cfrac{4\times 5+(-3)\times 0}{\sqrt{4^2+(-3)^2}\cdot\sqrt{5^2+0^2}}=\cfrac{20}{5\times 5}=\cfrac{4}{5}\) .
(2). 若向量 \(\vec{a}+k\vec{b}\) 与 \(\vec{a}-k\vec{b}\) 互相垂直, 求实数 \(k\) 的值;
解析: 由于 \(\vec{a}+k\cdot\vec{b}=(4+5k,-3)\), \(\vec{a}-k\cdot\vec{b}=(4-5k,-3)\),
又由于 \(\vec{a}+k\cdot\vec{b}\) 与 \(\vec{a}-k\cdot\vec{b}\) 垂直,则 \((\vec{a}+k\cdot\vec{b})\cdot\)\((\vec{a}-k\cdot\vec{b})=0\),
故 \((4+5k)(4-5k)+(-3)\times(-3)=0\), 即 \(16-25k^2+9=0\),
即 \(25-25k^2=0\) , 则 \(k=\pm 1\) .
(3). 当 \(k\) 为何值时, \(k\vec{a}+\vec{b}\) 与 \(\vec{a}-2\vec{b}\) 共线。
解析: \(k\vec{a}+\vec{b}=(4k+5,-3k+0)\), \(\vec{a}-2\vec{b}=(4-10,-3-2\times 0)=(-6,-3)\),
由于 \(k\vec{a}+\vec{b}\) 与 \(\vec{a}-2\vec{b}\) 共线,则 \((4k+5)\times(-3)-(-3k)\times(-6)=0\),
即\(-30k-15=0\), 解得 \(k=-\cfrac{1}{2}\) .
提示:由题设可以得到,\(\lambda \overrightarrow{AB}=\overrightarrow{DE}\),故点\(E\)应该在\(DC\)上,然后以点\(A\)为坐标原点建系,则\(B(3,0)\),\(D(1,\sqrt{3})\),\(C(4,\sqrt{3})\),设\(E(x,\sqrt{3})\),
由\(\overrightarrow{AE}\cdot \overrightarrow{BD}=0\),可解得\(x=\cfrac{3}{2}\),代入\(\lambda \overrightarrow{AB}=\overrightarrow{DE}\),求得\(\lambda=\cfrac{1}{6}\),故选\(A\).
提示:给\(|\vec{a}-\vec{b}|=1\)平方,可以求得\(\vec{a}\cdot \vec{b}\)的值,然后给\(|2\vec{a}+\vec{b}|\)平方再开方,可得;选\(D\).
提示:令\(|\vec{a}|=|\vec{b}|=t\),给\(|\vec{a}+\vec{b}|=\sqrt{3}|\vec{b}|\)平方,变形得到\(cos<\vec{a},\vec{b}>=\cfrac{1}{2}\),故\(<\vec{a},\vec{b}>=\cfrac{\pi}{3}\);
(1).若\(\vec{a}//\vec{c}\),求\(\vec{c}\)的坐标;
提示:设\(\vec{c}=(x,y)\),由题设得到方程组,求解即可,\(\vec{c}=(\sqrt{2},-3\sqrt{2})\)或\(\vec{c}=(-\sqrt{2},3\sqrt{2})\),
(2).若\(\vec{a}\perp (2\vec{a}-\vec{b})\),求\(\vec{a}\)与\(\vec{b}\)的夹角\(\theta\)。
提示:利用内积为\(0\),可以求得\(cos\theta=\cfrac{\sqrt{2}}{2}\),又\(\theta\in [0,\pi]\),故\(\theta=\cfrac{\pi}{4}\).
法1:将向量\(\vec{a}\),\(\vec{b}\)看成两个单个向量,设\(\vec{a}=(x,y)\),\(\vec{b}=(2,-1)\),
则\(\vec{a}+\vec{b}=(2+x,y-1)\),由\(\vec{a}+\vec{b}\)平行于\(x\)轴,可得\(y=1\)
由\(|\vec{a}+\vec{b}|=1\),可得到\(\sqrt{(2+x)^2+(1-1)^2}=1\),解得\(x=-1\)或\(x=-3\),
故\(\vec{a}=(-1,1)\)或\(\vec{a}=(-3,1)\).
法2:将\(\vec{a}+\vec{b}\)视为一个整体,由\(\vec{a}+\vec{b}\)平行于\(x\)轴,则\(\vec{a}+\vec{b}=(1,0)\)或\(\vec{a}+\vec{b}=(-1,0)\);
当\(\vec{a}+\vec{b}=(1,0)\)时,\(\vec{a}=(1,0)-\vec{b}=(1,0)-(2,-1)=(-1,1)\);
当\(\vec{a}+\vec{b}=(-1,0)\)时,\(\vec{a}=(-1,0)-\vec{b}=(-1,0)-(2,-1)=(-3,1)\);
法1:主动建系,利用向量的坐标,从数的角度计算;
由于不共线的平面向量\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)两两所成的角相等,即为\(\cfrac{2\pi}{3}\),
故建立如下所示的平面直角坐标系,则\(\vec{a}=(0,1)\),\(\vec{b}=(-\sqrt{3},-1)\),\(\vec{c}=(\cfrac{3\sqrt{3}}{2},-\cfrac{3}{2})\),
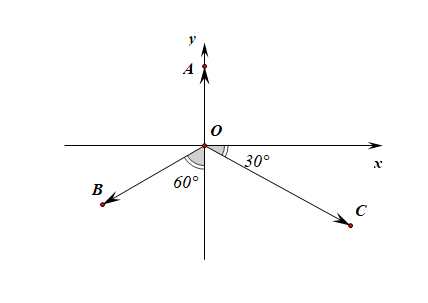
则\(\vec{d}=\vec{a}+\vec{b}+\vec{c}=(\cfrac{\sqrt{3}}{2},-\cfrac{3}{2})\),即\(\vec{d}=\sqrt{3}\);
设\(<\vec{d},\vec{a}>=\theta\),则由\(\cos\theta=\cdots=-\cfrac{\sqrt{3}}{2}\),解得\(\theta=\cfrac{5\pi}{6}\);
同理同法,可得到\(<\vec{d},\vec{b}>=\cfrac{\pi}{2}\),\(<\vec{d},\vec{c}>=\cfrac{\pi}{6}\).
故向量\(\vec{a}+\vec{b}+\vec{c}\)的长度为\(\sqrt{3}\),与三个向量的夹角分别为\(\cfrac{5\pi}{6}\)、\(\cfrac{\pi}{2}\)、\(\cfrac{\pi}{6}\).
法2:无需建系,利用已知的模长和已知的夹角求解;
由题目可知,\(|\vec{a}|=1\),\(|\vec{b}|=2\),\(|\vec{c}|=3\),令\(\vec{d}=\vec{a}+\vec{b}+\vec{c}\);
且\(<\vec{a},\vec{b}>=<\vec{b},\vec{c}>=<\vec{c},\vec{a}>=120^{\circ}\),
则\(|\vec{a}+\vec{b}+\vec{c}|=\sqrt{(\vec{a}+\vec{b}+\vec{c})^2}\)
\(=\sqrt{|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2+2\vec{a}\cdot\vec{b}+2\vec{a}\cdot\vec{c}+2\vec{b}\cdot\vec{c}}\)
\(=\sqrt{1+4+9+2\times 1\times 2\times(-\cfrac{1}{2})+2\times 2\times 3\times(-\cfrac{1}{2})+2\times 1\times 3\times(-\cfrac{1}{2}) }=\sqrt{3}\)
\(\cos<\vec{d},\vec{a}>=\cfrac{\vec{a}\cdot(\vec{a}+\vec{b}+\vec{c})}{|\vec{a}+\vec{b}+\vec{c}|\cdot \vec{a}}=\cfrac{\vec{a}\cdot\vec{a}+\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}}{\sqrt{3}\times 1}\)
\(=\cfrac{1+(-1)-\frac{3}{2}}{\sqrt{3}}=-\cfrac{\sqrt{3}}{2}\),故\(<\vec{d},\vec{a}>=\cfrac{5\pi}{6}\),
同理同法,可求其他的夹角,略。
法1:基向量法,即以向量 \(\overrightarrow{OA}\) 和 \(\overrightarrow{OB}\) 为基底,表达 向量 \(\overrightarrow{OC}\) 和 \(\overrightarrow{OM}\),再代入运算即可。
因为 \(\overrightarrow{OC}=\cfrac{1}{3}\overrightarrow{OA}+\cfrac{2}{3}\overrightarrow{OB}\),\(\overrightarrow{OM}=\cfrac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})\) ,
所以 \(\overrightarrow{OC}\cdot\overrightarrow{OM}=(\cfrac{1}{3}\overrightarrow{OA}+\cfrac{2}{3}\overrightarrow{OB})\cdot\cfrac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})\)
\(=\cfrac{1}{6}(\overrightarrow{OA}^{2}+2\overrightarrow{OB}^{2}+3\overrightarrow{OA}\cdot\overrightarrow{OB})\) ,
又 \(\triangle OAB\) 为等边三角形,所以 \(\overrightarrow{OA}\cdot\overrightarrow{OB}=2\times2\cos 60^{\circ}=2\) ,\(\overrightarrow{OA}^{2}=4\) ,\(\overrightarrow{OB}^{2}=4\) ,
所以 \(\overrightarrow{OC}\cdot\overrightarrow{OM}=3\) , 故选 \(D\) .
法2:特殊化策略,【考试中的首选方法】既然点 \(A\) 和点 \(B\) 都是圆上的动点为什么可以这样思考呢,由于点 \(C\) 和点 \(M\) 在线段 \(AB\) 上的位置都是相对于点 \(A\) 和点 \(B\) 都是相对确定的,这样 \(|\overrightarrow{OC}|\) 和 \(|\overrightarrow{OM}|\) 都是确定值,而且向量夹角也是确定值,故 \(\overrightarrow{OC}\cdot\overrightarrow{OM}\)应该是确定值,与夹角无关的,那么我们将点 \(A\) 放在最特殊的位置,应该是可以的,运算也简单,何乐而不为呢!,那么可以将点 \(A\) 放置在 \((2,0)\) 处,此时由于 \(|AB|=2\),则 \(\triangle OAB\)为等边三角形,故 点 \(B\) 可以放置在 点 \((1,\sqrt{3})\) 处,这样向量 \(\overrightarrow{OA}=(2,0)\) , \(\overrightarrow{OB}=(1,\sqrt{3})\) ,
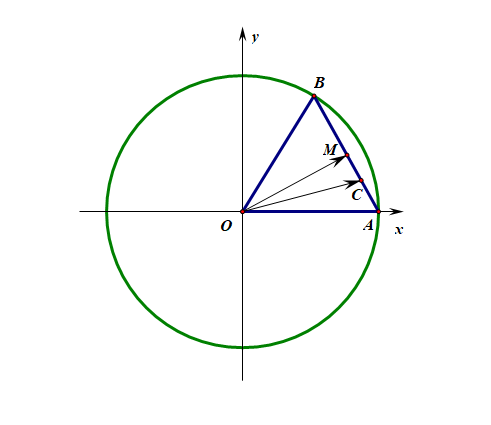
则 \(\overrightarrow{OC}\)\(=\)\(\cfrac{1}{3}\overrightarrow{OA}\)\(+\)\(\cfrac{2}{3}\overrightarrow{OB}\)\(=\)\(\cfrac{1}{3}(2,0)\)\(+\)\(\cfrac{2}{3}(1,\sqrt{3})\)\(=\)\((\cfrac{4}{3},\cfrac{2\sqrt{3}}{3})\) ,
又由于点 \(M\) 为 \(AB\) 的中点,故 \(M(\cfrac{3}{2},\cfrac{\sqrt{3}}{2})\),则 \(\overrightarrow{OM}\)\(=\)\((\cfrac{3}{2},\cfrac{\sqrt{3}}{2})\) ,
故 \(\overrightarrow{OC}\cdot\overrightarrow{OM}|=(\cfrac{4}{3},\cfrac{2\sqrt{3}}{3})\cdot(\cfrac{3}{2},\cfrac{\sqrt{3}}{2})=3\),故选 \(D\) .
法3:向量坐标法,如果上述的方法理解还是有疑虑,那么可以采用这个方法来计算打消我们的顾虑,就是运算比较麻烦。
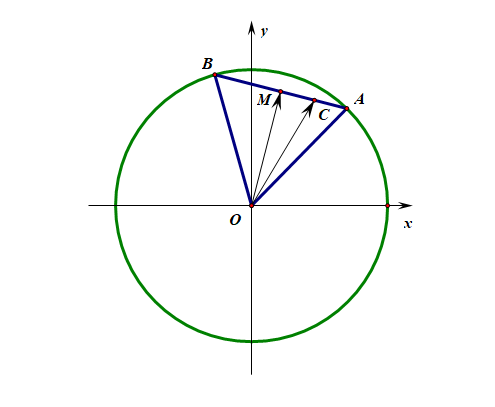
由于点 \(A\) 和点 \(B\) 都是圆上的动点,且 \(|AB|=2\) ,圆的半径也是 \(r=2\) ,故 \(\triangle OAB\)为等边三角形,利用圆的参数方程,令点 \(A(2\cos\theta,2\sin\theta)\),则点 \(B(2\cos(\theta+\cfrac{\pi}{3}),2\sin(\theta+\cfrac{\pi}{3}))\),这样
\(\overrightarrow{OA}\)\(=\)\((2\cos\theta,2\sin\theta)\) ,\(\overrightarrow{OB}\)\(=\)\((2\cos(\theta+\cfrac{\pi}{3}),2\sin(\theta+\cfrac{\pi}{3}))\) ,
\(\overrightarrow{OC}\)\(=\)\(\cfrac{1}{3}\overrightarrow{OA}\)\(+\)\(\cfrac{2}{3}\overrightarrow{OB}\)\(=\)\(\left(\cfrac{2}{3}\cos\theta+\cfrac{4}{3}\cos(\theta+\cfrac{\pi}{3}),\cfrac{2}{3}\sin\theta+\cfrac{4}{3}\sin(\theta+\cfrac{\pi}{3})\right)\) ,
\(\overrightarrow{OM}\)\(=\)\(\left(\cos\theta+\cos(\theta+\cfrac{\pi}{3}),\sin\theta+\sin(\theta+\cfrac{\pi}{3})\right)\) ,
故 \(\overrightarrow{OC}\cdot\overrightarrow{OM}\)\(=\)\(\left[\cfrac{2}{3}\cos\theta+\cfrac{4}{3}\cos(\theta+\cfrac{\pi}{3})\right]\)\(\left[\cos\theta+\cos(\theta+\cfrac{\pi}{3})\right]\)
\(+\)\(\left[\cfrac{2}{3}\sin\theta+\cfrac{4}{3}\sin(\theta+\cfrac{\pi}{3})\right]\)\(\left[\sin\theta+\sin(\theta+\cfrac{\pi}{3})\right]\)
\(=\)\(\cfrac{2}{3}\cos^2\theta\)\(+\)\(\cfrac{2}{3}\sin^2\theta\)\(+\)\(\cfrac{4}{3}\cos^2(\theta+\cfrac{\pi}{3})\)\(+\)\(\cfrac{4}{3}\sin^2(\theta+\cfrac{\pi}{3})\)
\(+\)\(\cfrac{2}{3}\left[\cos\theta\cos(\theta+\cfrac{\pi}{3})+\sin\theta\sin(\theta+\cfrac{\pi}{3})\right]\)\(+\)\(\cfrac{4}{3}\left[\cos\theta\cos(\theta+\cfrac{\pi}{3})+\sin\theta\sin(\theta+\cfrac{\pi}{3})\right]\)
\(=2+2\cos(\theta-\theta-\cfrac{\pi}{3})=2+1=3\),故选 \(D\) .
分析:设向量\(|\overrightarrow{AB}|=x\),则\(|\overrightarrow{OB}|=\sqrt{x^2+9}\),
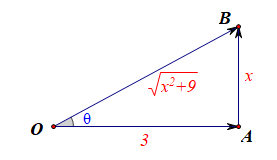
再设\(< \overrightarrow{OA} ,\overrightarrow{OB}>=\theta\),则\(\overrightarrow{OA}\cdot \overrightarrow{OB}=|\overrightarrow{OA}||\overrightarrow{OB}|cos\theta=3\times\sqrt{x^2+9}\times\cfrac{3}{\sqrt{x^2+9}}=9\)
【点评】根据内积的定义,要么求单个的\(|\overrightarrow{OB}|\)的值和\(cos\theta\)的值,要么能求得\(|\overrightarrow{OB}|cos\theta\)的整体的值,本题目刚好是利用三角函数能求得整体的值。
分析:由\(\vec{a}\cdot \vec{b}=0\),可知\(<\vec{a},\vec{b}>=90^{\circ}\),
又\(\vec{a}\cdot \vec{c}=\vec{b}\cdot \vec{c}=1\),即\(|\vec{a}||\vec{c}|cos<\vec{a},\vec{c}>=|\vec{b}||\vec{c}|cos<\vec{b},\vec{c}>=1\),
即\(<\vec{a},\vec{c}>=<\vec{b},\vec{c}>=45^{\circ}\),故由\(\vec{a}\cdot \vec{c}=1\)可知,
\(|\vec{c}|=\sqrt{2}\),又\(|\vec{a}|=1\),\(|\vec{b}|=1\),
则有\(|\vec{a}+\vec{b}+\vec{c}|^2=\vec{a}^2+\vec{b}^2+\vec{c}^2+2\vec{a}\cdot \vec{b}+2\vec{a}\cdot \vec{c}+2\vec{b}\cdot \vec{c}=1+1+2+0+2+2=8\),
故\(|\vec{a}+\vec{b}+\vec{c}|=2\sqrt{2}\)。
\(A.|\vec{a}\cdot \vec{b}|\leq |\vec{a}||\vec{b}|\)
分析:恒成立,由于\(\vec{a}\cdot \vec{b}=|\vec{a}|\cdot |\vec{b}|cos\theta\) ,故有\(|\vec{a}\cdot \vec{b}|=|\vec{a}|\cdot |\vec{b}||cos\theta|\leq |\vec{a}|\cdot |\vec{b}|\) ;
\(B.|\vec{a}- \vec{b}|\leq ||\vec{a}|-|\vec{b}||\)
分析:不恒成立,比如这个反例,\(\vec{a}=\vec{-b}\),取为一对相反单位向量,则此时左边为\(|2|\leq 0\)出错。
\(C.(\vec{a}+ \vec{b})^2= |\vec{a}+\vec{b}|^2\)
分析:恒成立,可以按照多项式乘法展开;
\(D.(\vec{a}+ \vec{b})\cdot (\vec{a}- \vec{b})= \vec{a}^2-\vec{b}^2\)
分析:恒成立,可以按照多项式乘法展开; 故选 \(B\) .
分析:求向量的内积的取值范围,应该想到用内积的坐标运算,本题目难点是一般想不到主动建系,由形的运算转化为数的运算。
解:如图所示,以点\(C\)为坐标原点,分别以\(CB、CA\)所在的直线为\(x、y\)轴建立如同所示的坐标系,
则\(C(0,0)\),\(A(0,3)\),\(B(3 ,0)\),设点\(N\)的横坐标为\(x\),则由等腰直角三角形可知,点\(N\)的纵坐标为\(3-x\),即点\(N(x,3-x)\),
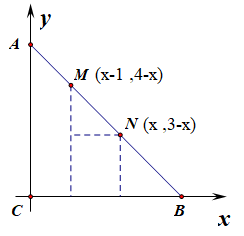
又由\(MN=\sqrt{2}\),计算可知点\(M(x-1,4-x)\),则\(\overrightarrow{CM}=(x-1,4-x)\),\(\overrightarrow{CN}=(x,3-x)\),
由于点\(M,N\)是动点,取两个极限位置研究\(x\)的取值范围,
当点\(M\)位于点\(A\)时,\(x\)取到最小值\(1\),当点\(N\)位于点\(B\)时,\(x\)取到最大值\(3\),即\(1\leq x\leq 3\),
则\(\overrightarrow{CM}\cdot \overrightarrow{CN}=f(x)=((x-1,4-x)\cdot (x,3-x)\)
\(=x(x-1)+(4-x)(3-x)=2(x-2)^2+4\),\(x\in [1,3]\)
当\(x=2\)时,\(f(x)_{min}=f(2)=4\),当\(x=1\)或\(x=3\)时,\(f(x)_{max}=f(1)=f(3)=6\),
即\(f(x)\in [4,6]\) . 故选\(D\) .
解析: 以 \(A\) 为坐标原点 \(AB\) 所在的直线为 \(x\) 轴建立平面直角坐标系如图所示.

则 \(A(0,0)\), \(B(3,0)\), \(C(-1, \sqrt{3})\),
由于 \(\overrightarrow{BD}=2\overrightarrow{DC}\), 所以 \(\overrightarrow{BD}=\cfrac{2}{3}\overrightarrow{BC}=\cfrac{2}{3}(-4,\sqrt{3})=(-\cfrac{8}{3},\cfrac{2\sqrt{3}}{3})\),
则 \(D(\cfrac{1}{3},\cfrac{2\sqrt{3}}{3})\), 则 \(\overrightarrow{AD}=(\cfrac{1}{3},\cfrac{2\sqrt{3}}{3})\),\(\overrightarrow{AB}=(3,0)\)
所以, \(\overrightarrow{AB}\cdot\overrightarrow{AD}=3\times\cfrac{1}{3}+0\times\cfrac{2\sqrt{3}}{3}=1\), 故选 \(B\) .
解法1️⃣ :从形的角度思考,采用坐标法求解;以点\(A\)为坐标原点建立如图所示的直角坐标系,
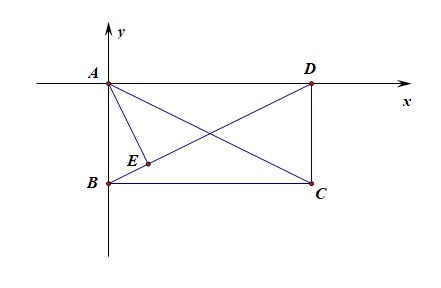
则可知 \(A(0,0)\),\(B(0,-2)\),\(C(4,-2)\),\(D(4,0)\),设 \(E(x,y)\),
则由\(k_{AE}\)\(\cdot\)\(k_{BD}\)\(=\)\(-1\),可得\(y\)\(=\)\(-2x\)①,又直线\(BD\):\(2y\)\(=\)\(x-4\)②,
联立①②可得,\(x\)\(=\)\(\cfrac{4}{5}\),\(y\)\(=\)\(-\cfrac{8}{5}\),
则\(\overrightarrow{AE}\)\(\cdot\)\(\overrightarrow{AC}\)\(=\)\((\cfrac{4}{5},-\cfrac{8}{5})\)\(\cdot\)\((4,-2)\)\(=\)\(\cfrac{32}{5}\),故选 \(C\) .
解法2️⃣ :本题目还可以用基向量法,以\(\overrightarrow{AB}\)和\(\overrightarrow{AD}\)为基向量来表示其他向量,
由射影定理可知,\(AB^2\)\(=\)\(BE\)\(\cdot\)\(BD\),又 \(BD\)\(=\)\(2\)\(\sqrt{5}\),故 \(BE\)\(=\)\(\cfrac{2\sqrt{5}}{5}\),
令 \(\overrightarrow{BE}\)\(=\)\(t\)\(\overrightarrow{BD}\),则 \(t\)\(=\)\(\cfrac{|\overrightarrow{BE}|}{|\overrightarrow{BD}|}\)\(=\)\(\cfrac{1}{5}\),[1]
又 \(\overrightarrow{AE}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\overrightarrow{BE}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{5}\)\(\overrightarrow{BD}\)
\(=\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{5}\)\((\overrightarrow{BA}\)\(+\)\(\overrightarrow{AD})\)
\(=\)\(\cfrac{4}{5}\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{5}\)\(\overrightarrow{AD}\)
又 \(\overrightarrow{AC}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\overrightarrow{AD}\),
则 \(\overrightarrow{AE}\)\(\cdot\)\(\overrightarrow{AC}\)\(=\)\((\cfrac{4}{5}\overrightarrow{AB}\)\(+\)\(\cfrac{1}{5}\overrightarrow{AD}\))(\(\overrightarrow{AB}\)\(+\)\(\overrightarrow{AD}\))\(=\)\(\cfrac{4}{5}\overrightarrow{AB}^2\)\(+\)\(\cfrac{1}{5}\overrightarrow{AD}^2\)
\(=\cfrac{4}{5}\)\(\times\)\(4\)\(+\)\(\cfrac{4}{5}\)\(\times\)\(4\)\(=\)\(\cfrac{32}{5}\), 故选 \(C\) .
综合提升
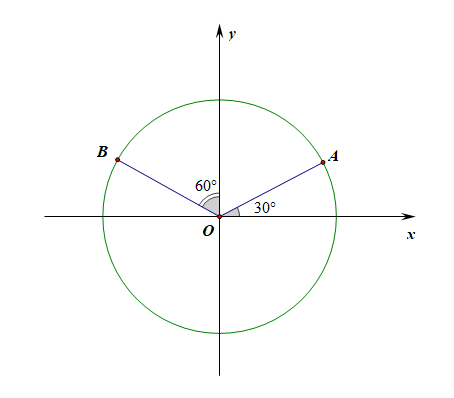
法1:向量法,由题目可知,\(\angle AOB=120^{\circ}\),\(|\overrightarrow{OA}|=|\overrightarrow{OB}|=1\),
则\(|2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{|2\overrightarrow{OA}+3\overrightarrow{OB}|^2}\)
\(=\sqrt{4|\overrightarrow{OA}|^2+9|\overrightarrow{OB}|^2+2\times 2\times 3\times \overrightarrow{OA}\cdot \overrightarrow{OB}}\)
\(=\sqrt{4+9+2\times 2\times 3\times 1\times 1\times (-\cfrac{1}{2})}=7\),故\(|2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{7}\)。
法2:坐标法,已知\(A(\cfrac{\sqrt{3}}{2},\cfrac{1}{2})\),\(B(-\cfrac{\sqrt{3}}{2},\cfrac{1}{2})\),则\(\overrightarrow{OA}=(\cfrac{\sqrt{3}}{2},\cfrac{1}{2})\),
\(\overrightarrow{OB}=(-\cfrac{\sqrt{3}}{2},\cfrac{1}{2})\),则\(2\overrightarrow{OA}+3\overrightarrow{OB}=(-\cfrac{\sqrt{3}}{2},\cfrac{5}{2})\),
故\(|2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{(-\cfrac{\sqrt{3}}{2})^2+(\cfrac{5}{2})^2}=\sqrt{7}\)。
法3:解三角形法,由向量的平行四边形法则可知,所求的模长即\(\triangle OCD\)中的边长\(|OC|\),由已知\(|OD|=3|OB|=3\),\(|CD|=2|OA|=2\),\(\angle ODC=60^{\circ}\),
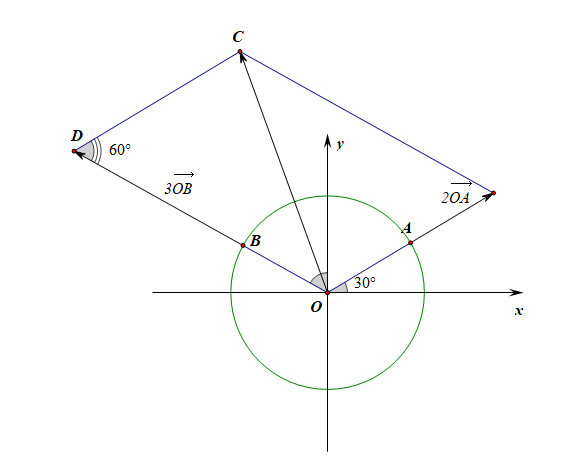
由余弦定理可知\(|2\overrightarrow{OA}+3\overrightarrow{OB}|^2=|OC|^2=2^2+3^2-2\times2\times 3\times cos60^{\circ}=7\),
故\(|2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{7}\)。
法1:基向量法,
\(|\vec{a}+2\vec{b}|^2=\vec{a}^2+4\vec{b}^2+2\times 2\times \vec{a}\cdot \vec{b}\);
\(=|\vec{a}|^2+4|\vec{b}|^2+4|\vec{a}|\cdot |\vec{b}|\cdot cos60^{\circ}\);
\(=1+16+4\times 1\times 2\times cos60^{\circ}=21\),
故\(|\vec{a}+2\vec{b}|=\sqrt{21}\)。
法2:建立坐标系,利用向量坐标法构造向量三角形法,
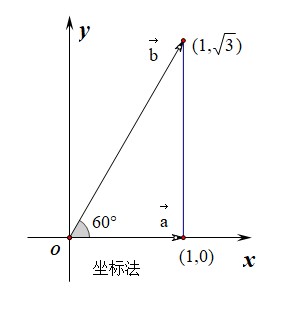
建立如图所示的坐标系,则可知\(\vec{a}=(1,0)\),\(\vec{b}=(1,\sqrt{3})\),
则\(\vec{a}+2\vec{b}=(1,0)+2(1,\sqrt{3})=(3,2\sqrt{3})\),
故\(|\vec{a}+2\vec{b}|=\sqrt{3^2+(2\sqrt{3})^2}=\sqrt{21}\)。
法3:构造向量三角形法,利用余弦定理求解。

由图可知,\(\overrightarrow{OA}=\vec{a}\),\(\overrightarrow{OD}=2\vec{b}\),做向量三角形\(\triangle OAB\),
则在\(\triangle OAB\)中,\(|OA|=|\vec{a}|=1\),\(|AB|=|2\vec{b}|=4\),\(|OB|=|\vec{a}+2\vec{b}|\),\(\angle OAB=120^{\circ}\),
由余弦定理可知,\(|OB|^2=1^2+4^2-2\times 1\times 4\times cos120^{\circ}=21\),
故\(|\vec{a}+2\vec{b}|=|OB|=\sqrt{21}\)。
高阶提升
此处是先给等式取模长,由 \(\overrightarrow{BE}\)\(=\)\(t\)\(\overrightarrow{BD}\),得到 \(|\overrightarrow{BE}|\)\(=\)\(|t|\)\(|\overrightarrow{BD}|\),然后变形求 \(t\) 的值,不能理解为向量的除法,我们没有定义向量的除法,只定义了向量的加法、减法、数乘向量和向量的乘法运算; ↩︎

 收集整理有关向量的低阶习题。
收集整理有关向量的低阶习题。

