
我们积累的数学知识越多,解题的思路就越开阔,越顺畅。
前言
在新人教 A 版的复数部分看到下述这个经典的题目,联想到以前的相应解法,现对各种思路作以总结,并体会一下:我们积累的数学知识越多,解题的思路就越开阔,越顺畅。
典例列举
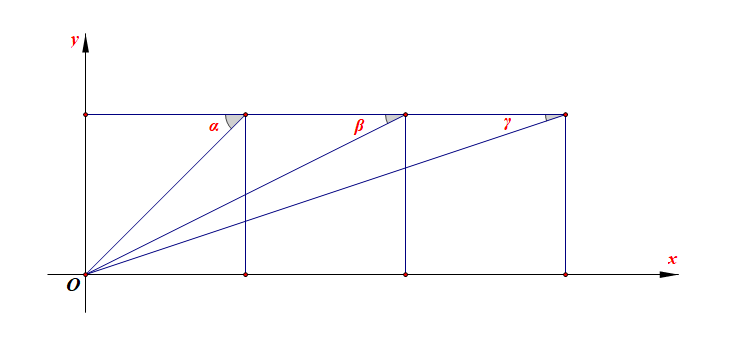
如图所示,已知平面内并列的三个相同大小的正方形,求证: α+β+γ=π2.
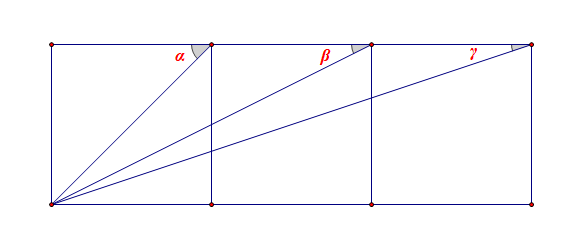
解法赏析
【法 1】:平面几何法 [考虑采用下移的方法],
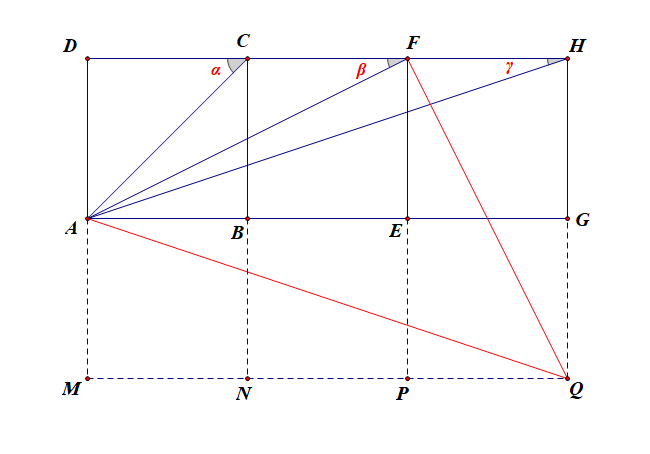
如图,向下平移三个并列放置的三个全等的正方形,得到大矩形 MQHD,连结 AQ 和 FQ,
则由图易知,α=π4,β=∠FAG=∠PFQ,γ=∠QAG,故有
∠AFQ=∠AFP+∠PFQ=∠AFP+β=∠DFP=π2
又由于 AF=QF,故 △AFQ 为等腰直角三角形,则 ∠FAQ=∠FQA=π4,
而 ∠FAQ=∠FAG+∠QAG=β+γ=π4,故证得 α+β+γ=π2.
【法 2】:相似三角形法;
连结 HE,则 ∠EHG=α,故只需证明 ∠AHE=β,
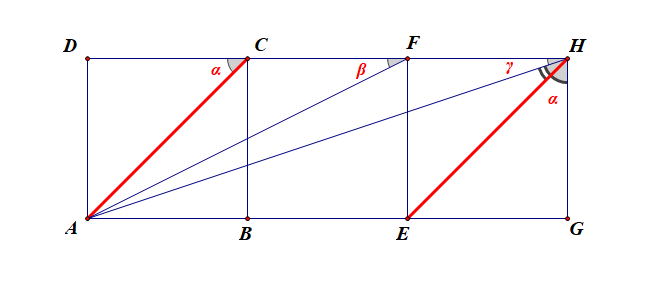
由题目可知 CF:AC:AF=1:√2:√5,EH:AE:AH=√2:2:√10,
故 EHCF=AEAC=AHAF=√2,故 △FCA∼△HEA,
故 ∠AHE=β,即可得 α+β+γ=π2.
【法 3】:三角函数法;
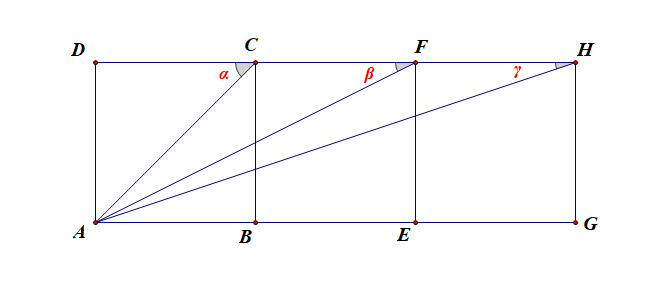
解证:显然 α=π4 , 故只需要求出 β+γ=π4,借助三角函数知识可知,
tanβ=12,tanγ=13,则由两角和的正切公式可知,
tan(β+γ)=tanβ+tanβ1−tanβ⋅tanγ=12+131−12×13=5656=1,
由题目可知,β,γ 都是锐角,故 β+γ=π4,
即可知 α+β+γ=π2.
【法 4】:复数法;新的高考改革对复数的内容和考察难度都有所增加,各位学子请务必注意;
本题目为何能使用复数的乘法来求解?
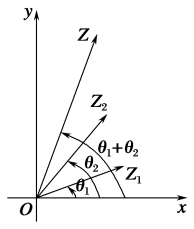
复数乘法的几何意义:两个复数 z1 ,z2 相乘时,可以如下图所示,先分别画出与 z1 ,z2 对应的向量 −−→OZ1, −−→OZ2,然后把向量 −−→OZ1 绕点 O 按逆时针方向旋转角 θ2(如果 θ2<0,就要把向量 −−→OZ1 绕点 O 按顺时针方向旋转角 |θ2| ),再把它的模变为原来的 r2 倍,得到向量 −−→OZ, −−→OZ 表示的复数就是积 z1⋅z2,这就是复数乘法的几何意义。
借助复数的代数形式以及对应的三角形式来解释,z1=a1+b1i=r1(cosθ1+isinθ1),z2=a2+b2i=r2(cosθ2+isinθ2),则
z=z1⋅z2=r1⋅r2[cos(θ1+θ2)+isin(θ1+θ2)]
简单来说,复数乘法有两个作用,其一放大或缩小的作用,体现在 r1⋅r2;其二旋转的作用,体现在 θ1+θ2。
由此可知,我们如果要求解 β+γ=π4,只需要验证 β、γ 分别对应的复数的乘积的辐角主值为 π4 即可,比如,
(2+i)(3+i)=5+5i
而 5+5i 的辐角主值为 π4 ,则说明 β+γ=π4 。
解证:建立如图所示的复平面,可知 α,β,γ 分别等于复数 1+i , 2+i , 3+i 的辐角主值,故 α+β+γ 的和取决于三个复数的乘积的辐角主值。由于
(1+i)(2+i)=2−1+3i=1+3i
(1+3i)(3+i)=3−3+10i=10i
即 (1+i)(2+i)(3+i)=10i,而复数 10i 的辐角主值就是 π2,故 α+β+γ=π2.
作者:陕西凤翔,微信:wh1979448597,邮箱:wanghai0666@126.com,敬请雅正,欢迎联系。
情怀:一直设想如何利用自己浅陋的教学感悟和粗鄙的电脑知识,将数学学习的手段和要素都整合到云端。
出处:https://www.cnblogs.com/wanghai0666/p/17098932.html
版权:本作品采用「署名 - 非商业性使用 - 相同方式共享 4.0 国际」许可协议进行许可。
题记:用数学的眼光观察世界,用数学的思维分析世界,用数学的语言表达世界!
声明:本博客版权归「静雅斋数学」所有。

 我们积累的数学知识越多,解题的思路就越开阔,越顺畅。
我们积累的数学知识越多,解题的思路就越开阔,越顺畅。









【推荐】国内首个 AI IDE,深度理解中文开发场景,立即下载体验 Trae
【推荐】编程新体验,更懂你的 AI,立即体验豆包 MarsCode 编程助手
【推荐】抖音旗下 AI 助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现
2020-02-15 交轨法