关注同理同法的重要性|思维+速度
在解题过程中碰到 “同理同法可得” 这样的关键词时需要特别注意感悟思考，到底同的什么算理，同的什么方法，这时候往往是拓展我们思维深度层次和提升运算速度的最佳契机。
前言
在理科[数学、物理、化学，尤其是数学这一工具学科中]的计算中，时不时会碰到相同的思路和算法的重复，这时候在解题过程中常常用 “同理同法可得” 这样的关键词，我们在学习时需要特别注意感悟思考，到底同的什么算理，同的什么方法，这时候往往是拓展我们思维深度层次和提升运算速度的最佳契机。借助以下几个案例，加以说明：
案例剖析
解析： 抛物线 \(x^{2}=y\) 的焦点为 \(F(0，\cfrac{1}{4})\) ，[用图形帮助大家理解本题目所采用的算理]
设直线 \(m\) 的倾斜角为 \(\alpha\) ，可得直线 \(m\) 的参数方程为 \(\left\{\begin{array}{l}x=0+t\cos\alpha ，\\y=\cfrac{1}{4}+t\sin\alpha\end{array}\right.\) ( \(t\) 为参数)，
代入抛物线的方程 \(x^{2}=y\) 得到关于\(t\)的一元二次方程 ， \(\cos^{2}\alpha\cdot t^2-\sin\alpha\cdot t-\cfrac{1}{4}=0\) ，
则其必然满足 \(\Delta=(-\sin\alpha)^2+\cos^2\alpha=1>0\)，设 \(P\)，\(Q\) 对应的参数分别为 \(t_{1}\)，\(t_{2}\) ，
则由韦达定理得到， \(t_{1}+t_{2}=\cfrac{\sin\alpha}{\cos^{2}\alpha}\) ， \(t_{1} t_{2}=-\cfrac{1}{4\cos^{2}\alpha}\) ，
则 \(|PQ|=|t_{1}-t_{2}|=\sqrt{(t_{1}+t_{2})^{2}-4 t_{1}t_{2}}\)
\(=\sqrt{\cfrac{\sin ^{2} \alpha}{\cos ^{4}\alpha}+\cfrac{1}{\cos ^{2} \alpha}}\)\(=\sqrt{\cfrac{\sin ^{2} \alpha+\cos ^{2} \alpha}{\cos ^{4} \alpha}}=\cfrac{1}{\cos ^{2} \alpha}\)
即有 \(|PQ|=\cfrac{1}{\cos^{2}\alpha}\) ，[如何计算\(|MN|\)才是这个题目的难点，同样的思路走一遍，必然费时费力]
将 \(\alpha\) 换为 \(\alpha+30^{\circ}\) ，同理由于计算 \(|MN|\) 的算理和计算方法和计算 \(|PQ|\) 的是完全一样的，二者不同的仅仅是倾斜角，这样我们就可以直接借助上述的结论得到我们想要的东西，而且能节省大量的时间和精力，更重要的是锤炼了我们的数学素养。不过需要注意此处的思维跳跃性还是很大的。需要我们平时有意识的加以练习。 可得 \(|MN|=\cfrac{1}{\cos^{2}\left(\alpha+30^{\circ}\right)}\) ，
则 \(\cfrac{1}{|P Q|}+\cfrac{1}{|M N|}=\cos ^{2} \alpha+\cos ^{2}\left(\alpha+30^{\circ}\right)\)
\(=\cfrac{1+\cos 2 \alpha}{2}+\cfrac{1+\cos \left[2\left(\alpha+30^{\circ}\right)\right]}{2}\)
\(=1+\cfrac{1}{2}\left[\cos 2 a+\cos \left(2 a+60^{\circ}\right)\right]\)
\(=1+\cfrac{1}{2}\left(\cfrac{3}{2} \cos 2 \alpha-\cfrac{\sqrt{3}}{2} \sin 2 \alpha\right)\)
\(=1+\cfrac{\sqrt{3}}{2} \cos \left(2 \alpha+30^{\circ}\right)\)
当 \(\cos \left(2 \alpha+30^{\circ}\right)=-1\) ，即 \(\alpha=75^{\circ}\) 时， \(\cfrac{1}{|PQ|}+\cfrac{1}{|MN|}\) 的最小值为 \(1-\cfrac{\sqrt{3}}{2}\).
〔解后反思〕：如果学校是代数、几何内容分开讲授，那么一看到抛物线和直线的相交问题，则学生很可能会想到设直线的点斜式方程，联立曲线方程利用弦长公式的思路来求解，从而由于运算量大而主动退却放弃；这一思维定势需要克服，同时需要深入体会参数方程在解决这一类问题的便利。
符号语言：\(\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}\)；
【思路一】：利用三角形的高证明正弦定理[易想易证]；
证明：(1).设\(\triangle ABC\)为锐角三角形时，设边\(AB\)上的高为\(CD\)，根据锐角三角函数定义可知，
有\(CD=a\cdot sinB\)；\(CD=b\cdot sinA\)；由此得到，\(\cfrac{a}{sinA}=\cfrac{b}{sinB}\)；
同理得到，\(\cfrac{b}{sinB}=\cfrac{c}{sinC}\)，故\(\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}\)在锐角三角形中成立；
(2).设\(\triangle ABC\)为钝角三角形时，过点\(C\)做边\(AB\)上的高，交\(AB\)的延长线于点\(D\)，根据锐角三角函数定义可知，
有\(CD=a\cdot sin\angle CBD=a\cdot sin\angle ABC\)；\(CD=b\cdot sinA\)；由此得到，\(\cfrac{a}{sinA}=\cfrac{b}{sinB}\)；
同理得到，\(\cfrac{b}{sinB}=\cfrac{c}{sinC}\)，故\(\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}\)在钝角三角形中成立；
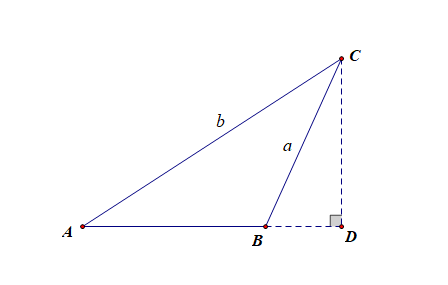
(3).当\(\triangle ABC\)为直角三角形时，比如\(C=\cfrac{\pi}{2}\)，容易验证\(\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}\)成立；
综上所述，在\(\triangle ABC\)中，一定有\(\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}\)；
【思路二】：利用三角形的面积证明正弦定理[易想易证]；
证明：如图在\(\triangle ABC\)中，边\(AB\)上的高为\(CD\)，则\(CD=a\cdot sinB\)，
则\(S_{\triangle ABC}=\cfrac{1}{2}\times AB\times CD=\cfrac{1}{2}acsinB\)；
同理可得到\(S_{\triangle ABC}=\cfrac{1}{2}absinC=\cfrac{1}{2}bcsinA\)；
则有\(acsinB=absinC=bcsinA\)，同除以\(abc\)，得到
\(\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}\)；
如图，已知：三棱锥\(O-ABC\)的三个侧面分别为\(\alpha\)，\(\beta\)，\(\gamma\)，且\(\alpha\perp\beta\)，\(\alpha\perp\gamma\)，\(\beta\perp\gamma\)，\(\alpha\cap\beta=m\)，\(\alpha\cap\gamma=l\)，\(\beta\cap\gamma=n\)，
求证：\(l\perp m\)，\(l\perp n\)，\(m\perp n\)，
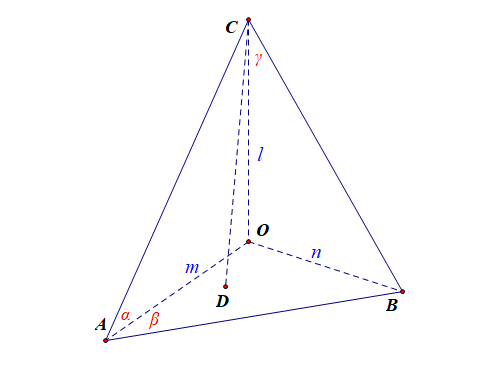
分析：[同一法]过点\(C\)做\(CD\perp \beta\)，垂足为点\(D\)，
由于点\(C\in l\)，点\(C\in \alpha\)，且\(\alpha\perp\beta\)，则\(D\in \alpha\)过一个平面的垂面内一点，做该平面的垂线，则垂线一定在该垂面内；\(\quad\)；
同理，点\(C\in l\)，点\(C\in \gamma\)，且\(\gamma\perp\beta\)，则\(D\in \gamma\)；
由于\(D\in \alpha\)，\(D\in \gamma\)，\(\alpha\cap\gamma=l\)，则点\(D\in l\)，
故点\(D\)和点\(O\)是同一个点，故\(CO\perp\beta\)，即\(l\perp\beta\)；
又\(m\in \beta\)，\(n\in \beta\)，则\(l\perp m\)，\(l\perp n\)，
同理可证\(n\perp m\)，\(n\perp l\)；
综上所述，\(l\perp m\)，\(l\perp n\)，\(m\perp n\)；
分析：在锐角三角形中，\(A，B，C\in (0，\cfrac{\pi}{2})\)，故\(A+B>\cfrac{\pi}{2}\)，
即\(A>\cfrac{\pi}{2}-B\)，此时可知\(A，\cfrac{\pi}{2}-B\in (0，\cfrac{\pi}{2})\)，
而函数\(y=sinx\)在区间\((0，\cfrac{\pi}{2})\)上单调递增，故\(sinA>sin(\cfrac{\pi}{2}-B)=cosB\)，
同理，\(sinB>cosC\)，\(sinC>cosA\)，三个式子相加得到，
\(sinA+sinB+sinC>cosA+cosB+cosC\)。
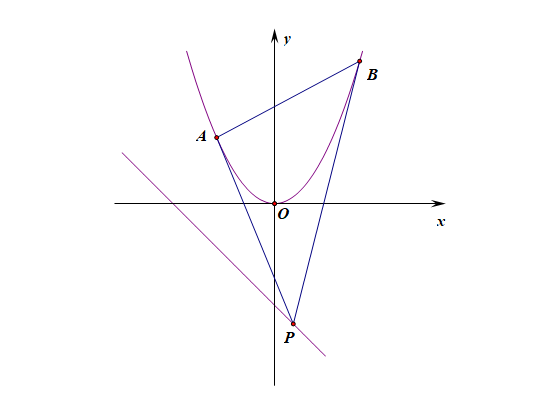
分析：由于点\(P\)在直线\(x+y+2=0\)上，故设\(P(-2-y_{0}, y_{0})\)，
又由于点\(A\)，\(B\)在\(y=x^{2}\)上，故设\(A(x_{1}, x_{1}^{2})\), \(B(x_{2}, x_{2}^{2})\)，
由于\(y^{\prime}=2x\)，则\(k_{1}=2x_{1}\)，则在\(A\)点的切线方程\(l_{1}\)为\(y-x_{1}^{2}=2x_{1}(x-x_{1})\)，
又由于点\(P\)在\(l_{1}\)上，则\(y_{0}-x_{1}^{2}=2 x_{1}(-2-y_{0}-x_{1})\)，即\(x_{1}^{2}+2(y_{0}+2)x_{1}+y_{0}=0\)，
同理， \(B\)点的切线方程有\(x_{2}^{2}+2(y_{0}+2)x_{2}+y_{0}=0\)，[仿上的结果直接写出，工作量减少一半]
所以，\(x_{1}\)，\(x_{2}\)是方程\(x^{2}+2(y_{0}+2)x+y_{0}=0\)的两根，[此处用到合二为一的策略]
由韦达定理可知，\(\left\{\begin{array}{l}x_{1}+x_{2}=-2(y_{0}+2)\\x_{1}x_{2}=y_{0}\end{array}\right.\)
则有\(\cfrac{y_{0}+y_{1}+y_{2}}{3}=\cfrac{x_{1} x_{2}+x_{1}^{2}+x_{2}^{2}}{3}\)
\(=\cfrac{x_{1} x_{2}+(x_{1}+x_{2})^2-2x_1x_2}{3}=\cfrac{(x_{1}+x_{2})^2-x_1x_2}{3}\)
\(=\cfrac{4(y_0+2)^2-y_0}{3}=\cfrac{4y_0^2+15y_0+16}{3}>0\) [\(\Delta=15^2-4\times4\times16<0\)]
故\(\triangle PAB\)的重心恒在\(x\)轴上方, 故选\(A\).
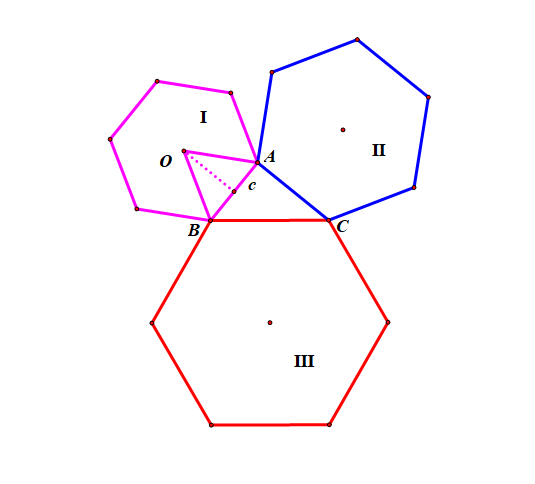
解析：由图可知，\(b^2+c^2=a^2\) 且有 \(S_{Ⅰ}=6\times\cfrac{1}{2}\times c\times\cfrac{\sqrt{3}}{2}c=\cfrac{3\sqrt{3}c^2}{2}\)，
同理，\(S_{Ⅱ}=\cfrac{3\sqrt{3}b^2}{2}\)，\(S_{Ⅲ}=\cfrac{3\sqrt{3}a^2}{2}\)，
又由于 \(S_{Ⅰ}+ S_{Ⅱ}=\cfrac{3\sqrt{3}c^2}{2}+\cfrac{3\sqrt{3}b^2}{2}=\cfrac{3\sqrt{3}}{2}(b^2+c^2)=\cfrac{3\sqrt{3}}{2}a^2=S_{Ⅲ}\)，
故所求概率为 \(P=\cfrac{S_{Ⅲ}}{S_{Ⅰ}+ S_{Ⅱ}+S_{Ⅲ}}=\cfrac{1}{2}\) 。
何时用到
对于同理同法的思路，什么命题会遇到呢？待后总结；
轮换对称性命题可能用到；并列型命题可能用到；
