构造函数中的套路剖析 | 同构构造
前言
同构构造,即构造相同的结构,这样就容易联系上函数的单调性 .
典例剖析
【分析】利用函数的单调性去掉绝对值符号,构造新函数,可以将问题再次转化为恒成立,然后分离参数求解。
【解答】不妨设\(m>n\),则函数\(f_1(x)\)在区间\([0,1]\)上单调递增,故\(f_1(m)-f_1(n)>0\),
又\(f_2(x)=a(x-1)^2+b-a\),对称轴是\(x=1\),开口向上,故函数\(f_2(x)\)在区间\([0,1]\)上单调递减,故\(f_2(m)-f_2(n)<0\),
这样对任意的\(m,n∈[0,1](m>n)\),\(|f_1(m)-f_1(n)|>|f_2(m)-f_2(n)|\)恒成立,
就可以转化为\(f_1(m)-f_1(n)>f_2(n)-f_2(m)\)恒成立,
即\(f_1(m)+f_2(m)>f_1(n)+f_2(n)\)恒成立,
令\(h(x)=f_1(x)+f_2(x)=e^x+ax^2-2ax+b\),则到此的题意相当于已知\(m >n\)时,\(h(m)>h(n)\),
故函数\(h(x)\)在区间\([0,1]\)上单调递增,故\(h'(x)≥0\)在区间\([0,1]\)上恒成立;
即\(h'(x)=e^x+2ax-2a≥0\)在区间\([0,1]\)上恒成立;
即\(2a(1-x)≤ e^x\)恒成立,这里我们使用倒数法分离参数得到,分离参数法
\(\cfrac{1}{2a}≥\cfrac{1-x}{e^x}\)在区间\([0,1]\)上恒成立;
再令\(p(x)=\cfrac{1-x}{e^x}\),即需要求\(p(x)_{max}\),
\(p'(x)=\cfrac{-1×e^x-(1-x)e^x}{(e^x)^2}=\cfrac{x-2}{e^x}\),
容易看出,当\(x∈[0,1]\)时,\(p'(x)<0\)恒成立,故\(p(x)\)在区间\([0,1]\)上单调递减,
则\(p(x)_{max}=p(0)=1\),故\(\cfrac{1}{2a}≥1\),又\(a>0\),
故解得 \(0<a\leqslant\cfrac{1}{2}\)。故\(a_{max}=\cfrac{1}{2}\).
【点评】出现函数值的差的绝对值问题,常常想到利用函数的单调性去掉绝对值符号进行转化;另外在分离参数时如果按照常规方法分离需要分类讨论,这里使用了倒数法分离参数,就能很好的避免分类讨论,嵌套的层次比较多,运算量比较多,是个难题。
解析:选 \(B\) . 理由如下:
由 \(f(x)+f(-x)+2x^2=0\) ,得到 \(f(x)+x^2=-f(-x)-(-x)^2\),令\(h(x)=f(x)+x^2\),则 \(h(x)=-h(-x)\),故 \(h(x)\) 为奇函数,
令 \(F(x)=f(x)+x^2-x\)此处涉及到构造函数的相关问题,如有兴趣,可参阅如下博文:
破解构造函数问题;
构造函数习题1;
构造函数习题2;
构造函数的难点和层次;
构造函数中的切入点;
再议构造函数;,则 \(F(x)=h(x)-x\),则\(F(x)\)为奇函数\(y\)\(=\)\(h(x)\)为奇函数,\(y\)\(=\)\(-x\)为奇函数,奇+奇=奇,是奇函数的一种比较常用的给出方式;,
由题目可知, 当\(x>0\) 时,\(F'(x)\)\(=\)\([f(x)+x^2-x]'\)\(=\)\(f'(x)\)\(+\)\(2x\)\(-1\)\(<0\)恒成立其目的是为了给出所构造的新函数的构造方向和将来构造的新函数的部分单调性,即函数 \(F(x)\) 在区间 \((0,+\infty)\)上单调递减,
又由于函数\(f(x)\)在 \(R\) 上存在导数为 \(f'(x)\)函数\(f(x)\)在 \(R\) 上可导,则函数 \(f(x)\) 必然在 \(R\) 上连续,从而导致 \(F(x)\) 在 \(R\) 上可导且连续,从而由 \(F(x)\) 在 \((0,+\infty)\) 上单调递减,可得到 \(F(x)\)必然会经过 \((0,0)\) 点,则会推知 \(F(x)\) 在 \([0,+\infty)\) 上单调递减,再结合其奇偶性就能知道在 \(R\) 上的单调性;,则函数\(f(x)\)在 \(R\) 上可导,则\(f(x)\)在 \(R\) 上连续,函数 \(F(x)\)在 \(R\) 上可导且连续,则函数 \(F(x)\) 在区间 \([0,+\infty)\)上单调递减,
又由于 函数 \(F(x)\) 为奇函数,则 在区间 \((-\infty,+\infty)\)上单调递减,
由 \(f(m)\geqslant f(1)-m^2+m\) 可得到, \(f(m)+m^2-m\geqslant f(1)\),即 \(f(m)+m^2-m\geqslant f(1)+1^2-1\),
即 \(F(m)\geqslant F(1)\),由于 \(F(x)\) 在 \(R\) 上单调递减,则可得到 \(m\leqslant 1\),则 \(m_{_{max}}=1\),故 选 \(B\) .
【解后反思】
①题目中给定对于任意实数 \(x\),都有 \(f(x)\)\(+\)\(f(-x)\)\(+\)\(2x^2\)\(=\)\(0\),是为了让我们构造函数 \(h(x)=f(x)+x^2\) 为奇函数;
②题目中给定[当\(x>0\) 时,\(f'(x)+2x<1\)],能得到构造的函数 \(F(x)\) 在区间 \((0,+\infty)\) 上单调递减[如图\(1\)所示,虽然定义在 \(R\) 上,但是在 \(R\) 上并不单调],并不能得到在区间 \([0,+\infty)\) 上单调递减,再结合条件[在函数\(f(x)\)在 \(R\) 上存在导数为 \(f'(x)\)],则可以得到在区间 \([0,+\infty)\) 上单调递减[如图\(2\)所示],再结合奇函数则可以得到在 \((-\infty,+\infty)\) 上单调递减;
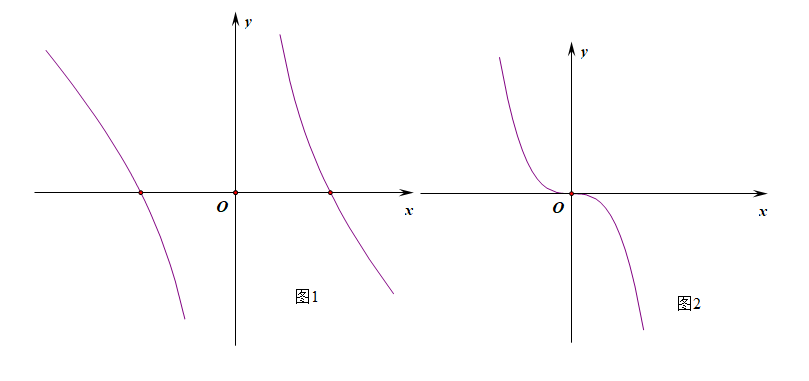
③函数在 \(R\) 上可导,则函数的图像在 \(R\) 上一定是连续的。
(1). 当 \(a=-4\) 时,求函数 \(f(x)\) 在区间 \([1,e]\) 上的最大值和相应的 \(x\) 值;
解:由题目可知,定义域为\((0,+\infty)\);
当\(a=-4\)时,\(f'(x)=\cfrac{-4}{x}+2x=\cfrac{2x^2-4}{x}=\cfrac{2(x-\sqrt{2})(x+\sqrt{2})}{x}\)
借助导函数的分子的图像和\(x\in [1,e]\),可知
当 \(x\in[1,\sqrt{2})\)时,\(f'(x)<0,f(x)\searrow\);当 \(x\in(\sqrt{2},e]\)时,\(f'(x)>0,f(x)\nearrow\);
又因为端点值\(f(1)=1\),\(f(e)\)\(=\)\(e^2-4\)\(>\)\(f(1)\),
故\(x=e\)时,\(f(x)_{max}\)\(=\)\(f(e)\)\(=\)\(e^2-4\).
(2). 当 \(x\in [1,e]\) 时,讨论方程 \(f(x)=0\) 的根的个数;
解:当 \(x=1\) 时,方程 \(f(x)=alnx+x^2=0\) 无解;当 \(x>1\) 时,\(lnx>0\),
故方程 \(f(x)=0\) 的根的个数即就是方程 \(-a=\cfrac{x^2}{lnx}\) 的根的个数,
即函数 \(g(x)=-a\) 和函数 \(h(x)=\cfrac{x^2}{lnx}\) 的图像的交点个数。
又 \(h'(x)\)\(=\)\(\cfrac{2xlnx-x^2\cdot\cfrac{1}{x}}{ln^2x}\)\(=\)\(\cfrac{x(2lnx-1)}{ln^2x}\),
借助导函数的分子的图像得到:\(x\in(1,\sqrt{e})\)时,\(h'(x)<0,h(x)\searrow\);
\(x\in(\sqrt{e},e)\)时,\(h'(x)>0,h(x)\nearrow\);又\(h(\sqrt{e})=2e,h(e)=e^2\),
在同一个坐标系中作出函数\(g(x)\)和\(h(x)\)的图像可知,
\(1^。\)当\(-a<2e\)时,即\(a>-2e\)时,两个函数图像没有交点,原方程无解;
\(2^。\)当\(-a=2e\)时,即\(a=-2e\)时,两个函数图像有一个交点,原方程一个解;
\(3^。\)当\(2e<-a\leq e^2\)时,即\(-e^2\leq a<-2e\)时,两个函数图像有两个交点,原方程有两个解;
\(4^。\)当\(-a>e^2\)时,即\(a<-e^2\)时,两个函数图像有一个交点,原方程一个解;
综上所述:
当\(a>-2e\)时,原方程根的个数是0个;
当\(a<-e^2\)或\(a=-2e\)时,原方程根的个数是1个;
当\(-e^2\leq a<-2e\)时,原方程根的个数有2个;
(3). 若 \(a>0\),且对 \(\forall\)\(x_1\),\(x_2\)\(\in\)\([1,e]\),都有 \(|f(x_1)\)\(-\)\(f(x_2)|\)\(\leq\)\(|\cfrac{1}{x_1}\)\(-\)\(\cfrac{1}{x_2}|\),求实数 \(a\) 的取值范围。
解析:当 \(a>0\)时,\(f'(x)\)\(=\)\(\cfrac{a}{x}+2x\)\(>0\),即函数 \(f(x)\) 在 \(x\in [1,e]\) 上单增,
又函数 \(y=\cfrac{1}{x}\) 在 \(x\in [1,e]\) 上单减,不妨设 \(1\leq x_1<x_2\leq e\),
则 \(|f(x_1)\)\(-\)\(f(x_2)|\)\(\leq\)\(|\cfrac{1}{x_1}\)\(-\)\(\cfrac{1}{x_2}|\) 等价于 \(f(x_2)\)\(-\)\(f(x_1)\)\(\leq\)\(\cfrac{1}{x_1}\)\(-\)\(\cfrac{1}{x_2}\),
即 \(f(x_1)\)\(+\)\(\cfrac{1}{x_1}\)\(\ge\)\(f(x_2)\)\(+\)\(\cfrac{1}{x_2}\) 在 \(x\in [1,e]\) 上恒成立,
令 \(g(x)\)\(=\)\(f(x)\)\(+\)\(\cfrac{1}{x}\)\(=\)\(a\ln x\)\(+\)\(x^2\)\(+\)\(\cfrac{1}{x}\),则原命题等价于函数 \(g(x)\) 在区间 \(x\in [1,e]\) 上单调递减,
所以 \(g'(x)\)\(=\)\(\cfrac{a}{x}\)\(+\)\(2x\)\(-\)\(\cfrac{1}{x^2}\)\(\leq\)\(0\) 在 \(x\)\(\in\)\([1,e]\) 上恒成立;分离参数得到 \(a\)\(\leq\)\(\cfrac{1}{x}\)\(-\)\(2x^2\) 在 \(x\)\(\in\)\([1,e]\) 上恒成立;
又 \(h(x)\)\(=\)\(\cfrac{1}{x}\)\(-\)\(2x^2\) 在 \(x\)\(\in\)\([1,e]\) 上单调递减,则\(h(x)_{min}\)\(=\)\(h(e)\)\(=\)\(\cfrac{1}{e}-2e^2\);所以\(a\)\(\leq\)\(\cfrac{1}{e}\)\(-\)\(2e^2\)
又由题目可知 \(a>0\),故 \(a\)\(\in\)\(\varnothing\),即满足条件的实数 \(a\) 不存在 .
分析:本题中的题眼是在\((0,+\infty)\)上\(f'(x)<x\),这句话是构造函数的关键所在。
解析: 构造函数\(g(x)=f(x)-\cfrac{1}{2}x^2\),[1]
则在 \((0,+\infty)\) 上 \(g'(x)=f'(x)-x<0\),即 \(g(x)\) 单调递减,
又由于 \(f(-x)\)\(+\)\(f(x)\)\(=\)\(x^2\),将其等价变形为 \(f(-x)\)\(-\)\(\cfrac{1}{2}(-x)^2\)\(+\)\(f(x)\)\(-\)\(\cfrac{1}{2}(x)^2\)\(=\)\(0\),
即就是 \(g(-x)\)\(+\)\(g(x)\)\(=\)\(0\),则函数 \(g(x)\) 为定义在 \(R\) 上的奇函数,
由上可知当 \((0,+\infty)\) 时, \(g(x)\) 单调递减,则 \((-\infty,0)\) 上也单调递减,
所以函数 \(g(x)\) 在 \((-\infty,+\infty)\) 上单调递减。
又由于 \(f(4-m)-f(m)\)\(\ge\)\(8\)\(-\)\(4m\),等价变形为 \(f(4-m)\)\(-\)\(\cfrac{1}{2}(4-m)^2\)\(\ge\)\(f(m)\)\(-\)\(\cfrac{1}{2}m^2\),[2]
即等价于 \(g(4-m)\) \(\ge\) \(g(m)\),所以\(4-m\)\(\leq\)\(m\),解得\(m\)\(\ge\)\(2\),即\(m\)\(\in\)\([2,\infty)\).
⑴. 令\(F(x)=x\cdot f(x)-g(x)\),求\(F(x)\)的单调区间;
解:由于 \(g(x)\) 是分段函数,故按道理求 \(F(x)\) 也应该是分段函数,但是 \(f(x)\) 的定义域是 \((0,+\infty)\),故 \(F(x)\) 也应该定义在\((0,+\infty)\) 上,
故 \(F(x)=xlnx-\cfrac{1}{2}x^2\),则\(F'(x)=lnx+1-x=lnx-(x-1)=f(x)-h(x)\),到此可以考虑两个思路:
思路一,从形上入手分析,利用函数 \(y=f(x)\) 和 \(h(x)=x-1\) 的图像很快的看出\(F'(x)\)的正负,这两个函数的图像的相互位置应该是常识性的东西,需要理解记忆;
故当 \(0<x<1\) 时,\(F'(x)<0\);当 \(x>1\) 时,\(F'(x)<0\);当 \(x=1\) 时,\(F'(x)=0\);
即\(x\in (0,+\infty)\)时,\(F'(x)\leq 0\)恒成立,即函数\(F(x)\)只有单调递减区间\((0,+\infty)\)。
思路二,从数上入手分析,构造函数\(G(x)\)\(=\)\(F'(x)\)\(=\)\(\ln x\)\(+\)\(1-x\),则\(G'(x)\)\(=\cfrac{1}{x}\)\(-\)\(1\),
由 \(G'(x)\)\(=\)\(\cfrac{1}{x}\)\(-\)\(1>0\),得到\(0<x<1\);由\(G'(x)=\cfrac{1}{x}-1<0\),得到\(x>1\);
即\(G(x)\)在\((0,1)\)上为增函数,在\((1,+\infty)\)上为减函数,
即\(F'(x)\)在\((0,1)\)上为增函数,在\((1,+\infty)\)上为减函数,故\(F'(x)\leq F'(1)=0\),
故函数\(F(x)\)在区间\((0,+\infty)\)上单调递减,没有单调递增区间 。
⑵. 若任意\(x_1\),\(x_2\)\(\in\)\([1,+\infty)\),且\(x_1\)\(>\)\(x_2\),都有\(m[g(x_1)-g(x_2)]\)\(>\)\(x_1f(x_1)\)\(-\)\(x_2f(x_2)\)恒成立,求实数 \(m\) 的取值范围;
解:由题意当 \(x_1>x_2\ge 1\)时,都有 \(m[g(x_1)-g(x_2)]\)\(>\)\(x_1f(x_1)-x_2f(x_2)\) 恒成立,
故当 \(x_1\)\(>\)\(x_2\)\(\ge\)\(1\) 时,\(mg(x_1)\)\(-\)\(x_1f(x_1)\)\(>\)\(mg(x_2)\)\(-\)\(x_2f(x_2)\) 恒成立[同构构造],
此时构造函数 \(H(x)\)\(=\)\(mg(x)\)\(-\)\(xf(x)\),则函数 \(H(x)\) 在区间 \([1,+\infty)\) 上是增函数,则有 \(H'(x)\)\(\ge\)\(0\) 恒成立;
又 \(H(x)\)\(=\)\(m\cfrac{1}{2}x^2\)\(-\)\(xlnx\),则 \(H'(x)\)\(=\)\(mx\)\(-\)\(\ln x\)\(-\)\(1\)\(\ge\)\(0\) 恒成立,
分离参数得到 \(m\)\(\ge\)\(\cfrac{lnx+1}{x}\),再令 \(h(x)\)\(=\)\(\cfrac{lnx+1}{x}\)(\(x\)\(\ge\)\(1\)),
则 \(h'(x)\)\(=\)\(\cfrac{1-lnx-1}{x^2}\)\(=\)\(\cfrac{-lnx}{x^2}\)\(\leq\)\(0\),故 \(h(x)\) 在 \([1,+\infty)\) 上单调递减;
则 \(h(x)_{max}\)\(=\)\(h(1)\)\(=\)\(1\),故有 \(m\) \(\ge\) \(1\)。
(1). 讨论函数\(f(x)\)的单调性。
分析:先求定义域得\((0,+\infty)\),求导得到\(f'(x)\)\(=\)\(\cfrac{a+1}{x}\)\(+\)\(2ax\)\(=\)\(\cfrac{2ax^2+a+1}{x}\),然后只考虑分子函数 \(g(x)\)\(=\)\(2ax^2\)\(+\)\(a\)\(+\)\(1\) 的图像,再考虑 \(a=0\),再考虑函数 \(g(x)\) 图像恒在 \(x\) 轴上方,恒在 \(x\) 轴下方,以及 \(x\) 轴上方下方都有图像的情形,自然就得到了分类的标准有\(a=0\),\(a>0\),\(a+1\leq 0\),以及\(-1<a<0\),解答完做个综述就行了。
解:先求定义域得\((0,+\infty)\),求导得到\(f'(x)\)\(=\)\(\cfrac{a+1}{x}\)\(+\)\(2ax\)\(=\)\(\cfrac{2ax^2+a+1}{x}\),
当\(a\ge 0\)时,\(g(x)>0\)恒成立,则\(f'(x)=\cfrac{2ax^2+a+1}{x}>0\),故\(f(x)\)在\((0,+\infty)\)上单调递增;
当\(a\leq -1\)时,\(g(x)\leq 0\)恒成立,则则\(f'(x)=\cfrac{2ax^2+a+1}{x}<0\),故\(f(x)\)在\((0,+\infty)\)上单调递减;
当\(-1<a<0\)时,令\(f'(x)=0\),解得\(x=\sqrt{-\cfrac{a+1}{2a}}=x_0\),即\(x\in(0,x_0)\)时,\(f'(x)>0\),
故\(f(x)\)在\((0,x_0)\)上单调递增;\(x\in(x_0,+\infty)\)时,\(f'(x)<0\),故\(f(x)\)在\((x_0,+\infty)\)上单调递减;
综上所述,略 .
(2). 设\(a<-1\),若对任意\(x_1,x_2\in(0,+\infty)\),恒有\(|f(x_1)-f(x_2)|\ge 4|x_1-x_2|\),求\(a\)的取值范围。
解: 不妨设\(x_1\leq x_2\),由 (1) 可知,\(a<-1\) 时 \(f(x)\)在 \((0,+\infty)\) 单调递减,
从而对任意 \(x_1,x_2\in(0,+\infty)\),恒有 \(|f(x_1)-f(x_2)|\ge 4|x_1-x_2|\),等价转化为 \(f(x_1)-f(x_2)\ge 4(x_2-x_1)\),
即任意 \(x_1,x_2\in(0,+\infty)\),恒有 \(f(x_1)+4(x_1)\ge f(x_2)+4x_2\),[到此完成同构任务]
令 \(g(x)=f(x)+4x\),则 \(x_1\leq x_2\),有 \(g(x_1)\ge g(x_2)\),
即原命题等价于函数 \(g(x)\) 在 \((0,+\infty)\) 上单调递减,则 \(g'(x)\leq 0\) 在\((0,+\infty)\)上恒成立,
即 \(g'(x)\)\(=\)\(\cfrac{a+1}{x}\)\(+\)\(2ax\)\(+\)\(4\)\(=\)\(\cfrac{2ax^2+4x+a+1}{x}\)\(\leq\)\(0\) 在 \((0,+\infty)\) 上恒成立。接下来的思路就比较多了:
思路1️⃣:分离参数得到,\(a\)\(\leq\)\(\cfrac{-4x-1}{2x^2+1}\)
\(=\)\(\cfrac{(2x-1)^2-4x^2-2}{2x^2+1}\)\(=\)\(\cfrac{(2x-1)^2}{2x^2+1}-2\),
故\(a\)\(\leq\)\(-2\)。
思路2️⃣:只关注导函数\(g'(x)\)的分子,令\(h(x)=2ax^2+4x+a+1\),
则转化为\(h(x)\leq 0\)在\((0,+\infty)\)上恒成立,
分离参数得到,\(a\leq (\cfrac{-4x-1}{2x^2+1})_{min}\),
令\(\phi(x)\)\(=\)\(\cfrac{-4x-1}{2x^2+1}\),
解得\(\phi'(x)\)\(=\)\(\cfrac{-4(2x^2+1)-(-4x-1)\cdot 4x}{(2x^2+1)^2}\)
\(=\)\(\cfrac{8x^2+4x-4}{(2x^2+1)^2}\)\(=\)\(\cfrac{4(2x-1)(x+1)}{(2x^2+1)^2}\),
故\(x\in(0,\cfrac{1}{2})\)时,\(\phi'(x)<0\),\(\phi(x)\)单调递减,
\(x\in(\cfrac{1}{2},+\infty)\)时,\(\phi'(x)>0\),\(\phi(x)\)单调递增,
故\(\phi(x)_{min}=\phi(\cfrac{1}{2})=-2\),故\(a\leq -2\)。
思路3️⃣:只关注导函数\(g'(x)\)的分子,令\(h(x)=2ax^2+4x+a+1\),
则转化为\(h(x)\leq 0\)在\((0,+\infty)\)上恒成立,利用二次函数求解。
则\(\begin{cases}h(0)\leq 0\\x=-\cfrac{4}{2\times 2a}<0\\\Delta >0\end{cases}\)或者\(\Delta \leq 0\),
解得\(a\leq -2或a\ge 1\),又\(a<-1\),故\(a\leq -2\)。
思路4️⃣:接思路1,分离参数得到,\(a\leq \cfrac{-4x-1}{2x^2+1}\),
求函数\(\phi(x)=\cfrac{-4x-1}{2x^2+1}\)的最小值,还可以用代换法,令\(-4x-1=t<-1\),
则\(\phi(x)\)\(=\)\(\cfrac{t}{\cfrac{(t+1)^2}{8}+1}\)\(=\)\(\cfrac{8t}{t^2+2t+9}\)
\(=\)\(\cfrac{8}{t+\cfrac{9}{t}+2}\)\(\ge\)\(\cfrac{8}{-2\sqrt{9}+2}\)\(=\)\(-2\),
故\(a\)\(\leq\)\(-2\)。
此处是利用移项作差来构造新函数,且从简原则,我们不需要构造 \(g(x)\)\(=\)\(f(x)\)\(-\)\(\cfrac{1}{2}x^2\)\(+\)\(C\),相当于直接令 \(C=0\),只强调其存在性,而不是唯一性; ↩︎
本题目中的两次等价变形真的太不容易想到了,但是参照求解过程,我们似乎也能慢慢悟出点道理来,第一次的等价变形 \(f(-x)\)\(-\)\(\cfrac{1}{2}(-x)^2\)\(+\)\(f(x)\)\(-\)\(\cfrac{1}{2}(x)^2\)\(=\)\(0\),是为了得到 \(g(-x)\)\(+\)\(g(x)\)\(=\)\(0\),则函数 \(g(x)\) 为定义在 \(R\) 上的奇函数;第二次的等价变形 \(f(4-m)\)\(-\)\(\cfrac{1}{2}(4-m)^2\)\(\ge\)\(f(m)\)\(-\)\(\cfrac{1}{2}m^2\),是为了满足 \(g(4-m)\) \(\ge\) \(g(m)\) . ↩︎

 尝试总结、提炼导数题目中的构造函数的常用套路,熟悉套路和思路,快速准确解题。
尝试总结、提炼导数题目中的构造函数的常用套路,熟悉套路和思路,快速准确解题。

