恒等变形蕴含的思维层次
前言
我们一般认为 对于表达式 \(f(-x)=-f(x)\) 和 \(f(-x)+f(x)=0\) 是等价的, \(S_{k+2}\)\(+\)\(S_{k+1}\)\(-\)\(2S_{k}=0\) 和 \(S_{k+2}\)\(+\)\(S_{k+1}\)\(=\)\(2S_{k}\) 也是等价的,但是在具体的解题中,我们感觉他们似乎又不是等价的,或者准确的说,不同的表达形式蕴含的思维层次是不一样的。
案例剖析
证法1: 采用 \(S_{k+2}+S_{k+1}=2S_{k}\) 来证明;
由于 \(S_{k+2}=\cfrac{a_1\cdot[1-(-2)^{k+2}]}{1-(-2)}=\cfrac{a_1\cdot[1-(-2)^{k+2}]}{3}\) ,
则 \(S_{k+1}=\cfrac{a_1\cdot[1-(-2)^{k+1}]}{1-(-2)}=\cfrac{a_1\cdot[1-(-2)^{k+1}]}{3}\) ,
则 \(S_{k}=\cfrac{a_1\cdot[1-(-2)^{k}]}{1-(-2)}=\cfrac{a_1\cdot[1-(-2)^{k}]}{3}\) ,
又 \(S_{k+2}+S_{k+1}=\cfrac{a_1\cdot[1-(-2)^{k+2}]}{3}+\cfrac{a_1\cdot[1-(-2)^{k+1}]}{3}\)
\(=\cfrac{a_1[2+2\cdot (-2)^{k+1}-(-2)^{k+1}]}{3}=\cfrac{a_1[2+(-2)^{k+1}]}{3}\)
\(2S_k=\cfrac{2a_1[1-(-2)^k]}{3}=\cfrac{a_1[2-2\cdot (-2)^{k}]}{3}=\cfrac{a_1[2+(-2)^{k+1}]}{3}\)
所以,\(S_{k+2}+S_{k+1}=2S_k\) ,故对任意 \(k\in{N}^{*}\), \(S_{k+2}\), \(S_{k}\), \(S_{k+1}\) 成等差数列.
证法2: 采用 \(S_{k+2}+S_{k+1}-2S_{k}=0\) 来证明;
对任意实数 \(k\in {N}^{*}\), \(S_{k+2}+S_{k+1}-2S_{k}=(S_{k+2}-S_{k})+(S_{k+1}-S_{k})\)
\(=a_{k+1}+a_{k+2}+a_{k+1}=2a_{k+1}+a_{k+1}\cdot(-2)=0\)
所以对任意 \(k\in{N}^{*}\), \(S_{k+2}\), \(S_{k}\), \(S_{k+1}\) 成等差数列.
解后反思:1、对于等差数列的证明方法的依据,我们应该想起的是 ① 定义法:\(a_{n+1}\)\(-\)\(a_n\)\(=\)\(d\),和 ② 等差中项法:\(a_{n+1}\)\(+\)\(a_{n-1}\)\(=\)\(2a_n\);当采用等差中项法证明此题目时,最应该想到的使用方法是等差中项法,从而想到采用 \(S_{k+2}\)\(+\)\(S_{k+1}\)\(=\)\(2S_{k}\) 来证明;这样的话,我们自然会想到采用等比数列的前 \(n\) 项和公式,通过分别计算左右相等的方式证明命题;
2、但是如果采用等差中项法的等价形式:\(S_{k+2}+S_{k+1}-2S_{k}=0\) 来证明,我们可以将左式变形为 \((S_{k+2}\)\(-\)\(S_{k})\)\(+\)\((S_{k+1}\)\(-\)\(S_{k})\),从而可以另辟蹊径,采用 \(a_n\)\(=\)\(S_{n}\)\(-\)\(S_{n-1}\) 更一般化的定义式来确定变形,从而省略了大量的繁杂计算,证明过程简洁明快。
法1:采用验证 \(f(-x)=\pm f(x)\) 的思路变形得到, 变形的难度较大;
\(f(-x)=ln(\sqrt{x^2+1}+x)=ln(\cfrac{1}{\sqrt{x^2+1}-x})\)
\(=ln(\sqrt{x^2+1}-x)^{-1}=-ln(\sqrt{x^2+1}-x)=-f(x)\)
即函数\(f(x)\)为奇函数;
备注:其中用到的公式注解,\((\sqrt{x^2+1}+x)(\sqrt{x^2+1}-x)=1\);
法2:采用定义的等价式验证, \(f(-x)\pm f(x)=0\),变形运算的难度很小;
由于\(f(x)=ln(\sqrt{x^2+1}-x)\),则\(f(-x)=ln(\sqrt{x^2+1}+x)\),
即\(f(x)+f(-x)=ln(\sqrt{x^2+1}-x)+ln(\sqrt{x^2+1}+x)=ln1=0\),即函数\(f(x)\)为奇函数;
分析:同上例,可知\(g(-x)=lg(\sqrt{sin^2x+1}\mp sinx)\),
即\(g(x)+g(-x)=lg1=0\),即函数\(g(x)\)为奇函数;
解后反思:虽然说 \(f(-x)=-f(x)\) 和 \(f(-x)+f(x)=0\) 是等价的,但是有时候我们感觉二者是有区别的,尤其是涉及到对数型函数的奇偶性的判断时,更是如此;很明显,利用 \(f(-x)+f(x)=0\) 变形的同学的思维层次水平要更高一些,能节省较多时间。
思维提升
那么,如何提升我们的思维层次呢?暂时能想到的是:
1、碰到有关恒等变形的表达式,自己有意识的对其作以拓展延伸,用恒等变形的各种不同形式,培养和延伸思维触突,已延展思维链条,活化思维。
实例1,关于数列的变形延申,比如碰到数列中的 \(a_n=n^2+n\),可以考虑将其写为 \(a_n=n^2+n=n(n+1)\),这样若用到 \(\cfrac{1}{a_n}\),自然就能想到 \(\cfrac{1}{a_n}=\cfrac{1}{n(n+1)}=\cfrac{1}{n}-\cfrac{1}{n+1}\),
实例2,关于函数的变形延伸,如\(f(x)=\cfrac{x^2-2x+2}{x-1}\)\(=\)\(\cfrac{(x-1)^2+1}{x-1}\)\(=(x-1)+\cfrac{1}{x-1}\),便于利用模板函数 \(y=x+\cfrac{1}{x}\) 变形得到\(f(x)\);
实例3,关于函数 \(x=\cfrac{1-t}{1+t}=\cfrac{-t-1+2}{1+t}=-1+\cfrac{2}{1+t}\),对于表达式 \(x=\cfrac{1-t}{1+t}\) 我们就不容易看清其单调性,但是当变形为 \(x=-1+\cfrac{2}{1+t}\) 时,做其图像和判定单调性就变得非常容易了。
2、相同的数学公式的不同使用场景和不同使用条件的熟悉和强化,有助于提升思维层次;
实例3、三角形的面积公式的各种使用场景
当涉及直线和圆锥曲线问题求三角形的面积时,常使用 \(S_{\triangle ABC}=\cfrac{1}{2}\times a\times h_a\);
当涉及极坐标求三角形的面积时,常使用 \(S_{\triangle ABC}=\cfrac{1}{2}\times \rho_1\times \rho_2\times sin(\theta_1-\theta_2)\);
当涉及三角函数和解三角形问题求三角形的面积时,常使用 \(S_{\triangle ABC}=\cfrac{1}{2}\times a\times b\times sinC\);
3、简洁清晰的恒等变形的结果带来的便利性会催生我们对思维的提升;
解法一: 方程 \(f(x)=\cfrac{k}{x}\) 可化为 \(x\cdot f(x)=k\),
令 \(g(x)=xf(x)\), 则 \(g(x)=\left\{\begin{array}{l}x^{2}-4x, &x\geqslant 4, \\ -x^{2}+4x, &x<4.\end{array} \quad\right.\)
作出 \(g(x)\) 的图象,如图所示, 方程 \(xf(x)=k\) 有三个互不相等的实根 \(x_{1}, x_{2}, x_{3}\),
等价于函数 \(g(x)\) 的图象与直线 \(y=k\) 有三个不同的交点,
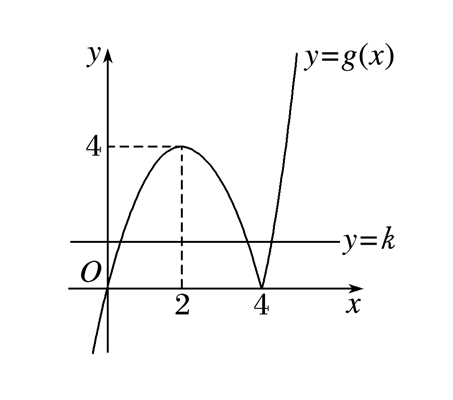
结合图象可知 \(0<k<4\), 不妨设 \(x_{1}<x_{2}<x_{3}\), 由图象可知 \(x_{3}>4\),
由二次函数 \(y=-x^{2}+4 x\)的图象关于直线 \(x=2\) 对称可知,\(\cfrac{x_{1}+x_{2}}{2}=2\),
即 \(x_{1}+x_{2}=4\),令 \(x^{2}-4x=4\), 解得 \(x=2\pm 2\sqrt{2}\), 所以 \(4<x_{3}<2+2\sqrt{2}\),
所以 \(4+4<x_{1}+x_{2}+x_{3}<4+2+2\sqrt{2}\),即 \(8<x_{1}+x_{2}+x_{3}<6+2\sqrt{2}\),. 故选 \(D\).
解法二:直接利用题目给定的条件,拆分为函数 \(y=f(x)\) 和函数 \(y=\cfrac{k}{x}\)有三个不同的交点,如下图所示,
由图可知, 函数 \(y=\cfrac{k}{x}\) 与 函数 \(y=-x+4(x<4)\) 应该有两个交点\(x_1\),\(x_2\)(不妨令 \(x_1<x_2\) ),函数 \(y=\cfrac{k}{x}\) 与 函数 \(y=x-4(x\geqslant 4)\) 应该有一个交点\(x_3\)( \(x_3>4\) ),
由 \(f(x)=\left\{\begin{array}{l}y=-x+4,&x\geqslant 4\\y=\cfrac{k}{x},&x>0,k>0\end{array}\right.\) 可得到,
\(x^2-4x+k=0\),则由韦达定理可知 \(x_1+x_2=4\),
且由 \(x^2-4x+k=0\)可知, 当 \(k=4\)时,\(y=-x+4(x<4)\)和 \(y=\cfrac{k}{x}\) 相切,
当\(k>4\)时,\(y=-x+4(x<4)\)和 \(y=\cfrac{k}{x}\) 相离,不满足有三个交点的情形,
当\(0<k<4\)时, \(y=-x+4(x<4)\)和 \(y=\cfrac{k}{x}\) 有两个交点,\(y=x-4(x\geqslant 4)\)和 \(y=\cfrac{k}{x}\) 有一个交点,满足题意;
在此动态变化过程中,可以看出 \(x_3\) 的范围的下限为 \(4\),其上限的求解,需要 \(k=4\),
从而联立 \(y=\cfrac{k}{x}\) 和 \(y=x-4(x\geqslant4)\) 求解得到 \(x_3=2+2\sqrt{2}\)(舍去 \(x_3=2-2\sqrt{2}\) ),
故得到 \(4<x_3<2+2\sqrt{2}\),
所以 \(4+4<x_{1}+x_{2}+x_{3}<4+2+2\sqrt{2}\),即 \(8<x_{1}+x_{2}+x_{3}<6+2\sqrt{2}\),. 故选 \(D\).
解后反思:在由数转化为形的过程中,我们有两个变形的思路:其一,[首先想到,也最容易想到的]直接利用题目给定的条件,拆分为函数 \(y=f(x)\) 和函数 \(y=\cfrac{k}{x}\)有三个不同的交点;其二,先转化为方程 \(xf(x)=k\) 有三个互不相等的实根 \(x_{1}, x_{2}, x_{3}\),再转化为利用形来求解,相比而言,明显此思路要更先进一些,思维的层次就更高一些,作图也便利,还能利用函数的对称性。
4、各种常见常用的数学式之间的恒等变形需要我们有意识的记忆、积累,以便于转化划归,比如根式,分式,换元法,对勾函数等等常用素材的融合使用。
\(=\cfrac{1}{2}\cdot 1\cdot\sqrt{(y_{1}+y_{2})^{2}-4y_{1}y_{2}}\)
\(=\cfrac{1}{2} \sqrt{\cfrac{4m^{2}}{(2+m^{2})^{2}}+\cfrac{4}{2+m^{2}}}\)
\(=\cfrac{\sqrt{2}\sqrt{1+m^{2}}}{2+m^{2}}\)
\(=\cfrac{\sqrt{2}}{\sqrt{1+m^{2}}+\cfrac{1}{\sqrt{1+m^{2}}}}\),
设 \(t=\sqrt{1+m^{2}}\geqslant 1\), 则 \(y=t+\cfrac{1}{t}\) 在 \(t\in[1,+\infty)\) 单调递增,
所以 \(t=1\) 时, 此时即 \(m=0\) 时, \(y=2\) 最小,
即当 \(m=0\)时, \((S_{\triangle AOB})_\max =\cfrac{\sqrt{2}}{2}\).
5、灵活巧妙的利用恒等变形,可以拓展我们的思维,延申思维的触角,让我们的思维走的更远
证明:当 \(a=1\) 时, 函数 \(f(x)=e^x-lnx-\cfrac{m^2}{2} (x>0)\), 则 \(f'(x)={e}^{x}-\cfrac{1}{x}\),
令 \(g(x)={e}^{x}-\cfrac{1}{x}\),则 \(g'(x)=e^x+\cfrac{1}{x^2}\),
因为 \(g'(x)>0\),所以函数 \(g(x)\) 在 \((0,+\infty)\) 上单调递增,
又因为 \(g(\cfrac{1}{2})=\sqrt{e}-2<0\),\(g(1)={e}-1>0\),
所以存在 \(x_{0}\in(\cfrac{1}{2}, 1)\),使 \({e}^{x_0}=\cfrac{1}{x_{0}}\), 可得 \(x_{0}=-\ln x_{0}\)这一步变换是非常关键的一步,在下面求最值时,需要用到这些变换,以简化求最值时的函数的形式。比如后边将函数 \({e}^{x_0}-\ln x_{0}\)等价转化为 容易求最值的函数\(\cfrac{1}{x_{0}}+x_{0}\),
所以对任意 \(x\in(0,x_{0})\),\(g(x)<0\), 即 \(f'(x)<0\),
函数 \(f(x)\) 在 \((0,x_0)\) 上单调递减,
对任意 \(x\in(x_{0},+\infty)\), \(g(x)>0\), 即 \(f'(x)>0\),
函数 \(f(x)\) 在 \((x_0,+\infty)\) 上单调递增,
所以 \(f(x)_{\min}=f(x_{0})={e}^{x_{0}}-\ln x_{0}-\cfrac{m^{2}}{2}\),
要证明函数 \(f(x)\) 的图像均在 \(x\) 轴上方,只需证明 \(f(x)_{\min}>0\),
即当 \(x_0\in (\cfrac{1}{2},1)\) 时,\({e}^{x_{0}}-\ln x_{0}-\cfrac{m^{2}}{2}>0\) 恒成立,
即 \(\cfrac{m^{2}}{2}<{e}^{x_0}-\ln x_{0}=\cfrac{1}{x_{0}}+x_{0}\) 在 \(x_{0}\in(\cfrac{1}{2}, 1)\) 上恒成立,
因为当 \(x_{0}\in(\cfrac{1}{2}, 1)\) 时,函数 \(u(x_0)=\cfrac{1}{x_0}+x_0\) 是减函数,
所以 \(2<\cfrac{1}{x_{0}}+x_{0}<\cfrac{5}{2}\),
即 \(\cfrac{m^2}{2}\leqslant 2\) ,解得 \(-2\leqslant m\leqslant 2\),
所以,当 \(a=1\) 时,对任意 \(m\in [-2,2]\) ,函数 \(f(x)\) 的图像均在 \(x\) 轴上方.
6、积累常用的恒等变形式,透彻理解变形的目的,有助于提升我们的数学思维;
\(e^{x+1}\)\(\cdot\)\(f(2x-1)\)\(-\)\(f(x-2)\)\(>0\)
\(\Leftrightarrow\) \(\cfrac{e^{2x-1}}{e^{x-2}}f(2x-1)-f(x-2)>0\)
\(\Leftrightarrow\) \(e^{2x-1}\cdot f(2x-1)>e^{x-2}\cdot f(x-2)\),
辅助说明:\(e^{x+1}=e^{(2x-1)-(x-2)}=\cfrac{e^{2x-1}}{e^{x-2}}\)
典例剖析
【法1】:如图所示,由\((b+2c)cosA=-acosB\),边化角,得到\(A=120^{\circ}\),
设\(BD=CD=y\),\(AB=x\),\(\angle ADB=\alpha\),\(\angle ADC=\beta\),

在\(\triangle ABC\)中,\(AB=x\),\(AC=4\),\(BC=2y\),\(A=120^{\circ}\),
则由余弦定理得到\((2y)^2=x^2+16-2\cdot 4x\cdot cos120^{\circ}\)①,
又在\(\triangle ADB\)和\(\triangle ADC\)中,由\(cos\alpha+cos\beta=0\),得到\(\cfrac{7+y^2-x^2}{2\sqrt{7}y}+\cfrac{7+y^2-16}{2\sqrt{7}y}=0\)②,
联立①②,得到\(x=6\)或\(x=-2\)(舍去),故选\(A\)。
【法2】:由\((b+2c)cosA=-acosB\),边化角,得到\(A=120^{\circ}\),
由于点\(D\)为\(BC\)的中点,利用向量方法,
\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}\),两边平方,得到
\(|\overrightarrow{AB}|^2+|\overrightarrow{AC}|^2+2\overrightarrow{AB}\cdot \overrightarrow{AC}cos120^{\circ}=4|\overrightarrow{AD}|^2\),
即\(x^2+16+2\cdot x\cdot 4\cdot (-\cfrac{1}{2})=28\),
化简为\(x^2-4x-12=0\),解得\(x=6\)或\(x=-2\)(舍去),故选\(A\)。
【解后反思】:法1为通法,运算难度较大,法2为特殊解法,运算简洁,但是如果点\(D\)变化为四分之三等分点,法2就失效了;同时注意,出现 \(\overrightarrow{AB}\)\(+\)\(\overrightarrow{AC}\)\(=\)\(2\overrightarrow{AD}\) 或者 \(\overrightarrow{AD}\)\(=\)\(\cfrac{1}{2}\)\((\overrightarrow{AB}\)\(+\)\(\overrightarrow{AC})\) ,意味着点 \(D\) 为 \(BC\) 的中点。
思路一: \(f(x)=\sqrt{3}\cos2x-2\cos x\sin x=\sqrt{3}\cos2x-\sin2x=2\cos(2x+\cfrac{\pi}{6})\),
令 \(2x+\cfrac{\pi}{6}=k\pi\),(\(k\in Z\)),解得对称轴方程 为 \(x=\cfrac{k\pi}{2}-\cfrac{\pi}{12}\),(\(k\in Z\)),
思路二: \(f(x)=\sqrt{3}\cos2x-2\cos x\sin x=\sqrt{3}\cos2x-\sin2x=-2\sin(2x-\cfrac{\pi}{3})\),
令 \(2x-\cfrac{\pi}{3}=k\pi+\cfrac{\pi}{2}\),(\(k\in Z\)),解得对称轴方程 为 \(x=\cfrac{k\pi}{2}+\cfrac{5\pi}{12}\),(\(k\in Z\)),
问题:这两个对称轴方程一样吗?为什么?
二者是一样的, 在 \(x=\cfrac{k\pi}{2}+\cfrac{5\pi}{12}\) ,(\(k\in Z\))中,
令 \(k=n-1\),则 \(x=\cfrac{(n-1)\pi}{2}+\cfrac{5\pi}{12}=\cfrac{n\pi}{2}-\cfrac{\pi}{12}\),(\(n\in Z\)),
再换参数表达,也即 \(x=\cfrac{k\pi}{2}-\cfrac{\pi}{12}\),(\(k\in Z\)),故是一样的,
另外针对的是同一个函数所作的恒等变形,故结果一定应该是一样的。
- 由指数的运算法则我们知道,\((a^m)^n=(a^n)^m=a^{mn}\),那么 \(e^{2x}=(e^2)^x=(e^x)^2\),
那么函数 \(y=e^{2x}\) 既可以拆分为 \(y={(e^2)}^x\) ,也可以拆分为 \(y=(e^x)^2\) ,但是拆分为 \(y={(e^2)}^x\) 的思维层次就要高一些,因为函数 \(y={(e^2)}^x\) 是指数函数,属于基本初等函数,其图像非常好想好做,而 \(y=(e^x)^2\) 是个复合函数,是指数函数的平方,我们不太好想其中的细节。

 虽说采用的都是恒等变形,但是不一样的变形方向体现了不一样的思维层次,也对应着不同的结果。
虽说采用的都是恒等变形,但是不一样的变形方向体现了不一样的思维层次,也对应着不同的结果。
