定比分点坐标公式
定比分点坐标公式，在高考中考查的不是很多，不过对其整理，便于理解与其关联的其他知识点。
前言
定比分点坐标公式，在高考中考查的不是很多，不过对其整理，便于理解与其关联的其他知识点。
平面几何推导思路
在平面直角坐标系中，已知两点 \(A(x_1，y_1)\)，\(B(x_2，y_2)\)，过两点的直线上有一点 \(P\)，设其坐标为\(P(x，y)\)，
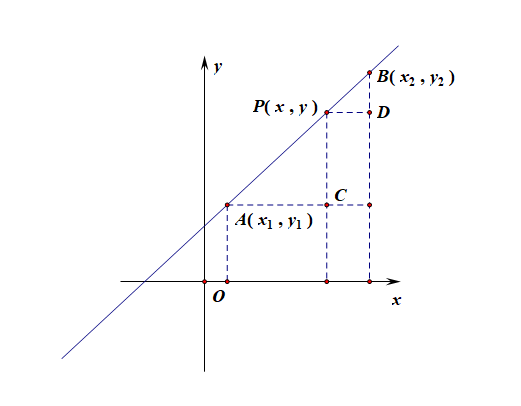
分别过点 \(A\)， \(P\)， \(B\)作坐标轴的垂线，可得交点 \(C(x，y_1)\)， \(D(x_2，y)\)，
由图可知， \(\triangle ACP\sim \triangle PDB\)，则有 \(\cfrac{AC}{PD}=\cfrac{PC}{BD}\)，[\(\cfrac{AC}{PD}=\cfrac{AP}{PB}\)]
即 \(\cfrac{x-x_1}{x_2-x}=\cfrac{y-y_1}{y_2-y}\)，
设此比值为\(\lambda\) ，则 \(\overrightarrow{AP}:\overrightarrow{PB}=\lambda\)，
则由\(\cfrac{x-x_1}{x_2-x}=\cfrac{y-y_1}{y_2-y}=\lambda\)，可以解得，
那么我们说点 \(P\) 分有向线段 \(\overrightarrow{AB}\) 的比为\(\lambda\)，称点 \(P\) 为定比分点，并将上式称为定比分点坐标公式。
当 \(P\) 为内分点时， \(\lambda>0\) ；当 \(P\) 为外分点时， \(\lambda<0(\lambda\neq -1)\) ；当 \(P\) 与 \(A\) 重合时， \(\lambda=0\) ；当 \(P\) 与 \(B\) 重合时， \(\lambda\) 不存在。
向量推导思路
如图，已知线段\(P_1P_2\)的端点 \(P_1(x_1,y_1)\)、\(P_2(x_2,y_2)\)，点 \(P(x,y)\) 为直线 \(P_1P_2\) 上的一点，当 \(\overrightarrow{P_1P}=\lambda\overrightarrow{PP_2}\) 时，求证：
证明：由题可知，\(\overrightarrow{P_1P}=(x-x_1,y-y_1)\)，\(\overrightarrow{PP_2}=(x_2-x,y_2-y)\)，
由于 \(\overrightarrow{P_1P}=\lambda\overrightarrow{PP_2}\) ，即 \((x-x_1,y-y_1)=\lambda(x_2-x,y_2-y)\)，
则有 \(x-x_1=\lambda(x_2-x)\)，\(y-y_1=\lambda(y_2-y)\)，
解得，\(x=\cfrac{x_1+\lambda x_2}{1+\lambda}\) ， \(y=\cfrac{y_1+\lambda y_2}{1+\lambda}\) . 证毕
公式应用
【重要结论】线段的中点坐标公式 \(P_1(x_1,y_1)\)、\(P_2(x_2,y_2)\)，点 \(P(x,y)\) 为线段的中点，则 \(x=\cfrac{x_1+x_2}{2} ， y=\cfrac{y_1+y_2}{2}\)
证明思路1：当点 \(P\) 为线段 \(AB\) 的中点时，则 \(\lambda=1\) ，代入定比分点公式可得中点坐标公式：
证明思路2：在平面直角坐标系中，设与 \(x\) 轴，\(y\) 轴方向相同的两个单位向量分别为 \(\vec{i}\)，\(\vec{j}\)，取 \(\{\)\(\vec{i}\),\(\vec{j}\)\(\}\) 作为基底，
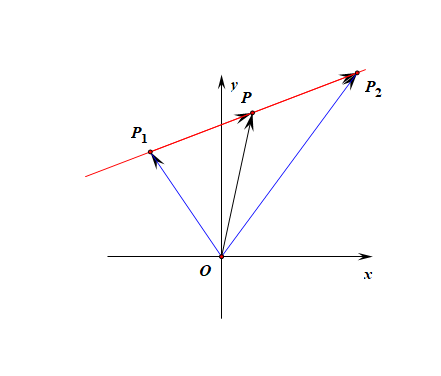
则可知 \(\overrightarrow{OP_1}=(x_1,y_1)\)，\(\overrightarrow{OP_2}=(x_2,y_2)\)，由向量的线性运算可知，
\(\overrightarrow{OP}=\cfrac{1}{2}(\overrightarrow{OP_1}+\overrightarrow{OP_2})=(\cfrac{x_1+x_2}{2},\cfrac{y_1+y_2}{2})\)，
所以，点 \(P\) 的坐标是 \((\cfrac{x_1+x_2}{2},\cfrac{y_1+y_2}{2})\) .
【重要结论】三角形重心坐标公式：若三角形的三个顶点坐标分别为\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，\(C(x_3，y_3)\)，则其重心 \(M(x_0，y_0)\) 满足 \(x_0=\cfrac{x_1+x_2+x_3}{3}\)，\(y_0=\cfrac{y_1+y_2+y_3}{3}\)，
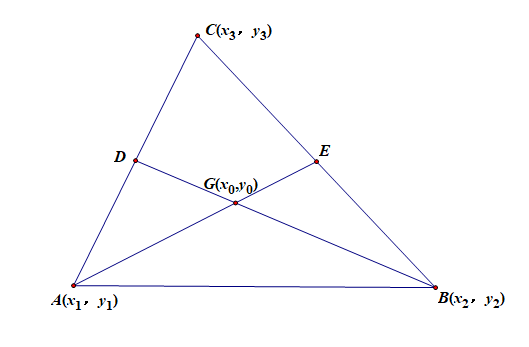
证法1：【几何方法】如图所示，重心\(G\)在以\(BC\)为底边的中线\(AE\)上，则点\(E\)的横坐标\(x_E=\cfrac{1}{2}(x_2+x_3)\)，点\(E\)的纵坐标\(y_E=\cfrac{1}{2}(y_2+y_3)\)，且有\(EG=\cfrac{1}{2}AG\)，\(EG=\cfrac{1}{3}AE\)，
为使用定比分点坐标公式，梳理如下：
已知线段\(AE\)，且有\(A(x_1，y_1)\)，\(E(\cfrac{x_2+x_3}{2}，\cfrac{y_2+y_3}{2})\)，定比为\(\lambda=\cfrac{AG}{GE}=2\)，
则定比分点\(G\)即三角形的重心\(G(x_0，y_0)\)的坐标为：
\(x_0=\cfrac{x_1+\lambda x_E}{1+\lambda}=\cfrac{x_1+2\times \cfrac{x_2+x_3}{2}}{1+2}=\cfrac{x_1+x_2+x_3}{3}\)，
\(y_0=\cfrac{y_1+\lambda y_E}{1+\lambda}=\cfrac{y_1+2\times \cfrac{y_2+y_3}{2}}{1+2}=\cfrac{y_1+y_2+y_3}{3}\)；证毕。
证法2：【向量方法】首先由中点坐标公式可知，\(E(\cfrac{x_2+x_3}{2},\cfrac{y_2+y_3}{2})\)，又 \(\overrightarrow{AG}=\cfrac{2}{3}\overrightarrow{AE}\)
即 \((x_0-x_1,y_0-y_1)=\cfrac{2}{3}(\cfrac{x_2+x_3}{2}-x_1,\cfrac{y_2+y_3}{2}-y_1)\)，
则有 \(x_0-x_1=\cfrac{2}{3}(\cfrac{x_2+x_3}{2}-x_1)\)，\(y_0-y_1=\cfrac{2}{3}(\cfrac{y_2+y_3}{2}-y_1)\)，
整理即得到，\(x_0=\cfrac{x_1+x_2+x_3}{3}\)，\(y_0=\cfrac{y_1+y_2+y_3}{3}\)；证毕。
典例剖析
解析：在平面直角坐标系中，已知两点 \(A(x_1，y_1)\)，\(B(x_2，y_2)\)，在直线上任取一点 \(P\)，设其坐标为\(P(x，y)\)，
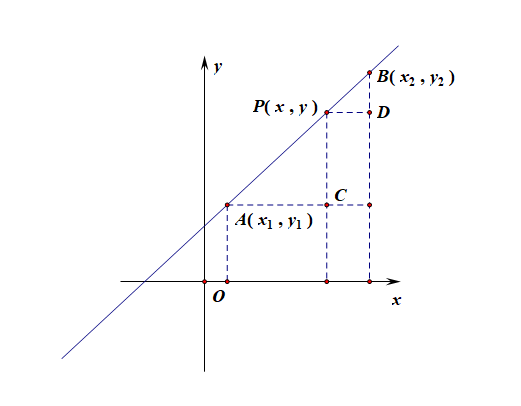
分别过点 \(A\)， \(P\)， \(B\)作坐标轴的垂线，可得交点 \(C(x，y_1)\)， \(D(x_2，y)\)，
由图可知， \(\triangle ACP\sim \triangle PDB\)，则有 \(\cfrac{AC}{PD}=\cfrac{PC}{BD}\)，[\(\cfrac{AC}{PD}=\cfrac{AP}{PB}\)]
即 \(\cfrac{x-x_1}{x_2-x}=\cfrac{y-y_1}{y_2-y}\)，
设此比值为\(\lambda\) ，则 \(\overrightarrow{AP}:\overrightarrow{PB}=\lambda\)，
则由\(\cfrac{x-x_1}{x_2-x}=\cfrac{y-y_1}{y_2-y}=\lambda\)，可以解得，
这就是经过两点 \(A(x_1，y_1)\)，\(B(x_2，y_2)\) 的直线的参数方程，其中参数 \(\lambda\) 的几何意义是点 \(P\) 分有向线段 \(\overrightarrow{AB}\) 的数量比 \(\cfrac{AP}{PB}\).
备注：这种形式的直线的参数方程在教材上出现的用意，是为了让学生体会采用不同的参数，同样的直线可以有不同的参数方程的外在形式，高考中不做考查。
