高次方程解法+高次代数式分解

前言

高次方程在高中阶段，也就是在求解过点处的切线、穿根法求解不等式、等比数列中碰到过，不是很多。高次代数式可能出现在导数判断单调性中。

定义方法

高次方程指次数等于或者大于 \(3\) 次的方程，高中学生主要求解的方程的次数大多是 \(2\) 次的方程，所以对高次方程的求解比较陌生。

与求解高次方程有关的方法主要有：试商法、多项式除法、分组分解法、十字相乘法、换元法等；

切线方程

求曲线\(C:y=\cfrac{1}{3}x^3+\cfrac{4}{3}\)经过点\(P(2，4)\)的切线方程；（\(4x-y-4=0\)或\(x-y+2=0\)）

思路：设经过点\(P(2，4)\)的切线方程与曲线相切于点\(P_0(x_0，y_0)\)，则有

\(\begin{cases}y_0=\cfrac{1}{3}x_0^3+\cfrac{4}{3}\\ k=f'(x_0)=x_0^2\\ y-y_0=f'(x_0)(x-x_0) \end{cases}\)

又因为点\(P(2，4)\)在切线方程上，则有\(4-(\cfrac{1}{3}x_0^3+\cfrac{4}{3})=x_0^2(2-x_0)\)

整理得到，\(x_0^3-3x_0^2+4=0\)警示，此处有多个难点：试商法，多项式除法，分组分解法；

【试商法】：(也不知这个名称是否合适)令\(x_0=0\)，如果上述方程成立，说明方程能分解出因子\(x_0\)，本题目中显然不成立；再令\(x_0=1\),上述方程不成立，说明方程不能分解出因子\(x_0-1\)；再令\(x_0=-1\),上述方程成立，说明方程能分解出因子\(x_0+1\)；这样\(x_0^3-3x_0^2+4\)\(=(x_0+1)\)\((x_0^2+bx_0+c)\)(\(b\)，\(c\)是常数，待定)，这样做的目的是为了降次；

• 20240408补充，高等代数中有一个定理，叫有理根定理，专门解释上述的做法的理由。

【分组分解法】：由试商法可以指导我们的分组分解的方向，

如\(x_0^3-3x_0^2+4=(x_0^3+1)-3(x_0^2-1)\)

\(=(x_0+1)(x_0^2-x_0+1)-3(x_0+1)(x_0-1)\)

\(=(x_0+1)(x_0^2-x_0+1-3x_0+3)\)

\(=(x_0+1)(x_0-2)^2=0\)；

【多项式除法】：如图所示，

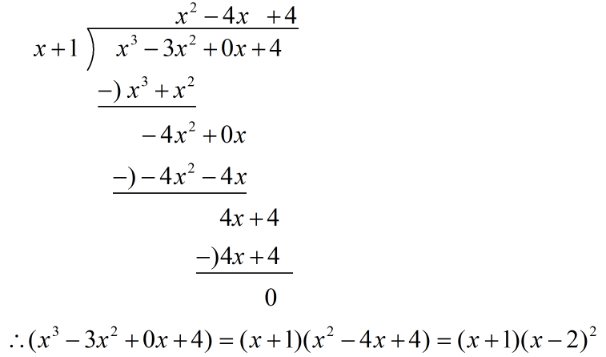
即\((x_0+1)(x_0-2)^2=0\)，解得\(x_0=-1\)，或\(x_0=2\)

当\(x_0=-1\)时，切点为\((-1，1)\)，\(k_1=1\)，切线方程为\(x-y+2=0\)；

当\(x_0=2\)时，切点为\((2，4)\)，\(k_2=4\)，切线方程为\(4x-y-4=0\)；

等比数列

【2021届高三文科资料用题】设数列 \(\{a_{n}\}\) 是等比数列， 前 \(n\) 项和为 \(S_{n}\)， 若 \(S_{3}=3a_{3}\)， 则公比 \(q\)=______________.

法1： 分类讨论法，针对 \(q\) 分类讨论如下：

当 \(q\neq 1\) 时， 由题意得到， \(\cfrac{a_{1}(1-q^{3})}{1-q}=3a_{1}q^{2}\)，

即 \(1-q^{3}=3q^{2}-3q^{3}\)，整理得 \(2q^{3}-3q^{2}+1=0\)，

[备注：接下来可以使用试商法，得到\(q=1\)为其一个根，另外还可以使用多项式除法求解剩余的因式，此处我们往往可以降低难度，使用初中的因式分解法]

则\(2q^{3}-2-3q^{2}+3=0\)，即\(2(q^{3}-1)-3(q^{2}-1)=0\)，则\(2(q-1)(q^2+q+1)-3(q-1)(q+1)=0\)，

即\((q-1)(2q^2-q-1)=0\)，即\((q-1)^2(2q+1)=0\)，

解得 \(q=-\cfrac{1}{2}\)，或 \(q=1\)(舍去)；

当 \(q=1\) 时，即 \(S_{3}=3a_1=3a_{3}\)，显然成立.

故 \(q=-\cfrac{1}{2}\) 或 \(1\)；

法2：使用求和的定义式求解，有效避免分类讨论；

由于 \(S_{3}=3a_{3}\)，即 \(a_1+a_2+a_3=3a_3\)，即 \(a_1+a_2-2a_3=0\)，

由于数列 \(\{a_n\}\) 为等比数列，故 \(a_1+a_1q-2a_1q^2=0\)，

即\(2q^2-q-1=0\)， 解得 \(q=-\cfrac{1}{2}\) 或 \(1\)；

三角函数

计算: \(sin18^{\circ}=\cfrac{\sqrt{5}-1}{4}\)

分析： 由于\(sin3\theta=3sin\theta cos^2\theta-sin^3\theta\)，\(cos2\theta=cos^2\theta-sin^2\theta\)，

又由于\(\sin54^{\circ}=\cos36^{\circ}\)，且\(\sin54^{\circ}=\sin(3\times 18^{\circ})\)，\(\cos36^{\circ}=\cos(2\times18^{\circ})\)，

可得\(3sin18^{\circ}cos^218^{\circ}-sin^318^{\circ}=cos^218^{\circ}-sin^218^{\circ}\).

整理得到，\(4sin^318^{\circ}-2sin^218^{\circ}-3sin18^{\circ}+1=0\)，

用试商法尝试分解\(x=1\)为其一个根，

故可以分解为\((sin18^{\circ}-1)(4sin^218^{\circ}+2sin18^{\circ}-1)=0\)，

\(sin18^{\circ}=1\)舍去，由\(4sin^218^{\circ}+2sin18^{\circ}-1=0\)，

得到\(sin18^{\circ}=\cfrac{-2\pm \sqrt{4+4\times4}}{2\times 4}=\cfrac{-1\pm \sqrt{5}}{4}\)，

舍去负值，得到\(sin18^{\circ}=\cfrac{\sqrt{5}-1}{4}\)，

即\(2sin18^{\circ}=\cfrac{\sqrt{5}-1}{2}\)。

【因式分解案例】令 \(g(x)=\cfrac{e^x-\frac{1}{2}x^3-x-1}{x^2}\)，求导并加以整理变形；

解析： \(g'(x)=\cfrac{(e^x-\frac{1}{2}x^3-x-1)'\cdot x^2-(e^x-\frac{1}{2}x^3-x-1)\cdot 2x}{(x^2)^2}\)

\(=\cfrac{(e^x-\frac{3}{2}x^2-1)\cdot x^2-(e^x-\frac{1}{2}x^3-x-1)\cdot 2x}{x^4}\)

\(=\cfrac{(e^x-\frac{3}{2}x^2-1)\cdot x-(e^x-\frac{1}{2}x^3-x-1)\cdot 2}{x^3}\)

\(=\cfrac{xe^x-\frac{3}{2}x^3-x-2e^x+x^3+2x+2}{x^3}\)

\(=\cfrac{(x-2)e^x-\frac{1}{2}x^3+x+2}{x^3}\)

到此，我们的思维大多就停滞了，难点在分子的三次多项式 \(-\cfrac{1}{2}x^3+x+2\) 的分解上，

此时，用试商法得到，\(x=2\)为其一个根，故分组分解如下，

\(-\cfrac{1}{2}x^3+x+2=-\cfrac{1}{2}x^3+4+x-2\)

\(=-\cfrac{1}{2}(x^3-2^3)+(x-2)=-\cfrac{1}{2}(x-2)(x^2+2x+4)+(x-2)\)

\(=(x-2)(-\cfrac{1}{2}x^2-x-1)\)，

故接上得到，

\(g'(x)=\cfrac{(x-2)e^x-\frac{1}{2}x^3+x+2}{x^3}=\cfrac{(x-2)(e^x-\cfrac{1}{2}x^2-x-1)}{x^3}\)

求解 \(4\cos^4\theta-17\cos^2\theta+4=0\)

解析： 将方程变形为 \((4\cos^2\theta-1)(\cos^2\theta-4)=0\)，

则 \(\cos^2\theta=\cfrac{1}{4}\) 或 \(\cos^2\theta=4\) (舍去)，

则 \(\cos\theta=\pm\cfrac{1}{2}\) 。

【2022届高三数学题目改编】求解方程 \(\cfrac{1}{3}x^3+x^2-\cfrac{2}{3}=0\) .

提示：用试商法尝试， \(x=-1\) 是其一个根，故将上述方程变形如下：

\(\cfrac{1}{3}x^3+\cfrac{1}{3}+x^2-\cfrac{2}{3}-\cfrac{1}{3}=0\) ，即 \(\cfrac{1}{3}(x^3+1)+(x^2-1)=0\)，

即 \(\cfrac{1}{3}(x+1)(x^2-x+1)+(x-1)(x+1)=0\)，为便于计算，将系数整数化，两边同时乘以 \(3\) ，

化简整理得到， \((x+1)(x^2+2x-2)=0\)，解得 \(x=-1\) 或 \(x=-\sqrt{3}-1\) 或 \(x=\sqrt{3}-1\) 。

【2022届高三数学题目改编】因式分解 \(2t^3-t^2-1\) .

分析：就本题目而言，先用试商法判断确定其中的一个因式，以降低其总的次数，便于我们进一步操作。

令 \(t=0\) ， 则 \(2t^3-t^2-1\neq0\) ，说明此三次三项式中不包含因式 \(t\) 或者 \((t-0)\)， 再尝试 \(t=1\)，发现 \(2t^3-t^2-1=0\) ，说明此三次三项式中一定包含因式 \((t-1)\)，那么剩下的因式为什么呢，此时可以考虑两个思路：其一用多项式除法[此法的详细使用参见本博文的相关例子]，其二用分组分解法；

\( \begin{align*} 2t^3-t^2-1 &=2t^3-t^2-2+1\\ &=2t^3-2-t^2+1\\ &=2(t^3-1^3)-(t^2-1^2)\\ &=2(t-1)(t^2+t+1)-(t-1)(t+1)\\ &=(t-1)[2(t^2+t+1)-(t+1)]\\ &=(t-1)(2t^2+t+1)\\ \end{align*} \tag{01} \)

故 \(2t^3-t^2-1=(t-1)(2t^2+t+1)\) 。