在线|十二月解答

需要补充

分式之殇更多与分式有关的内容，请博友在静雅斋数学中自行搜索，；与圆锥曲线有关的定值问题和定点问题；

典例剖析

【北京人大附中高二11月月考第23题改编】已知三棱锥 \(P-ABC\) 的底面 \(ABC\) 为正三角形，点 \(A\) 在侧面 \(PBC\) 上的射影 \(H\) 是 \(\triangle PBC\) 的垂心(三角形的垂心是三角形三条高线的交点)， 延长 \(PH\) 交 \(BC\) 于 \(D\)， 过 \(P\) 作 \(PO\)\(\perp\)\(AD\) 于 \(O\)，延长 \(CO\) 交 \(AB\) 于 \(F\)， 二面角 \(H-AB-C\) 为 \(\cfrac{\pi}{6}\)， 且 \(PA=2\)， 则下列结论成立的有：

①\(BC\perp AD\)；

②二面角 \(P-AB-C\) 的平面角为 \(\angle PBC\)；

③直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\)；

④两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\)；

⑤直线 \(FD\) 与直线 \(PC\) 所成角的余弦值为 \(\cfrac{\sqrt{3}}{3}\)；

⑥三棱锥 \(P-ABC\) 的体积为 \(\cfrac{3}{4}\)；

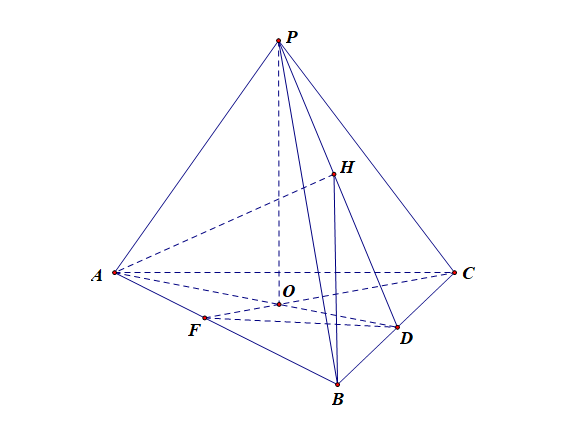
解析：本题目的信息量有点太大，具体解析如下，

①\(BC\perp AD\)；

分析：由于点 \(A\) 在侧面 \(PBC\) 上的射影为 \(H\)，故\(AH\perp\)平面\(PBC\)，由于\(BC\subsetneqq PBC\)，故\(AH\perp BC\)；

又由于\(H\) 是 \(\triangle PBC\) 的垂心，故\(PD\perp BC\)，

由\(BC\perp AH\)，\(BC\perp PD\)，且又\(AH\)，\(PD\subsetneqq\) \(PAD\)、\(AH\cap PD=H\)，

则\(BC\perp\)平面\(PAD\)，又\(AD\subsetneqq\) \(PAD\)，则得到\(BC\perp AD\)；故①成立；

②二面角 \(P-AB-C\) 的平面角为 \(\angle PBC\)；

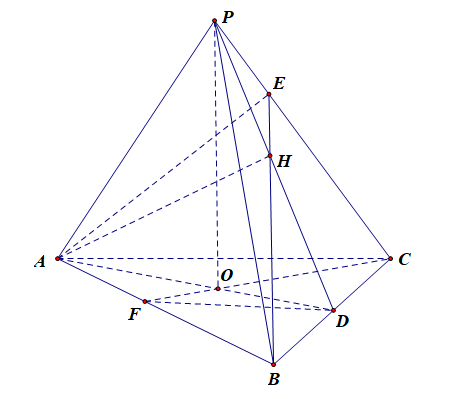
分析：如图所示，延长\(BH\)交\(PC\)于点\(E\)，连结\(AE\)，

则由\(AH\perp PC\)，\(BE\perp PC\)（垂足），\(AH\cap BE=H\)，\(AH\)、\(BE\subsetneqq\) \(ABE\)，

故\(PC\perp\)面\(ABE\)，\(AB\subsetneqq\)面\(ABE\)，

则有\(PC\perp AB\)，又\(PO\perp AB\)，\(PC\cap PO=P\)，\(PC\)、\(PO\subsetneqq\) \(POC\)，

则\(AB\perp\)面\(POC\)，\(CO\subsetneqq\)面\(POC\)，

则得到\(AB\perp CO\)，则\(AB\perp CF\)，

故\(O\)为\(\triangle ABC\)的垂心，又由于三角形为正三角形，

故\(O\)是\(\triangle ABC\)的中心，

故\(P-ABC\)为正三棱锥。

故可知，点\(D\)，\(F\)分别为中点，连结\(PF\)，则可得到\(PF\perp AB\)，

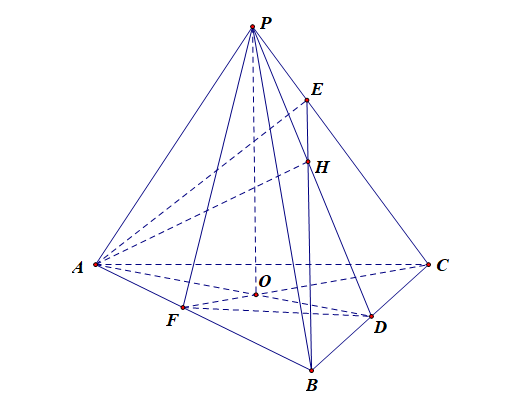
则\(\angle PFC\)为二面角 \(P-AB-C\) 的平面角。故②错误；

③直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\)；

分析：连结\(EF\)，由①②可知，\(AB\perp\)平面\(PCF\)，故\(AB\perp EF\)，又\(PC\perp\)平面\(ABE\)，故\(PC\perp EF\)，

故线段\(EF\)为两条异面直线\(AB\)和\(PC\)的公垂线，又由于\(CF\perp AB\)，

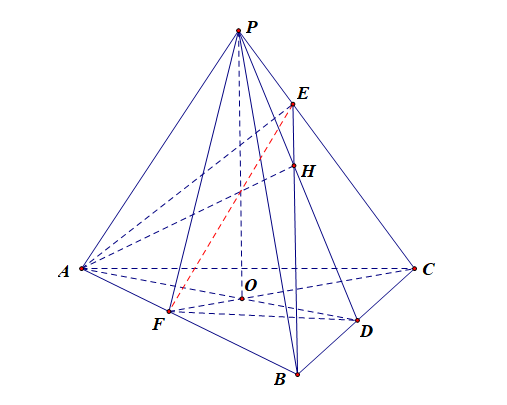
故\(\angle EFC\)为二面角\(H-AB-C\)的平面角，则由已知得\(\angle EFC=\cfrac{\pi}{6}\).

设正三角形\(ABC\)的边长为\(2x\)，则\(BD=FB=x\)，则\(CF=\sqrt{3}x\)，

在\(Rt\triangle CEF\)中，由于\(\angle CFE=\cfrac{\pi}{6}\)，故\(CE=\cfrac{\sqrt{3}}{2}x\)，\(EF=\cfrac{3}{2}x\)；

在\(Rt\triangle CEB\)中，可得\(BE^2=BC^2-CE^2=(2x)^2-(\cfrac{\sqrt{3}}{2}x)^2=\cfrac{13}{4}x^2\)，

且由于是正三棱锥，有\(BE=AE\)；

又在\(Rt\triangle PAF\)中，则\(PF^2==PA^2-AF^2=2^2-x^2=4-x^2\)，

则在\(Rt\triangle PEF\)中，\(PE^2=PF^2-EF^2=4-x^2-\cfrac{9}{4}x^2=4-\cfrac{13x^2}{4}\)，

由已知\(PA=2=PC\)，即\(PE+CE=PC=2\)，即\(\sqrt{4-\cfrac{13x^2}{4}}+\cfrac{\sqrt{3}}{2}x=2\)，

移项，得到\(\sqrt{4-\cfrac{13x^2}{4}}=2-\cfrac{\sqrt{3}}{2}x\)，两边平方，解得\(x=\cfrac{\sqrt{3}}{2}\)，

故可得\(AB=BC=AC=\sqrt{3}\)，\(BD=BF=\cfrac{\sqrt{3}}{2}\)，\(AD=\cfrac{\sqrt{3}}{2}\times\sqrt{3}=\cfrac{3}{2}\)，

则由点\(O\)为正三角形\(ABC\)的重心，得到\(AO=\cfrac{3}{2}\times \cfrac{2}{3}=1\)，

在\(Rt\triangle PAO\)中，\(PA=2\)，\(AO=1\)，故\(\angle PAO=\cfrac{\pi}{3}\).

即直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\)；

④两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\)；

分析：由上可知，线段\(EF\)为两条异面直线\(AB\)和\(PC\)的公垂线，

且\(EF=\cfrac{3}{2}x=\cfrac{3}{2}\times\cfrac{\sqrt{3}}{2}=\cfrac{3\sqrt{3}}{4}\)；

即两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\)；故④正确；

⑤直线 \(FD\) 与直线 \(PC\) 所成角的余弦值为 \(\cfrac{\sqrt{3}}{3}\)；

分析：由于点\(D\)， \(F\)分别是线段\(BC\)和\(AB\)的中点，故\(DF//AC\)，

则直线 \(FD\) 与直线 \(PC\) 所成角的也就是直线 \(AC\) 与直线 \(PC\) 所成的角，

由上可知是正三棱锥，故在\(\triangle PAC\)中，\(PA=PC=2\)，\(AC=AB=BC=\sqrt{3}\)，

故由余弦定理或者构造\(Rt\triangle\)可得到，\(\cos\angle PCA=\cfrac{\sqrt{3}}{4}\)，故④错误；

⑥三棱锥 \(P-ABC\) 的体积为 \(\cfrac{3}{4}\)；

分析：由上可知，\(PC=2\)，\(CD=\cfrac{\sqrt{3}}{2}\)，则\(PD^2=PC^2-CD^2=2^2-(\cfrac{\sqrt{3}}{2})^2=\cfrac{13}{4}\)，

则\(PO^2=PD^2-OD^2=\cfrac{13}{4}-\cfrac{1}{4}=3\)，即\(PO=\sqrt{3}\)，

故\(V_{P-ABC}=\cfrac{1}{3}\cdot S_{\triangle ABC}\cdot PO=\cfrac{1}{3}\cdot \cfrac{\sqrt{3}}{4}\cdot(\sqrt{3})^2\cdot \sqrt{3}=\cfrac{3}{4}\)，故⑥正确，

综上所述，正确的命题有：①③④⑥；

【北京人大附中高二试题】已知圆 \(O: x^{2}+y^{2}=1\)， 定点 \(M(3,0)\)， 过点 \(M\) 的直线 \(l\) 与圆 \(O\) 交于 \(P\) 、 \(Q\) 两点，\(P\) 、 \(Q\) 两点均在 \(x\) 轴的上方，如图， 若 \(OP\) 平分 \(\angle MOQ\)， 则直线 \(l\) 的方程为____________.

分析：由于\(P\) 、 \(Q\) 两点在圆上，且\(OP\) 平分 \(\angle MOQ\)，

故设 \(P(\cos\theta,\sin\theta)\)，则 \(Q(\cos2\theta,\sin2\theta)\)，又点 \(M(3,0)\)，

由\(k_{MP}=k_{MQ}\)，可得到\(\cfrac{\sin2\theta-0}{\cos2\theta-3}=\cfrac{\sin\theta}{\cos\theta-3}\)，

变形整理，得到\(\sin2\theta\cdot\cos\theta-3\sin2\theta=\sin\theta\cdot\cos2\theta-3\sin\theta\)，

即\(\sin2\theta\cdot\cos\theta-\sin\theta\cdot\cos2\theta=3\sin2\theta-3\sin\theta\)，

则\(\sin\theta=3\sin2\theta-3\sin\theta\)，即\(4\sin\theta=3\sin2\theta=3\times2\sin\theta\cdot\cos\theta\)，

由于\(\sin\theta\neq0\)，两边约去\(\sin\theta\)，得到\(\cos\theta=\cfrac{2}{3}\)，

故\(\sin\theta=\cfrac{\sqrt{5}}{3}\)，代入\(k_{MP}\)求得直线\(l\)的斜率

即\(k=\cfrac{\sin\theta}{\cos\theta-3}=\cfrac{\frac{\sqrt{5}}{3}}{\frac{2}{3}-3}=-\cfrac{\sqrt{5}}{7}\)

由点\(M(3,0)\)和斜率\(k=-\cfrac{\sqrt{5}}{7}\)可得，直线 \(l\) 的方程为\(y=-\cfrac{\sqrt{5}}{7}(x-3)\).

【北京人大附中高二试题】过点\((1，2)\)总可作两条直线与圆\(x^{2}+y^{2}+kx+2y+k^{2}-15=0\) 相切 ，则实数 \(k\) 的取值范围是____________.

分析：将圆\(x^{2}+y^{2}+kx+2y+k^{2}-15=0\) 整理为标准形式，

即\((x+\cfrac{k}{2})^2+(y+1)^2=16-\cfrac{3k^2}{4}\)，

由表达式可知，要想让圆存在，首先必须满足条件\(r^2>0\)， \(16-\cfrac{3k^2}{4}>0\)①；

作出示意图，如下所示，由图可知，

要想过点\((1，2)\)总可作两条直线与圆\(x^{2}+y^{2}+kx+2y+k^{2}-15=0\) 相切

则点\((1,2)\)必须始终在圆外，即必须满足数的形式，\(1+4+k+4+k^2-15>0\)②；

由此得到不等式组\(\left\{\begin{array}{l}{16-\cfrac{3k^2}{4}>0\quad ①}\\{1+4+k+4+k^2-15>0\quad ②}\end{array}\right.\)

解①得到，\(-\cfrac{8\sqrt{3}}{3}<k<\cfrac{8\sqrt{3}}{3}\)；解②得到，\(k<-3\)或\(k>2\)；

故得到所求范围，\(k\in (-\cfrac{8\sqrt{3}}{3},-3)\cup(2,\cfrac{8\sqrt{3}}{3})\)；

【北京人大附中高二试题】在平面直角坐标系 \(xOy\) 中， \(A\)， \(B\) 为 \(x\) 轴正半轴上的两个动点， \(P\)(异于原点 \(O\))为 \(y\) 轴上的一个定点. 若以\(AB\) 为直径的圆与圆 \(x^{2}+(y-2)^{2}=1\) 相外切，且 \(\angle APB\) 的 大小恒为定值 ， 则线段 \(OP\) 的长为 \(\sqrt{3}\)

分析：设点\(M(a,0)\)，圆\(M\) 的半径为\(r\)(变量)，\(OP=t\)(常量)，则有

由图可知，\(\tan \angle OPA=\cfrac{a-r}{t}\)， \(\tan\angle OPB=\cfrac{a+r}{t}\)

则\(\tan \angle APB=\tan(\angle OPB-\angle OPA)=\cfrac{\cfrac{a+r}{t}-\cfrac{a-r}{t}}{1+\cfrac{a^{2}-r^{2}}{t^{2}}}=\cfrac{2rt}{t^{2}+a^{2}-r^{2}}\)

又由于两圆外切，则\(\sqrt{a^{2}+4}=|r+1|\)，即\(a^{2}=(r+1)^{2}-4\)，代入上式得到，

\(\tan\angle APB=\cfrac{2rt}{t^{2}+2r-3}=\cfrac{2 t}{\frac{t^{2}-3}{r}+2}\)

由于\(\angle APB\) 的大小恒为定值， 故 \(t=\sqrt{3}\)

则 \(|OP|=\sqrt{3}\).

另解：\(\tan\angle APB=\cfrac{2t\cdot r}{2\cdot r+(t^{2}-3)}=\cfrac{2t\cdot r+0}{2\cdot r+(t^{2}-3)}\)，

令\(t^2-3=0\)， 故 \(t=\sqrt{3}\)，则\(|OP|=\sqrt{3}\).

【北京人大附中高二试题】如图，在平面直角坐标系 \(xOy\) 中，已知以\(M\)为圆心的圆\(M:\) \(x^{2}\)\(+\)\(y^{2}\)\(-12x\)\(-14y\)\(+\)\(60\)\(=0\) 及其上一点 \(A(2,4)\).

(1). 设圆 \(N\) 与 \(x\) 轴相切，与圆 \(M\) 外切, 且圆心 \(N\) 在直线 \(x=6\) 上, 求圆 \(N\) 的标准方程；

分析：由于\(N\) 在直线 \(x=6\) 上， 故设 \(N(6, n)\)，

由题可知，圆 \(N\) 与 \(x\) 轴相切，故圆 \(N\) 为 \(: (x-6)^{2}+(y-n)^{2}=n^{2}\)， \(n>0\)，

又圆 \(N\) 与圆 \(M\)外切设两圆的圆心分别为\(O_1\)、\(O_2\)，两圆的半径分别为\(R_1\)、\(R_2\)，则两圆外切\(\Leftrightarrow\) \(|O_1O_2|\)\(=\)\(R_1\)\(+\)\(R_2\)\(\quad\)，\(\odot M\)：\((x-6)^2+(y-7)^2=25\)，圆心坐标为\(M(6,7)\)；

故由两圆外切得到，\(|7-n|=|n|+5\)， 解得 \(n=1\)，

故得到圆 \(N\) 的标准方程为：\(\odot N\)：\((x-6)^2+(y-1)^2=1\)；

(2). 设平行于 \(OA\) 的直线 \(l\) 与圆 \(M\) 相交于\(B\)，\(C\) 两点， 且 \(BC=OA\) ，求直线 \(l\) 的方程；

分析：由题意得 \(OA=2\sqrt{5}\)， \(k_{OA}=2\)， 设\(l: y=2x+b\)，

则圆心\(M\)到直线\(BC：2x-y+b=0\)的距离 \(d=\cfrac{|2\times6-7+b|}{\sqrt{2^2+1^2}}=\cfrac{|5+b|}{\sqrt{5}}\)，

则 \(|BC|=2\sqrt{5^{2}-d^{2}}=2\sqrt{25-\cfrac{(5+b)^{2}}{5}}\)， \(BC=2\sqrt{5}\)，

即 \(2\sqrt{25-\cfrac{(5+b)^{2}}{5}}=2\sqrt{5}\)，解得 \(b=5\) 或 \(b=-15\)，

故直线\(l\) 的方程为 \(: y=2x+5\) 或 \(y=2x-15\).

(3). 设点 \(T(t, 0)\) 满足: 存在圆 \(M\) 上的两点 \(P\) 和 \(Q\)， 使得 \(\overrightarrow{TA}+\overrightarrow{TP}=\overrightarrow{TQ}\)， 求实数 \(t\) 的取值范围.

分析： 设 \(P(x_{1}, y_{1})\)， \(Q(x_{2}, y_{2})\)，

由于\(A(2,4)\)， \(T(t, 0)\)， 且\(\overrightarrow{TA}+\overrightarrow{TP}=\overrightarrow{TQ}\)，备注此处的向量表达式目的是从数的角度刻画\(P\)和\(Q\)两点满足的关系；\(\quad\).

即\((2-t,4)+(x_1-t,y_1)=(x_2-t,y_2)\)，

故 \(\left\{\begin{array}{l}{x_{2}=x_{1}+2-t}\\{y_{2}=y_{1}+4}\end{array}\right.\)①，

由于点 \(Q\) 在圆 \(M\)上， 故 \((x_{2}-6)^{2}+(y_{2}-7)^{2}=25\)②，

将①代入②， 得 \((x_{1}-t-4)^{2}+(y_{1}-3)^{2}=25\)，

即点\(P\)在圆心为\((t+4,3)\)，半径为\(5\)的圆上，

从而圆 \((x-6)^{2}+(y-7)^{2}=25\) 与圆 \([x-(t+4)]^{2}+(y-3)^{2}=25\) 有公共点设两圆的圆心分别为\(O_1\)、\(O_2\)，两圆的半径分别为\(R_1\)、\(R_2\)，且\(R_1>R_2\)，则两圆有公共点\(\Leftrightarrow\) \(R_1\)\(-\)\(R_2\)\(\leqslant\)\(|O_1O_2|\)\(\leqslant\)\(R_1\)\(+\)\(R_2\)；\(\quad\)，

故\(5-5\leqslant\sqrt{[(t+4)-6]^{2}+(3-7)^{2}}\leqslant 5+5\)，

解得 \(2-2\sqrt{21}\leqslant t\leqslant 2+2\sqrt{21}\)；

即实数 \(t\) 的取值范围为 \(t\in [2-2\sqrt{21},2+2\sqrt{21}]\)；

【北京人大附中高二11月月考第24题】已知四棱锥 \(T-ABCD\) 的底面是平行四边形，平面 \(\alpha\) 与直线 \(AD\)， \(TA\)， \(TC\) 分别交于点\(P\)， \(Q\)， \(R\) 且 \(\cfrac{AP}{AD}=\cfrac{TQ}{TA}=\cfrac{CR}{CT}=x\)，点 \(M\) 在直线 \(TB\) 上， \(N\) 为 \(CD\) 的中点，且直线 \(MN\)//平面\(\alpha\).

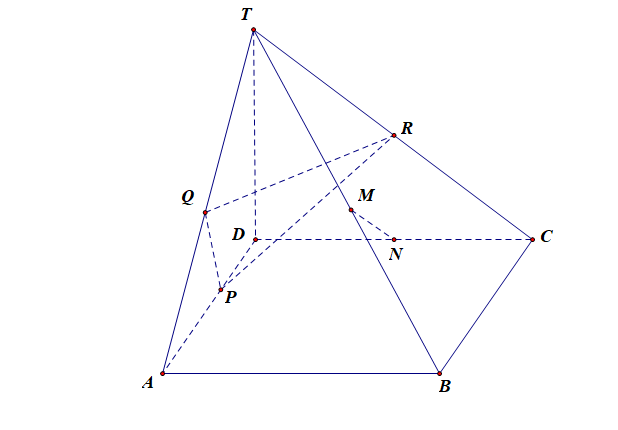
(1).设 \(\overrightarrow{TA}=\vec{a}\)，\(\overrightarrow{TB}=\vec{b}\)，\(\overrightarrow{TC}=\vec{c}\)，试用基底 \(\{\vec{a}，\vec{b}，\vec{c}\}\) 表示向量 \(\overrightarrow{TD}\);

分析： 由于\(\overrightarrow{TA}+\overrightarrow{TC}=\overrightarrow{TB}+\overrightarrow{TD}\)，

故 \(\overrightarrow{TD}=\bar{a}-\vec{b}+\vec{c}\)；

(2).证明: 四面体 \(TABC\) 中至少存在一个顶点, 从其出发的三条棱能够组成一个三角形;

证明： 不妨设 \(AB\) 是四面体\(TABC\) 中最长的棱，

则在 \(\triangle ABT\)中，有\(AT+TB>AB\)；在\(\triangle ABC\) 中， 有\(AC+CB>AB\)，

所以 \(AT+TB+AC+CB>2AB\)，\((AT+AC)+(TB+BC)>2AB\)，

所以 \(AT+AC\)与 \(TB+TC\) 中至少有一个大于\(AB\)从反面思考，如果两个都小于\(AB\)，则其和小于\(AB\)，不符合题意。\(\quad\)，

不妨取 \(AT+AC>AB\)，且按照设定，必然有\(AB+AC>AT\)，\(AB+AT>AC\)，

所以\(AT\)、\(AC\)、\(AB\) 能构成三角形.

(3).证明: 对所有满足条件的平面 \(\alpha\)，点 \(M\) 都落在某一条长为 \(\cfrac{\sqrt{5}}{2}TB\) 的线段上.

证明：设 \(\overrightarrow{TA}=\vec{a}\)， \(\overrightarrow{TB}=\vec{b}\)， \(\overrightarrow{T C}=\vec{c}\)，

由(1) 可知， \(\overrightarrow{TD}=\vec{a}-\vec{b}+\vec{c}\)，

由于\(\cfrac{AP}{AD}=\cfrac{TQ}{TA}=\cfrac{CR}{CT}=x\)，

所以 \(\overrightarrow{TQ}=x \vec{a}\)， \(\overrightarrow{TR}=(1-x)\vec{c}\)，

由于 \(\overrightarrow{AP}=x \overrightarrow{AD}\)，

所以\(\overrightarrow{TP}=(1-x) \vec{a}+x(\vec{a}+\vec{c}-\vec{b})=\vec{a}+x\vec{c}-x\vec{b}\)，

则\(\overrightarrow{QP}=\vec{a}+x \vec{c}-x \vec{b}-x \vec{a}=(1-x) \vec{a}+x \vec{c}-x \vec{b}\)，

则\(\overrightarrow{QR}=(1-x) \vec{c}-x \vec{a}=-x \vec{a}+(1-x) \vec{c}\)，

设 \(\overrightarrow{TM}=\lambda \overrightarrow{TB}=\lambda \vec{b}\)，

由于 \(\overrightarrow{TN}=\cfrac{1}{2}\overrightarrow{TC}+\cfrac{1}{2}\overrightarrow{TD}=\cfrac{1}{2} \vec{a}-\cfrac{1}{2} \vec{b}+\vec{c}\)，

\(\overrightarrow{NM}=\lambda \vec{b}-\cfrac{1}{2}\vec{a}-\vec{c}=-\cfrac{1}{2}\vec{a}+(\lambda+\frac{1}{2})\vec{b}-\vec{c}\)，

由于 \(\overrightarrow{NM}//\) 平面 \(PQR\)，

所以 存在实数 \(y\)， \(z\)， 使得 \(\overrightarrow{NM}=y\overrightarrow{QP}+z \overrightarrow{QR}\)，

所以 \(-\cfrac{1}{2}\vec{a}+(\lambda+\cfrac{1}{2}) \vec{b}-\vec{c}=y(1-x) \vec{a}-y x \vec{b}+y x \vec{c}-z x \vec{a}+z(1-x) \vec{c}\)，

\(=(y-xy-zx) \vec{a}-yx \vec{b}+(yx+z-xz) \vec{c}\)，

所以 \(\left\{\begin{array}{l}{y-xy-zx=-\cfrac{1}{2}}\\{-yx=\lambda+\cfrac{1}{2}}\\{yx+z-xz=-1}\end{array}\right.\)

消元可得 \((4\lambda+1)x^{2}-(4\lambda+3)\times+2\lambda+1=0\)，

当 \(\lambda=-\cfrac{1}{4}\)时，\(-2x+\cfrac{1}{2}=0\)，解得\(x=\cfrac{1}{4}\)，

当 \(\lambda \neq-\cfrac{1}{4}\)， 由于\(x\in R\)，

所以 \(\Delta=(4\lambda+3)^{2}-4(4\lambda+1)(2\lambda+1)\geqslant 0\)，

解得， \(-\cfrac{\sqrt{5}}{4} \leqslant \lambda \leqslant \cfrac{\sqrt{5}}{4}\)，

综上， \(-\cfrac{\sqrt{5}}{4} \leqslant \lambda \leqslant \cfrac{\sqrt{5}}{4}\). \(\quad\)且有\(| \cfrac{\sqrt{5}}{4}+\cfrac{\sqrt{5}}{4}|=\cfrac{\sqrt{5}}{2}\)，

故对所有满足条件的平面\(\alpha\)，点 \(M\) 都落在某一条长为 \(\cfrac{\sqrt{5}}{2}TB\) 的线段上.