在线|九月选填题

典例剖析

已知\(|z-1-i|=1\)且\(|z-3|\)最大，求\(z\)点的坐标。

分析：如图所示，\(|z-1-i|=1\)表示复平面内，以点\((1,1)\)为圆心，以\(1\)为半径的圆，

又由于\(|z-3|\)最大，则表示圆上的点到点\((3,0)\)的距离最远，换个视角，

即点\((3,0)\)到圆上的点的距离最远，故如图所示，应该是图中的点\(A\)；

由于\(k_{AB}=-\cfrac{1}{2}\)，故直线\(AB：x+2y-3=0\)，

和\((x-1)^2+(y-1)^2=1\)联立，求得点\(A(1-\cfrac{2\sqrt{5}}{5},1+\cfrac{\sqrt{5}}{5})\)，

即所求坐标为\((1-\cfrac{2\sqrt{5}}{5},1+\cfrac{\sqrt{5}}{5})\).

【北京人大附中高二阶段检测第8题】在四面体\(ABCD\)中，点\(P\)在平面\(ABC\)内，点\(Q\)在平面\(BCD\)内，且满足\(\overrightarrow{AP}=x\cdot\overrightarrow{AB}+y\cdot\overrightarrow{AC}\)，\(\overrightarrow{AQ}=s\cdot\overrightarrow{AB}+t\cdot\overrightarrow{AC}+u\cdot \overrightarrow{AD}\)，若\(\cfrac{x}{y}=\cfrac{s}{t}\)，则下面表述中，线段\(AQ\) 与\(DP\) 的关系是 【\(\quad\)】

$A$.$AQ$ 与$DP$ 所在直线是异面直线

$B$.$AQ$ 与$DP$ 所在直线平行

$C$.线段$AQ$ 与$DP$ 必然相交

$D$.线段$AQ$ 与$DP$ 延长后相交

分析：由题可知，向量\(\overrightarrow{AB}\)，\(\overrightarrow{AC}\)，\(\overrightarrow{AD}\)不共面，故以这三个向量为一组基底是合理的，用其线性组合就可以刻画表达空间内的任意一个向量，

由于\(\overrightarrow{AP}=x\cdot\overrightarrow{AB}+y\cdot\overrightarrow{AC}+0\cdot \overrightarrow{AD}\)，则向量\(\overrightarrow{AP}\)必在平面\(ABC\)内，且和向量\(\overrightarrow{AH}\)共线，

\(\overrightarrow{AQ}=s\cdot\overrightarrow{AB}+t\cdot\overrightarrow{AC}+u\cdot \overrightarrow{AD}\)，则\(\overrightarrow{AQ}\)必在平面\(ADH\)内，

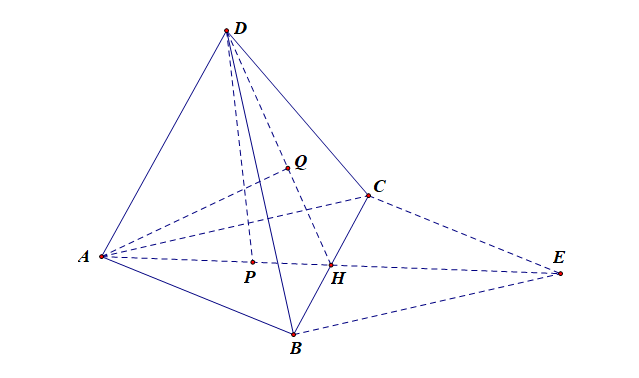
由于\(\cfrac{x}{y}=\cfrac{s}{t}\)，不妨采用特殊化策略，将其特殊化为\(x=y=s=t=\cfrac{1}{2}\)，\(u=1\)，则点\(P\)必落在点\(H\)上，点\(Q\)必在以\(AD\)和\(AH\)为一组邻边所构成的平行四边形的对角线上，故线段\(AQ\)与\(DP\)必然相交。故选\(C\).

【北京人大附中高二阶段检测第9题】在三棱锥\(T-ABC\)中，\(TA\)，\(TB\)，\(TC\)两两垂直，点\(T\)在平面\(ABC\)上的射影为\(D\)，\(O\)为三棱锥\(T-ABC\)内任意一点，连接\(OA\)，\(OB\)，\(O C\)，\(OT\)并延长，交对面于点\(A'\)， \(B'\)，\(C'\)，\(T'\)；则:

①. 点\(D\)是\(\triangle ABC\)的垂心；

②. \(TA\perp BC\)，\(TB\perp AC\)，\(TC\perp AB\)；

③. \(\triangle ABC\)是锐角三角形；

④. \(S_{\triangle ABC}^{2}=\frac{1}{3}(S_{\triangle TAB}^{2}+S_{\triangle TAC}^{2}+S_{\triangle TBC}^{2})\)

⑤. \(\frac{OA'}{AA'}+\frac{OB'}{BB'}+\frac{OC'}{CC'}+\frac{OT'}{TT'}=1\)

⑥. \(\frac{1}{TD^{2}}=\frac{1}{TA^{2}}+\frac{1}{TB^{2}}+\frac{1}{TC^{2}}\)

以上结论中正确结论有【\(\quad\)】个。

$A.2$ $B.3$ $C.4$ $D.5$

分析：首先需要注意直三面角的两种常用配图；

对于②而言，由于\(TA\)，\(TB\)，\(TC\)两两垂直，故容易证明\(TA\perp\)平面\(TBC\)，故可以证明\(TA\perp BC\)，同理可证，\(TB\perp AC\)，\(TC\perp AB\)；故②正确；

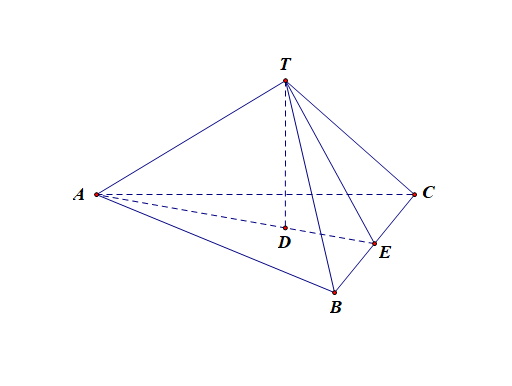
过\(T\)作\(TD\perp\)平面\(ABC\)于点\(D\)，则由\(BC\perp TD\)，\(BC\perp TA\)，可知\(TD\perp\)平面\(TAD\)，

连接\(AD\)并延长交\(BC\)于点\(E\)，连接\(TE\)，则可知，\(AT\perp TE\)，\(TE\perp BC\)，\(AE\perp BC\)；

同理，\(CD\perp AB\)；\(BD\perp AC\)；即点\(D\)为\(\triangle ABC\)的垂心；故①正确；

对于③而言，设\(TA=a\)，\(TB=b\)，\(TC=c\)，则\(AB=a^2+b^2\)，\(BC=b^2+c^2\)，\(AC=a^2+c^2\)，

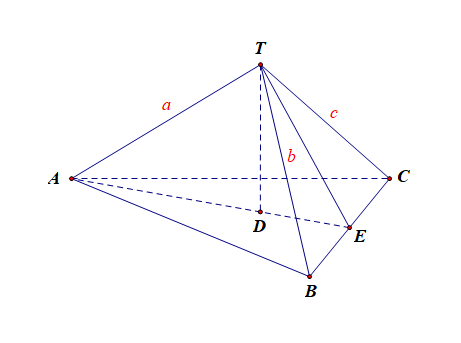
则\(\cos \angle ABC=\cfrac{(a^2+b^2)+(b^2+c^2)-(a^2+c^2)}{2\cdot AB\cdot BC}=\cfrac{2b^2}{2\cdot AB\cdot BC}>0\)，

故\(\angle ABC\)为锐角，同理，\(\angle BCA\)为锐角，\(\angle ACB\)为锐角，故\(\triangle ABC\)是锐角三角形；

当然，也可以使用动态的观点，直接观察得到\(\triangle ABC\)是锐角三角形；

对于④而言，例题7；

对于⑤而言，例题19，20；

对于⑥而言，设\(TA=a\)，\(TB=b\)，\(TC=c\)，由于点\(D\)为\(\triangle ABC\)的垂心，且\(BC\perp\)平面\(TAE\)；

在\(\triangle TBC\)中，由等面积法可知，\(\frac{1}{2} TE\cdot \sqrt{b^2+c^2}=\frac{1}{2}bc\)，即\(TE=\frac{bc}{\sqrt{b^2+c^2}}\)；

又在\(\triangle ABC\)中，由等面积法可知，\(\frac{1}{2} AE\cdot BC=\frac{1}{2} AE\cdot\sqrt{b^2+c^2}=S_{\triangle ABC}\)；

又由于\(S_{\triangle ABC}^2=S_{\triangle TAB}^2+S_{\triangle TBC}^2+S_{\triangle TAC}^2=\frac{1}{4}(a^2b^2+b^2c^2+a^2c^2)\)，

故\(S_{\triangle ABC}=\frac{1}{2}\sqrt{a^2b^2+b^2c^2+a^2c^2}\)，

即\(AE\cdot\sqrt{b^2+c^2}=\sqrt{a^2b^2+b^2c^2+a^2c^2}\)，故\(AE=\frac{\sqrt{a^2b^2+b^2c^2+a^2c^2}}{\sqrt{b^2+c^2}}\)；

在\(\triangle ATE\)中，由等面积法可知，\(\frac{1}{2} AE\cdot TD=\frac{1}{2} AT\cdot TE\)，

即\(\frac{\sqrt{a^2b^2+b^2c^2+a^2c^2}}{\sqrt{b^2+c^2}}\times TD=a\times \frac{bc}{\sqrt{b^2+c^2}}\)，

即得到，\(TD^2\cdot (a^2b^2+b^2c^2+a^2c^2)=a^2b^2c^2\)；

即\(\frac{1}{TD^2}=\cfrac{a^2b^2+b^2c^2+a^2c^2}{a^2b^2c^2}=\cfrac{1}{a^2}+\cfrac{1}{b^2}+\cfrac{1}{c^2}=\frac{1}{TA^2}+\frac{1}{TB^2}+\frac{1}{TC^2}\)，故⑥是正确的；

综上所述，正确的命题有①②③⑤⑥，故选\(D\)；

【北京人大附中高二阶段检测第10题】棱长为\(2\)的正方体\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，\(E\)为棱\(CC_{1}\)的中点，点\(P\)，\(Q\)分别为面\(A_{1}B_{1}C_{1}D_{1}\)和线段\(B_{1}C\)上的动点，则\(\triangle PEQ\)周长的最小值为【\(\quad\)】

$A.2\sqrt{2}$ $B.\sqrt{10}$ $C.\sqrt{11}$ $D.2\sqrt{3}$

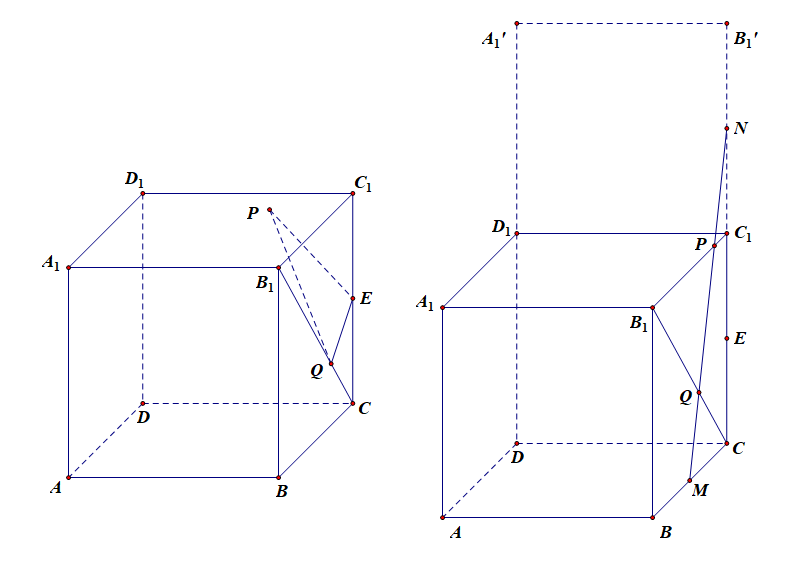
分析：由题目可知，点\(P\)和点\(Q\)为两个动点，我们可以先假定点\(Q\)不动，令点\(P\)在平面\(A_1B_1C_1D_1\)上任意运动，很显然，当点\(P\)在线段\(B_1C_1\)上运动时，\(\triangle PEQ\)周长才可能取得最小值，故点\(P\)在线段\(B_1C_1\)上运动。

此时，将上底面\(A_1B_1C_1D_1\)绕 轴\(C_{1}D_{1}\) 旋转\(90^{\circ}\)展开，求得点\(E\)关于\(B_1C\)的对称点\(M\)，则\(QM=QE\)，求得点\(E\)关于\(B_1C_1\)的对称点\(N\)，则\(PE=PN\)；此时直接连接\(MN\)，由于\(\triangle PEQ\)的周长\(=PE+QE+PQ=QM+PQ+PN\)，则\(MN\)即为\(\triangle PEQ\)周长的最小值；

此时，\(CN=3\)，\(CM=1\)，故由勾股定理得到\(MN=\sqrt{1^2+3^2}=\sqrt{10}\)，故选\(B\).

【北京人大附中高二阶段检测第12题】在平行六面体\(ABCD-A'B'C'D'\)中，\(\angle BAD\)\(=\)\(\angle A'AB\)\(=\)\(\angle A'AD\)\(=\)\(60^{\circ}\)，\(AB=3\)，\(AD=4\)，\(AA'=5\)，\(AC'\)=________.

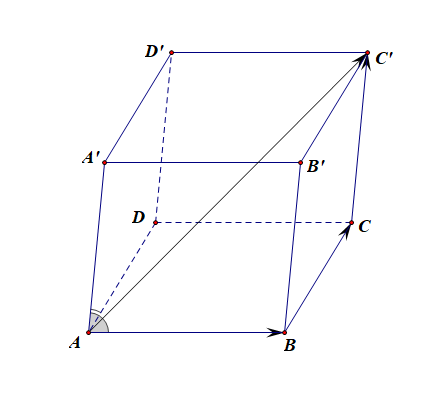
分析：由于\(|\overrightarrow{AC'}|=|\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC'}|\)，

则\(|\overrightarrow{AC'}|^2=|\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC'}|^2\)

\(=|\overrightarrow{AB}|^2+|\overrightarrow{BC}|^2+|\overrightarrow{CC'}|^2+2\overrightarrow{AB}\cdot \overrightarrow{BC}+2\overrightarrow{BC}\cdot\overrightarrow{CC'}+2\overrightarrow{AB}\cdot \overrightarrow{CC'}\)，

\(=3^2+4^2+5^2+2\times3\times4\times(\cfrac{1}{2})+2\times4\times5\times(\cfrac{1}{2})+2\times3\times5\times(\cfrac{1}{2})=97\)

\(|\overrightarrow{AC'}|=\sqrt{97}\)；

【北京人大附中高二阶段检测第14题】如图，在棱长均为\(2\)的正三棱柱当题目已知了正三棱柱，则我们只能知道上下底面为正三角形，并不能知道侧棱长和底面边长的关系，当告诉棱长均为\(2\)时，则此正三棱柱的侧棱长和底面边长是相等的。\(\quad\)\(ABC-A_1B_1C_1\)中，点\(M\)是侧棱\(AA_{1}\)的中点，点\(P\)、\(Q\)分别是侧面\(BCC_1B_1\)、底面\(ABC\)内的动点，且\(A_1P//\)面\(BCM\)，\(PQ\perp\)面\(BCM\)，则点\(Q\)的轨迹的长度为______________.

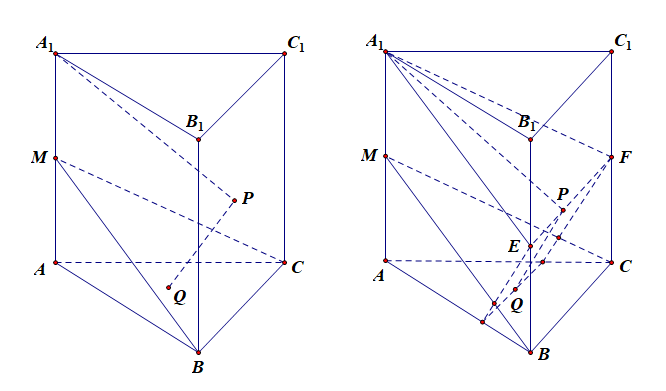
解：由于点\(P\)是侧面\(BCC_1B_1\)内的动点，且\(A_1P//\)平面\(BCM\)，

则\(P\)点的轨迹是过点\(A_1\)与平面\(MBC\) 平行的平面与侧面\(BCC_1B_1\)的交线\(EF\)，

\(Q\)是底面\(ABC\)内的动点，且\(PQ\perp\) 平面\(BCM\)，

则点\(Q\)的轨迹是经过直线\(EF\)与平面\(MBC\)垂直的平面与平面\(ABC\)相交的线段\(m\)，

即点\(Q\)的轨迹是线段\(m\)，以下说明线段\(m\)经过\(\triangle ABC\)的重心，取点\(P\)的一个特殊位置说明；

取点\(P\)为线段\(EF\)的中点，则点\(P\)在\(BC\)上的垂足\(P'\)为线段\(BC\)的中点，

由于\(\triangle ABP'\)为\(Rt\triangle\)，\(AB=2\)，\(BP'=1\)，则\(AP'=\sqrt{3}\)，故\(MP'=2\)，

由于\(\triangle MPP'\)为\(Rt\triangle\)，且\(PO\perp MP'\)，由等面积法可知，\(PO=\cfrac{\sqrt{3}}{2}\)，

由于\(\triangle QPP'\)为\(Rt\triangle\)，且\(PQ\perp OP'\)，由射影定理可知，\(PQ=\cfrac{2}{\sqrt{3}}=\cfrac{2\sqrt{3}}{3}\)，

由勾股定理可得，\(P'Q=\sqrt{(\cfrac{2}{\sqrt{3}})^2-1^2}=\cfrac{\sqrt{3}}{3}\)，\(AP'=\sqrt{3}\)，

故线段\(m\)必然经过\(\triangle ABC\)的重心，且与\(BC\)平行；

由正三棱柱\(ABC-A_1B_1C_1\)中的棱长均为\(2\)，故线段\(m\)的长为：\(\cfrac{2}{3}\times 2=\cfrac{4}{3}\).

【北京人大附中高二阶段检测第15题】正方体\(ABCD-A_{1}B_{1}C_{1}D_{1}\)的棱长为\(1\)，动点\(M\)在线段\(CC_{1}\)上，动点\(P\)在平面\(A_{1}B_{1}C_{1}D_{1}\)上，且\(AP\perp\)平面\(MBD_{1}\).

(1).当点\(M\)与点\(C\)重合时，线段\(AP\)的长度为__________.

分析：建立如图所示的空间直角坐标系，

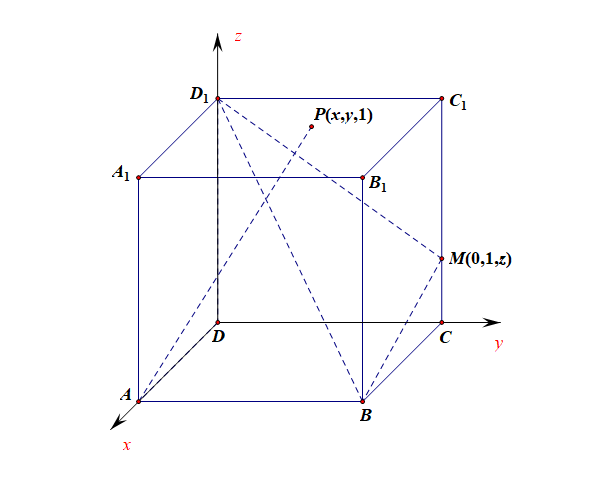
则点\(A(1,0,0)\)，点\(M(0,1,z)\)，点\(P(x,y,1)\)，点\(B(1,1,0)\)，点\(D_1(0,0,1)\)，

则\(\overrightarrow{D_1B}=(1,1,-1)\)，\(\overrightarrow{D_1M}=(0,1,z-1)\)，设平面\(MBD_1\)的法向量为\(\vec{v}=(p,q,k)\)，

则有\(\left\{\begin{array}{l}{\overrightarrow{D_1B}\cdot \vec{v}=0}\\{\overrightarrow{D_1M}\cdot \vec{v}=0}\end{array}\right.\)，即\(\left\{\begin{array}{l}{p+q-k=0}\\{q+k(z-1)=0}\end{array}\right.\)

解得，\(q=k(1-z)\)，\(p=kz\)，故法向量\(\vec{v}=(kz,k(1-z),k)\)，简化为\(\vec{v'}=(z,1-z,1)\)；

由于\(AP\perp\)平面\(MBD_{1}\)，则\(\overrightarrow{AP}//\vec{v}\)，又由于\(\overrightarrow{AP}=(x-1,y,1)\)，

故\(\cfrac{x-1}{z}=\cfrac{y}{1-z}=\cfrac{1}{1}\)，即\(\overrightarrow{AP}=(z,1-z,1)\)，当点\(M\)与点\(C\)重合时，\(z=0\)，

此时\(\overrightarrow{AP}=(0,1,1)\)，故\(\overrightarrow{AP}^2=0^2+1^2+1^2=2\)，

故\(|AP|=\sqrt{2}\)。

(2).线段\(AP\)长度的最小值为__________.

分析：由于\(\overrightarrow{AP}=(z,1-z,1)\)，\(z\in [0,1]\)

则\(\overrightarrow{AP}^2=z^2+(1-z)^2+1^2=2z^2-2z+2=2(z-\cfrac{1}{2})^2+\cfrac{3}{2}\)，

故当\(z=\cfrac{1}{2}\)时， \([\overrightarrow{AP}^2]_{min}=\cfrac{3}{2}\)，

故线段\(AP\)的最小值为\(\sqrt{\cfrac{3}{2}}=\cfrac{\sqrt{6}}{2}\).