符号法则及应用
符号法则，是我们在初中就学习过的内容，但高中经常使用，只是我们不太注意总结而已。
符号法则
符号语言：$ab=0\Leftrightarrow $ 自然语言：\(a=0\)或\(b=0\)；
符号语言：$ab\neq 0\Leftrightarrow $ 自然语言：\(a\neq 0\)且\(b\neq0\)；
符号语言：$ab\ge 0\Leftrightarrow $ 自然语言：\(\begin{cases}a\ge 0\\b\ge0 \end{cases}\)或\(\begin{cases}a\leq 0\\b\leq 0 \end{cases}\)；
符号语言：$ab\leq 0\Leftrightarrow $ 自然语言：\(\begin{cases}a\ge 0\\b\leq 0 \end{cases}\)或\(\begin{cases}a\leq 0\\b\ge 0 \end{cases}\)；
符号语言：\(a^2+b^2=0\Leftrightarrow\) 自然语言：\(a=0\)且\(b=0\)； 自然语言：\(a、b\)全为零；
符号语言：\(a^2+b^2\neq0\Leftrightarrow\) 自然语言：\(a\neq 0\)或\(b\neq 0\)； 自然语言：\(a、b\)不全为零；
符号语言：\(a>0,b>0\) $\Rightarrow $ 自然语言：\(a+b>0\)； 即正+正=正；
符号语言：\(a<0,b<0\) $\Rightarrow $ 自然语言：\(a+b<0\)； 即负+负=负；
解不等式中
分析：由题目可知，\(\left\{\begin{array}{l}{x-1>0}\\{f'(x)>0}\end{array}\right.\)或\(\left\{\begin{array}{l}{x-1<0}\\{f'(x)<0}\end{array}\right.\)
则得到，当\(x>1\)时，\(f'(x)>0\)，即函数\(f(x)\)在区间\((1，+\infty)\)上单调递增；
当\(x<1\)时，\(f'(x)<0\)，即函数\(f(x)\)在区间\((-\infty，1)\)上单调递减；
法1：穿根法，略；
法2：分析，原不等式等价于\(\left\{\begin{array}{l}{x^2-3x+2>0}\\{x+1<0}\end{array}\right.\)或\(\left\{\begin{array}{l}{x^2-3x+2<0}\\{x+1>0}\end{array}\right.\)
解集为\((-\infty，-1)\cup(1，2)\)；
不等式性质中
用图像解不等式
解法思路：利用条件先做出抽象函数的图像，然后读图解不等式
法1：自己作图如右，读图即可解答，解集为\((-1，0)\cup(1，3)\)；
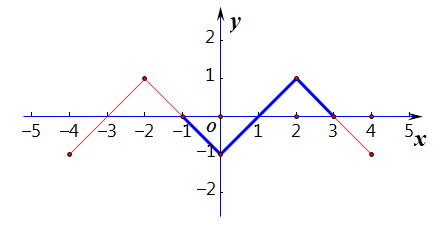
法2：利用积的符号法则求解，
原不等式等价于\(\begin{cases}x>0\\f(x)>0\end{cases}\)或\(\begin{cases}x<0\\f(x)<0\end{cases}\)，
读图即可解答，解集为\((-1，0)\cup(1，3)\)；
感悟反思：1、学图像，用图像，天经地义。2、熟练掌握分段函数的图像，对解题很有帮助。
分析：由于\(f(x+1)\)为偶函数，故其满足\(f(-x+1)=f(x+1)\)，则函数\(f(x)\)的对称轴为\(x=1\)，
可以先做出函数\(y=f(x+1)\)的示意图，再向右平移一个单位得到函数\(y=f(x)\)的示意图如下，
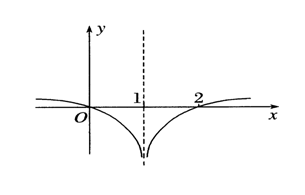
不等式\((x-1)\cdot f(x)\leqslant 0\)可化为\(\left\{\begin{array}{l}{x>1}\\{f(x)\leqslant 0}\end{array}\right.\)或\(\left\{\begin{array}{l}{x<1}\\{f(x)\geqslant 0}\end{array}\right.\)
解读图像可知，解集为\(\{x\mid x\leqslant 0\)或\(1<x\leqslant 2\}\)，故\(x\in (-\infty，0]\cup(1，2]\).
解：令 \(h(x)=x\cdot f(x)\)，任意 \(x_1,x_2\in(0,+\infty)\)，\(x_1\neq x_2\)，
则 \(\cfrac{h(x_1)-h(x_2)}{x_1-x_2}=\cfrac{x_1f(x_1)-x_2f(x_2)}{x_1-x_2}<0\)，
故函数 \(h(x)\) 在 \((0,+\infty)\)上单调递减，且满足 \(h(2)=0\)，且 \(h(x)=x\cdot f(x)\)为偶函数[奇x奇=偶]，
故做出满足题意的函数 \(h(x)\) 的简图如下：
由图象可知，当\(x\in(-\infty,-2)\) 时，\(h(x)=xf(x)<0\)，\(x<0\)，故 \(f(x)>0\)，
当\(x\in(-2,0)\) 时，\(h(x)=xf(x)>0\)，\(x<0\)，故 \(f(x)<0\)，
当\(x\in(0,2)\) 时，\(h(x)=xf(x)>0\)，\(x>0\)，故 \(f(x)>0\)，
当\(x\in(2,+\infty)\) 时，\(h(x)=xf(x)<0\)，\(x>0\)，故 \(f(x)<0\)，
故 不等式 \(f(x)<0\) 的解集为\((-2,0)\cup(2,+\infty)\) .
[引申]：①本题目是已知乘积的符号，求因子的符号；②还可以求解 \(xf(x)>0\)，\(\cfrac{f(x)}{x}>0\) .
大小比较中
分析：由于\(a_1，a_2\in (0，1)\)，则\(a_1-a<0\)，\(a_2-1<0\)，
\(M-N=a_1a_2-(a_1+a_2-1)=a_1a_2-a_1-a_2+1=(a_1-1)(a_2-1)>0\)，故\(M>N\).
导数的单调性中
用不等式性质判断导函数正负
分析：\(f'(x)=\sin x+x\cdot\cos x-\sin x=x\cdot\cos x\)；
在同一坐标系中，做出函数\(y=x\)和\(y=\cos x\)的图像，\(x\in (-\pi,\pi)\)，
由符号法则可知，单调递增区间为\((-\pi,-\cfrac{\pi}{2})\)和\((0,\cfrac{\pi}{2})\)；
单调递减区间为\((-\cfrac{\pi}{2}，0)\)和\((\cfrac{\pi}{2},\pi)\)；
分析：定义域为\(R\)，\(f'(x)=1\cdot e^x+(x-2)\cdot e^x+2a(x-1)=e^x(x-1)+2a(x-1)=(x-1)(e^x+2a)\)，
在同一个坐标系中做出函数\(y=x-1\)[定图]和函数\(y=e^x+2a\)[动图]的图像，
根据动图\(y=e^x+2a\)是否与\(x\)轴有交点分类讨论如下：[1]
①当\(2a\ge 0\)时，即\(a\ge 0\)时，恒有\(e^x+2a>0\)，
当\(x\in (-\infty，1)\)上时，\(x-1<0\) ，则\(f'(x)=(e^x+2a)(x-1)<0\)，故\(f(x)\)单调递减，
当\(x\in (1，+\infty)\)上时，\(x-1>0\) ，则\(f'(x)=(e^x+2a)(x-1)>0\)，故\(f(x)\)单调递增，
当\(2a<0\)时，即\(a<0\)时，\(y=e^x+2a\)与\(x\)轴有交点，令\(e^x+2a=0\)，解得\(x=ln(-2a)\)，
然后针对\(ln(-2a)\)与\(1\)的大小关系继续细分如下，主要是\(ln(-2a)\)和\(1\)分别是两个因子函数的零点；
②当\(ln(-2a)<1\)时，即\(-\cfrac{e}{2}<a<0\)时，
当\(x\in(-\infty，ln(-2a))\)时，\(e^x+2a<0\)，\(x-1<0\)，则\(f'(x)>0\)，\(f(x)\)单调递增；
当\(x\in(ln(-2a)，1)\)时，\(e^x+2a>0\)，\(x-1<0\)，则\(f'(x)<0\)，\(f(x)\)单调递减；
当\(x\in(1，+\infty)\)时，\(e^x+2a>0\)，\(x-1>0\)，则\(f'(x)>0\)，\(f(x)\)单调递增；
③当\(ln(-2a)=1\)时，即\(a=-\cfrac{e}{2}\)时，
当\(x\in(-\infty，1)\)时，\(e^x+2a<0\)，\(x-1<0\)，则\(f'(x)>0\)，\(f(x)\)单调递增；
当\(x\in(1，+\infty)\)时，\(e^x+2a>0\)，\(x-1>0\)，则\(f'(x)>0\)，\(f(x)\)单调递增；
即\(x\in (-\infty，+\infty)\)时，恒有\(f'(x)\ge 0\)，当且仅当\(x=1\)时取到等号，故\(f(x)\)单调递增；
④当\(ln(-2a)>1\)时，即\(a<-\cfrac{e}{2}\)时，
当\(x\in(-\infty，1)\)时，\(e^x+2a<0\)，\(x-1<0\)，则\(f'(x)>0\)，\(f(x)\)单调递增；
当\(x\in(1，ln(-2a))\)时，\(e^x+2a<0\)，\(x-1>0\)，则\(f'(x)<0\)，\(f(x)\)单调递减；
当\(x\in(ln(-2a)，+\infty)\)时，\(e^x+2a>0\)，\(x-1>0\)，则\(f'(x)>0\)，\(f(x)\)单调递增；
综上所述，
当\(a<-\cfrac{e}{2}\)时，单增区间为\((-\infty，1)\)和\((ln(-2a)，+\infty)\)，单减区间为\((1，ln(-2a))\)；
当\(a=-\cfrac{e}{2}\)时，只有单增区间为\((-\infty，+\infty)\)；
当\(-\cfrac{e}{2}<a<0\)时，单增区间为\((-\infty，ln(-2a))\)和\((1，+\infty)\)，单减区间为\((ln(-2a)，1)\)；
当\(a\ge 0\)时，单减区间为\((-\infty，1)\)，单增区间为\((1，+\infty)\)；
判断单调性
- 用图像确定\(f'(x)\)的正负，确定\(f(x)\)的单调性，
分析：由图可知，
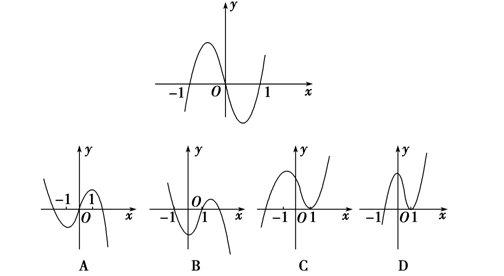
当\(x<-1\)时，\(y<0\)，故由符号法则可知\(f'(x)>0\)；
当\(-1<x<0\)时，\(y>0\)，故由符号法则可知\(f'(x)<0\)；
当\(0<x<1\)时，\(y<0\)，故由符号法则可知\(f'(x)<0\)；
当\(x>1\)时，\(y>0\)，故由符号法则可知\(f'(x)>0\)；
从而可知当\(x<-1\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；
当\(-1<x<1\)时，\(f'(x)<0\)，\(f(x)\searrow\)；
当\(x>1\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；故选C。
充要条件中
分析：当\(a=0\)时，即使\(a-b\)为正，为负，为零，都有\((a-b)a^2\geqslant 0\)，即由\((a-b)a^2\geqslant 0\)不能推出\(a\geqslant b\)，即充分性不成立；
当\(a\geqslant b\)时，即\(a-b\geqslant 0\)，由于\(a^2\geqslant 0\)，则有\((a-b)a^2\geqslant 0\)，故必要性成立；故选\(B\);
线性规划中
给定点 \(P(x_1,y_1)\) 、点 \(Q(x_2,y_2)\) 和直线 \(l：Ax+By+C=0\)，
点 \(P\)，点\(Q\) 在直线 \(l\) 的同侧的充要条件是\((Ax_1+By_1+C)(Ax_2+By_2+C)>0\)；
点 \(P\)，点\(Q\) 在直线 \(l\) 的异侧的充要条件是\((Ax_1+By_1+C)(Ax_2+By_2+C)<0\)；
不等式\((x-2y+1)(x+y-3)\leqslant 0\)在坐标系中表示的区域(用阴影部分表示)；
注意分类标准和书写顺序，
先令\(2a=0\)，确定函数\(y=e^x\)的位置，然后让\(2a>0\)，再确定\(y=e^x+2a\)的位置，发现这两种情形下的\(y=e^x+2a>0\)恒成立，故可以合二为一；
等讨论完了这种情形后，在讨论\(2a<0\)，很显然\(2a\geqslant 0\)要简单一些，故首先书写，先确定拿到一部分成绩，稳定心神； ↩︎
