《松本行弘的程序世界》读书笔记（下）——文字编码、整数、浮点小数
先贴上上一篇博客：这些基础知识你都了解吗？——《松本行弘的程序世界》读书笔记（上）
上一篇讲到：
- 面向对象
- 设计模式
- ajax
- MVC和猴子补丁
这一篇讲《松本行弘的程序世界》书中提到的编码、正则和数字。
7. 文字编码
7.1 理解编码
计算机只能处理二进制数据，从计算机被发明出来它是这样，到现在还是这样。那么我们要让这个只能识别“010101...”二进制的家伙去处理文字，该怎么办呢？——把文字表示成二进制。大家可以查看unicode（下文将介绍unicode）编码表，看看其中中文编码那一块，比如，16进制的4e07表示“万”字：
说到这里让我想起来，平时我们在新闻留言、QQ聊天或者发短信的时候，可以发一些表情——
，大家可能都知道这些表情是用一些特殊的字符串规定好的。其实，这就是一个简单的表情编码，和计算机中文字编码成二进制一个道理。
7.2 ASCII码
当初计算机是美国人发明的，最早也在美国被应用。美国人用英语，所谓的字符只有26个英文字母，大小写都算上，也不过52个，在算上键盘上那些乱七八糟的标点符号，最多100来个。于是他们发明了用7位二进制数构成的编码表——ASCII码。2的7次方=128。ASCII码可表示128个字符。计算机中8位二进制是一个字节，还能剩下一位，用于附加错误码（作者：不知错误码为何意？？）
上图中，用二进制数“1000001”表示的是字母“A”，十进制是65，咱们学C语言的时候，估计都能背过——'A'转换成int是65，现在知道什么意思了吧。。。
下图是ASCII码对应的值（十进制表示）：
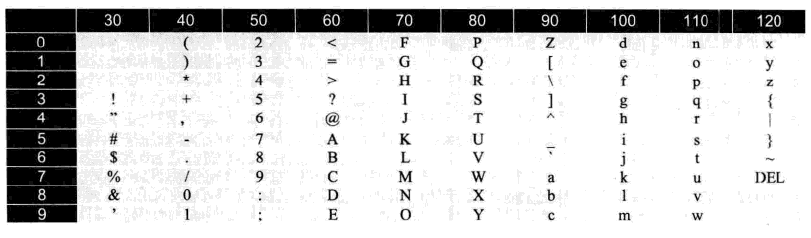
7.3 unicode字符集
世界上的文字有很多种，除了用A-Z表示的文字之外，还有许多欧洲、亚洲的文字是用其他图形表示的，比如咱们的中文（简体和繁体还不一样）。于是，ASCII码不能满足要求之后，有出现了很多种编码方式，例如中国的GB2312字符集。不过现在业界越来越统一到unicode字符集中。所以，就简单介绍unicode字符集。
ASCII码用7位二进制，可表示128个字符，而最初的unicode字符集用16位二进制表示，2的16次方=65536，可表示6万多个字符。unicode字符集最初的设计者预计6W多个字符足以表示世界上所有语言文字了，可惜他们错了。后来unicode字符集又扩充到了21位。
从网上可以查到所有unicode编码表的内容，以下是截取的一个片段。例如，汉字“万”的编码是16进制数 4e07：
7.4 unicode的字符编码方式
虽然unicode字符集将世界上的文字字符全部统一了编码，但是这个编码的存储方式，却又分为好几种，例如大家常见的UTF-8、UTF-16、UTF-32。
例如，汉字“万”的编码值是16进制数 4e07 ，但是通过UTF-8计算出的存储结构和UTF-16是不一样的。所以，如果用UTF-16的方式去解析UTF-8编码的数据，可能会出现乱码。
至于每种编码方式是怎样的，这里就不再详细介绍了。其实书中也只是讲了一点皮毛。大家了解即可。
8 正则表达式
我接触正则表达式是在学习js中接触的，js应用正则表达式比较简单，但是正则表达式本身的语法却很复杂。
后来看jQuery源码，被sizzle这块的正则表达式给完全搞晕了，到现在都没梳理好。
书中介绍的无非就是正则表达式的若干语法，以及Ruby如何支持。
其实学习正则表达式不用看这个，推荐一个：正则表达式30分钟入门教程（提醒：说30分钟是忽悠你，用俩小时全部看完并理解，就不错了！）
9. 整数与浮点小数
整数和浮点小数，是程序开发中最常用的类型之一。如果你觉得程序对数字的操作非常简单，无非就是加减乘除，那么请你耐心看完下面的文字。
9.1 整数是有范围的
在C、C++、C#等静态类型的语言中，int一般表示32位整数，也就是用32个二进制数表示一个整数，除去一个符号位，int所能表现的最大整数是有限的。
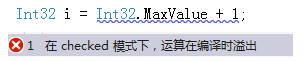
C#中，int32 和 int64 分别表示不同位数的整数，都有最大值和最小值的标志：
如果程序中的数字，超过了最大值，无法通过编译，提示溢出。同理，如果运行时出现了这样的情况，也会抛出异常。
另外，不光整数有范围。浮点小数也有范围大小，原理一样。
不过浮点小数还有其他要说的内容，下文介绍。
9.2 为何Ruby中的整数没有范围
任何语言都无法从根本上行使整数没有范围。Ruby是动态类型的语言，当他遇到数字超过单个整数范围时，它会把这个数分多个整数存储。不过这一切都是Ruby自动帮你完成的，所以在你看来，你认为Ruby的整数大小是无限制的。
这是一种技巧，类似于数据库的分表存储。
9.3 浮点小数的误差
其实我从很早以前就注意到，javascript中：0.1 + 0.2 = 0.30000000000000004 ，当时只是单纯的认为js对小数的计算有误差，以后得注意。但是看完书中本章节，发现不对。不光js，所以语言都会有误差。以C#为例：
大家可以从上图中很清楚的看到答案。程序第一行，虽然C#输出的是 0.1 + 0.2 = 0.3 ，但是从下面的程序可以看出，这里的0.3只不过是个近似值。
针对浮点小数的这些计算的误差，各个程序也都给出了他们认为的可控制的范围。例如，C#的single类型（即float类型）中，允许误差的可控范围如下图：
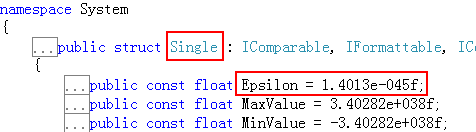
意思就是说，只要在这个范围之内，就不认为有误差。但是很遗憾，我还没有用到过这个属性。。。先了解一下吧。
9.4 计算机如何处理小数
上文说了半天的误差，下面解释计算机中为何对小数处理会产生误差。原因还是一句话：计算机只能处理二进制。
所有的整数，都可以用二进制无误差的表示出来，例如：65 --> 1000001，10 --> 1010 ，但是小数呢？ 有的小数无法用二进制表示。
例如，十进制的0.5表示为二进制是 0.1， 但是十进制的0.2表示为二进制会出现一个无限循环的小数：0.001100110011....
这是计算机无法完全处理小数的根本！
对于计算机处理浮点数的现状，暂时是无法改变的。它会带来一些误差，某些时候可能会因为一些不当的操作或者数据量的增加，而导致误差过大，但是这也只能通过我们的算法和设计来减轻。
最后，小数在内存中肯定不是以“0.25”这样带小数点的形式表示的，因为它必须转换成为二进制。书中提到了表示浮点数的IEEE745标准，也简单介绍了如何将一个浮点小数表示为二进制串，但这不是我学习的重点。因为对于这一点，先了解就好，有必要时再去深入研究。
-----------------------------------------------------------------------------------------
顺便，推荐一下我录制的《asp.net petshop4.0源码解读》教程，免费学习！
-----------------------------------------------------------------------------------------
总结一下：
前文提到的文字编码和数字，让我想起了上一篇讲过的一个词——数据抽象化。
计算机本来只能识别二进制码，通过这些年来的演变，使得它可以很友好的处理我们的语言和数学知识，这怎能不叫数据抽象呢。
再说个详细的例子，我们现在能通过打印机几秒钟打印一页文字，并轻松阅读，但是一开始要阅读计算机的语言，是打印纸带，再翻译纸带。大家可以试着通过ASCII码翻译一下这几个字母：
