看MIT的线性代数

长假期间，开始学组合图论，于是顺便把线性代数温习下，先是在verycd上看到有MIT Gilbert Strang教授的课程 ，然后搞来iTunes开始看，发现国外的老师讲课就是不一样——能够把我们认为一些“简单套公式”就能摆平的东西当作一个研究性课题讲上一大节课！小题大做了！但是，做过研究生的都知道，那些所谓的牛B人物，那些经典的论文，哪一个不是用类似的方式论述出来的？这样一个课堂上的问题的论述讲解，跟论文、演讲里的有什么不同？！学习和研究，本来就是一回事。如果你非要走捷径，最终还是要还的，在后续研究阶段要花上成倍的时间来弥补先前理论学习阶段理解的不够深入带来的遗憾。

 

Gilbert讲课还是有点不够熟练，说话甚至会卡壳、说话哆嗦，不过想起来原来的算法老师也是如此，恐怕是因为他们总想着把自己独特的理解呈现给学生，反而不如平铺直叙那样容易表达出来罢了。这样的一种思维方式，或许本来就是难于用普通直白的语言表达的，只可意会，不可言传。

Gilbert确实有独特之处——我之前从未听说过矩阵乘法还可以这么理解：向量的组合，解析几何的矢量和，前乘就是行向量的组合，后乘就是列向量的组合，矩阵相乘不是按结果矩阵元素位置挨个求解，而是看作行向量或列向量的加权组合，整体求解……我联想了很多，比如并行计算，分块计算，优化，matlab的矩阵运算库的实现

 

    ——哦天哪，Gilbert该不是就是Mathworks公司的科学家？？怎么这么熟悉，这么喜欢用matlab的内部原理来讲解这些运算过程？？

 

好吧，还是上正菜：

——————————————————————————

 

Lecture 1: The Geometry of Linear Equation

对于方程组的两种解释/理解：

1、Row picture。将未知数提取出来作为一个矩阵（列向量），将系数提取出来作为另一个矩阵（前乘阵），这样，方程组可以写成Ax=b，那么其中的每一个方程代表几何空间的一个对象集合f(x,y,z,...)=b：直线、曲线、乃至平面等。那么方程组的解，同时满足的这些方程的状态，就是几何对象的交集：交点、交线，乃至……？

2、Column picture。将未知数作为系数分配到系数阵（列向量），如[2 -1 ; -1 2][x; y] = [0; 3] 恒等于

[2 ; -1]x + [-1 ; 2]y = [0;3]，那么，方程组的左边可以看作是几何空间向量[2 ; -1]和向量[-1 ;2]的（加权）和，方程组的右边也可以看作另一个向量，而未知数就是这些向量的（伸缩）系数，方程组的解就是满足向量和的系数组合。

 

 

 

Lecture 2: Elimination with matrices

 

矩阵操作可以用矩阵乘法来实现。先说矩阵乘法：

1、后乘列向量：看作是列向量每个分量（第i行元素）作为系数分配到矩阵对应列（第i列）后的组合（系数加权求和）。

2、前乘行向量：看作是行向量每个分量（第j列元素）作为系数分配到矩阵对应行（第j行）后的组合（加权和）。

关于矩阵操作——行变换的乘法解释：如-3r₁ +r₂ ，相当于前乘一个矩阵（依据前乘行向量的意义）：

类似的也有列变换的乘法实现。

 

求解方程组有两种方法：利用行列式（determinant）、利用矩阵消解过程

高斯消解法（消解elimination而不是降解reduction）——it's always good to ask how could  it fail? So at the same time, we will see how elimination decides  whether the matrices is a good one  or has a problem, the to complete  the answer ,there is obviously a step of back substuition. In fact, the idea of elimination is,  you would thought of it, right ?  I mean Gauss thought of it before we did it, but only because he was born earlier. It's a natural idea. er.... and died earlier, too.

 

插入

Lecture 4: Factorization into A=LU

 

---

 

 

以下面的方程组为例，

，其扩展argumented矩阵为：

完整的Gauss消解过程分别可以用如下的矩阵乘法过程实现：

1、化成上三角阵

对角线上元素称为pivot，逐行选取pivot，利用multiplier做行加减运算，将左边的元素消除掉：

依次消除x_1、 x₂ 、x₃ ：

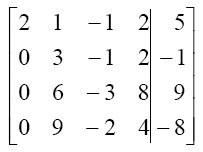  ---> ，记为U₁ ，记行变换用矩阵乘法描述为：E₁ = ，则U₁ =E₁ A

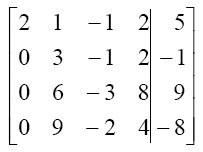--- >  ，记为U₂ ，记行变换所用前乘矩阵为：E₂ = ，则U₂ =E₂ U₁

 

 

--->  ，记为U，记行变换所用前乘矩阵为：E₃ = ，则U=E₃ U₂

 

 

 

消解过程可以用一系列下三角阵前乘来描述：U=E₃ U₂₌ E₃ E₂ U₁₌ E₃ E₂ E₁ A。

记L‘=E₁ E₂ E₃ ，则U=L’A。

记L'的逆矩阵为L，则LU=A。直观地说，L中的下三角元素就是上述消解时所用multiplier的相反数（加负号）。

这样，Gauss消解过程就可以看作是将A拆分为一个下三角阵L、与一个上三角阵U过程。

 

而之后的求解步骤也可以用L、U描述：LUx=b

（1）先解Lg=b。由于L是下三角阵，g向量可以由上而下解出。

（2）再解Ux=g。由于U是上三角阵，x向量可以由下而上解出。

 

考虑到pivot出现零值的情况，需要做行交换（换一个pivot非零的上来）。这种操作可以用Permutation矩阵描述：如下面的前乘矩阵P表示：第1行放的是原来的第3行、第2行放的是原来的第1行、第3行放的是原来的第4行、第4行放的是原来的2行。

 

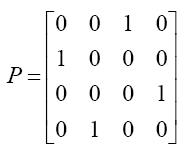
综上，整个Gauss消解过程可以用一系列下三角阵、置换阵前乘之来描述，U=E_n P_{n ...} E₂ P₂ E₁ P₁ A，

 

这样一种认识、一种描述方式，暗示了可以寻找其他简便方式来计算L、U，进而求解Ax=b。

对于 ，容易看出：

u_1,j = a_1,j   (用L的第1行乘上U的第j列)；

l_i,1 u_1,1 = a_i,1   (用L的第2，3，4行乘上U的第1列，取第一个元素)；

然后，缩小scope，迭代上述过程：

u_2,j = a_1,j - l_j,1 u_1,j

l_j,2 u_2,2 = a_i,1 - l_j,1 u_1,j

 

这种算法相对Gauss消解法的优势在于：

1、不涉及分支判断，便于采纳流水线执行技术；

2、除法次数减少（只有计算l的时候需要），舍入误差累积慢（除法位于二层循环，O(n² )，而Gauss中除法位于三层循环，为 O(n³ ) ）。

---

 

好了，用来求解方程组的Gauss消解法可以用一系列矩阵乘法来实现（E₁ E₂ ...A=U），进一步，可不可以将多步操作用到的矩阵E₁ E₂ 压成一个E？（ EA=U）。貌似比较困难，矩阵乘法没什么别的东西了。换一个角度，从最终效果上看，EA=U，求E可以看作是求E的逆，即A=E^-1 U。

 

Lecture 3: Multiplication and Inverse Matrices

什么样的矩阵不存在逆矩阵？

1、求它的秩；

2、解方程判断：如果能找到一个非零的x满足Ax=O，那么若果真有A^-1 ，则有A^-1 Ax=Ix=O，-> x=O，矛盾。

 

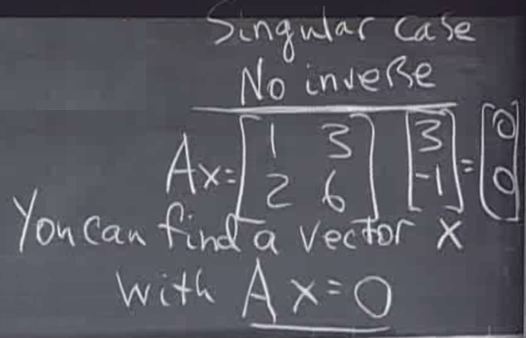
如果存在逆，如何求值？——Gauss-Jordan法：根据矩阵操作与矩阵乘法的对应关系，A^-1 A=I，意味着A^-1 是实现A的行向量某种操作（最终变换为I）的矩阵E。这种行操作可以复制、可以转移到另一个矩阵上 ，比如I，那么EI=A^-1 ，I变换后得到的矩阵就是A^-1 。这样一种方法可以这样操作：将A、I拼做一个矩阵[A|I]，然后将A变换为I，所用的操作同时施加到I上 ，这样最终得到[I|EI]，这个EI就是A^-1 。