Nvidia 的快速反量化操作
本文地址:https://wanger-sjtu.github.io/fast-dequant/
主要记录了论文Who Says Elephants Can't Run: Bringing Large Scale MoE Models into Cloud Scale Production中关于反量化的快速操作。
背景
NN模型通常为了降低RAM、FLASH占用,提高计算吞吐率,会引入量化操作。比如INT8、INT4、INT3等等。如果是weight only的量化方法情况,输入的部分还是浮点,在GPU、NPU、arm上float16用的比较多。这样一来,就需要在计算的时候,需要把权重反量化到浮点再进行计算。
论文在实验中发现,使用原生的native Int8ToFloat16做数值类型转换,性能并不符合预期。于是决定,将native Int8ToFloat16(吞吐低,底层应该是走 PTX cvt指令->SASS,关于ARM上计算,这里回头查一下)替换成一系列高吞吐的ALU和FP16运算指令,来巧妙地完成Int8->Float16的数值转换。
INT8 -> Float16
- 【观察一】 对于任意 FP16 数 X,其中 1024 ≤ X <2048, 1024 将准确地表示在指数位,而 int(X − 1024) 部分将直接存储在尾数中(二进制level原封不动地存储)。
- 【观察二】对于任何整数 0 ≤ Y < 1024,我们可以构造 Y + 1024 的 FP16 表示,将指数设置为 1024 并存储 Y在 FP16 尾数中。
首先,回忆一下浮点的表示方法。下图表示了float32的表示。
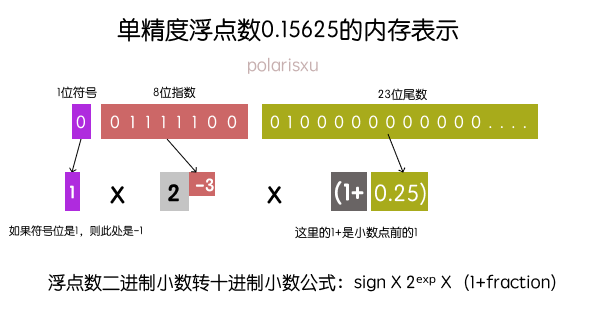
很明显可以看出来,右侧尾数表示的范围与左侧指数的表示范围是强相关的,左边指数范围越小,那么精度越高;反之,指数越大,精度越低。下面我们看下float16。
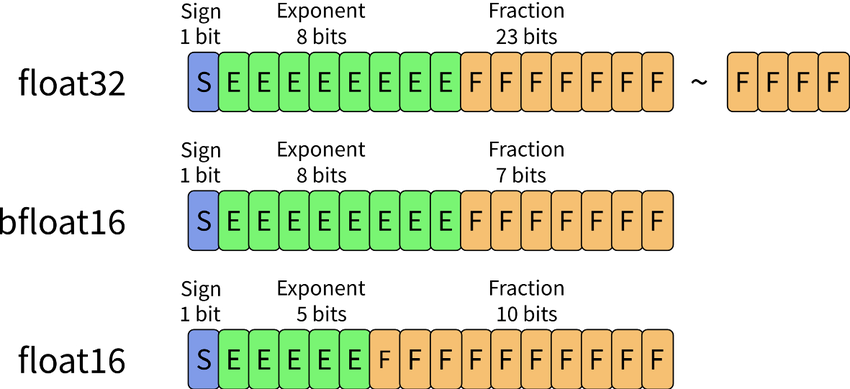
我们先忽略符号位部分,中间5bit表示指数,右边10bit表示小数。回到转10进制的表示,
其中fraction表示尾数部分的10进制数值,公式中之所以是(fraction/1024),是因为FP16尾数部分是10位,而2^10=1024。
来看一个FP16二进制转实数的列子,比如0b0110010000000011这个FP16,其中组成为:
0b 0 11001 0000000011
# 符号位:0
# 指数位:11001 -> 25 -> 25 - 15 = 10, 2^10=1024
# 尾数部分:0000000011 -> fraction为3(尾数部分的10进制数值)
转换为实数表达为:
1 * 2^10 * (1 + 3/1024) = 1027 = 1024 + 3 <-> 2^10 * 1 + 2^10 * 3/1024
观察一,是针对FP16数值而言的,它描述的其实是,FP16中落在\([1024, 2048)\) 范围中的数值,在16个bit位上的分布规律。如果转float32。同样道理算一下就可以。
现在从观察一可以得到一个结论:
\([1024, 2048)\) 范围内的float16整数x,在尾数部分的值恰好等于 x-1024
现在结合观察二,就得到量化后int4数值速转float16方法。
x = 0x6400 | (x &0b1111)
x = x - 1024
上面可以看出,这个操作仅支持正数,那么int8是有符号的怎么处理的呢?
量化存储的int值是加上了128转为u8,在反量化时需要减去这个128即可
参考链接:


