数据分析-numpy的用法
一、jupyter notebook
两种安装和启动的方式:
第一种方式:
命令行安装:pip install jupyter
启动:cmd 中输入 jupyter notebook
缺点:必须手动去安装数据分析包(比如numpy,pandas...)
第二种方式:
下载anaconda软件
优点:包含了数据分析的基础包大概200个左右的科学运算包
jupyter notebook一些快捷键操作:
1. 运行当前代码并选中下一个单元格 shift+enter 2. 运行当前的单元格 crtl + enter 绿色: 编辑模式 蓝色: 命令行模式 3. 在单元格的上方添加一个单元格 , 按esc进入命令行模式,接下来按 a (above) 添加 4. 在单元格的上方添加一个单元格 , 按esc进入命令行模式,接下来按 b (below) 添加 5. 删除一个单元格, 按esc进入命令行模式, 接下来,按 dd(delete) 删除 6. 代码和markdown的切换, 按esc进入命令行模式, 接下来,按 m 切换
二、numpy的用法
导入方式: import numpy as np
1.ndarray-多维数组对象
创建ndarray对象
np.array()
2.ndarray是一个多维数组列表
一维
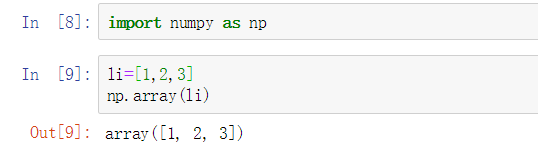
二维 (被几层中括号包围,就是几维,里面的都是一层) 多维就是以此类推

注意:数组和python中的列表很像,但是它们之间有什么区别呢?(******)
1.数组对象内的元素类型必须相同
2.数组大小不可修改
3.常用的属性(******)

属性T (数组的转置,下面的例子。原来是二维数组 两行三列,转置之后变成三行两列)
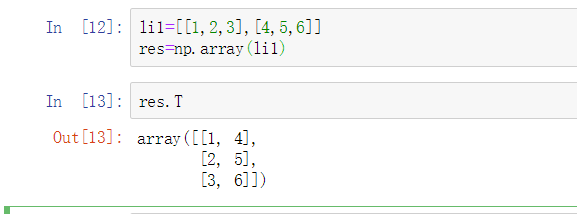
属性dtype (获取数据的类型)
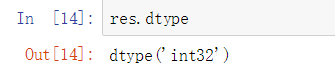
属性size (数组元素的个数)

属性ndim (数组的维度)
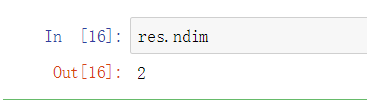
属性shape (以元组形式) 两行三列
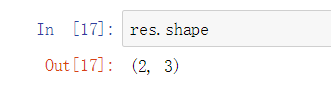
4.数据类型 dtype(******)

整型: int32只能表示(-2**31,2**31-1),因为它只有32个位,只能表示2**32个数 无符号整型: 只能用来存正数,不能用来存负数 补充: astype()方法可以修改数组的数据类型
astype()方法

5.创建ndarray方式(******)
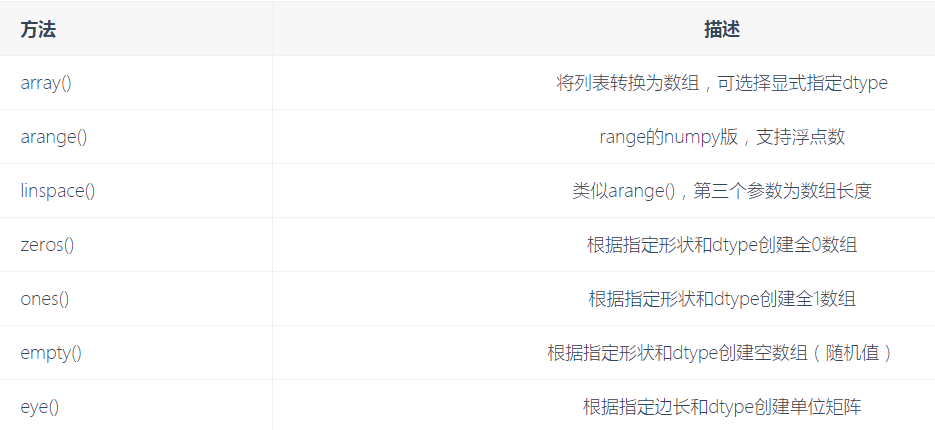
arange() 类似于python的range版本 可以设置起始值和终止值,还有步长

linspance() 这个和arange不一样,这个是顾头也顾尾。前两个参数是设置取值区间,第三个参数在这个区间均等取几份

zeros() 用0组成一个多维数组
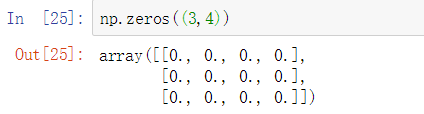
ones() 用1组成一个多维数组
empty() 随机指定维度的数组,数字是随机的

eye() 指定维度创建单位矩阵,对角是1
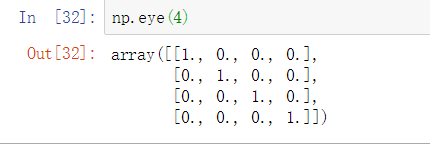
6.索引和切片(******)
数组和标量(数字)之间的运算
li1 = [ [1,2,3], [4,5,6] ] a = np.array(li1) a * 2 运行结果: array([[ 2, 4, 6], [ 8, 10, 12]])
同样大小数组之间的运算
# l2数组 l2 = [ [1,2,3], [4,5,6] ] a = np.array(l2) # l3数组 l3 = [ [7,8,9], [10,11,12] ] b = np.array(l3) a + b # 计算 执行结果: array([[ 8, 10, 12], [14, 16, 18]])
索引
# 将一维数组变成二维数组 arr = np.arange(30).reshape(5,6) # 生成五行六列的二维数组# 将二维变一维 arr.reshape(30) # 索引使用方法 array([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11], [12, 13, 14, 15, 16, 17], [18, 19, 20, 21, 22, 23], [24, 25, 26, 27, 28, 29]]) 现在有这样一组数据,需求:找到20
#两种写法 列表写法:arr[3][2] 数组写法:arr[3,2] # 中间通过逗号隔开就可以了,逗号前面的是行索引,后面的是列索引,都是从0开始
切片
arr数组 array([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11], [12, 13, 14, 15, 16, 17], [18, 19, 20, 21, 22, 23], [24, 25, 26, 27, 28, 29]]) arr[1:4,1:4] # 切片方式
#逗号前面是行索引 1:4代表 第2行到第4行,后面是列索引 1:4代表 第2列到第4列
执行结果: array([[ 7, 8, 9], [13, 14, 15], [19, 20, 21]])
注意:最后会发现修改切片后的数据影响的依然是原数据。有的人可能对一点机制有一些不理解的地方,像Python中内置的都有赋值的机制,而Numpy去没有,其实是因为NumPy的设计目的是处理大数据,所以你可以想象一下,假如NumPy坚持要将数据复制来复制去的话会产生何等的性能和内存问题。
总结:索引和切片和python原生的列表切片,索引相似。需要注意高维数组的索引和切片中逗号的使用。
布尔型索引(******)
需求:现在有一个数组,需要取出大于5的数。
li = [random.randint(1,10) for _ in range(30)] #生成在1到9中随机挑选的30个整数,组成一维数组 a = np.array(li) a[a>5] 执行结果: array([10, 7, 7, 9, 7, 9, 10, 9, 6, 8, 7, 6]) ---------------------------------------------- 原理: a>5会对a中的每一个元素进行判断,返回一个布尔数组 a > 5的运行结果: array([False, True, False, True, True, False, True, False, False, False, False, False, False, False, False, True, False, True, False, False, True, True, True, True, True, False, False, False, False, True]) ---------------------------------------------- 布尔型索引:将同样大小的布尔数组传进索引,会返回一个有True对应位置的元素的数组(******)
花式索引(******)
res = np.array([1,2,3,4,5,6,7,8,9,10]) 现在有一个这样的数组,需要获取值2,4,7,9 res[[1,3,6,8]] #内层括号中的数字指的是想要获取的值的索引下标
三、numpy中通用函数
能对数组中所有元素同时进行运算的函数就是通用函数
常见通用函数:
能够接受一个数组的叫做一元函数,接受两个数组的叫二元函数,结果返回的也是一个数组
一元函数:
| 函数 | 功能 | |
|---|---|---|
| abs、fabs | 分别是计算整数和浮点数的绝对值 | |
| sqrt | 计算各元素的平方根 | |
| square | 计算各元素的平方 | |
| exp | 计算各元素的指数e**x | |
| log | 计算自然对数 | |
| sign | 计算各元素的正负号 | |
| ceil | 计算各元素的ceiling值,向上取整 | |
| floor | 计算各元素floor值,向下取整 | |
| rint | 计算各元素的值四舍五入到最接近的整数,保留dtype | |
| modf | 将数组的小数部分和整数部分以两个独立数组的形式返回,与Python的divmod方法类似 | |
| isnan | 判断各元素是否NaN(类似于空),非NaN返回False | |
| isinf | 表示那些元素是无穷的布尔型数组 | |
| cos,sin,tan | 普通型和双曲型三角函数 |
abs (整数绝对值)
np.abs(-2) #2
np.abs([-2,-4,-5,-10]) #array([2,4,5,10])
fabs (浮点型绝对值)
np.fabs([-1.3,-2.5,-3.4]) #array([1.3,2.5,3.4])
sqrt (元素的平方根)
np.sqrt(4) #2.0
square() (求平方)
np.square(2) #4
sign (取某个数的符号)
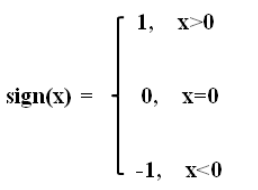
np.sign([-0.2, -1.1, 0, 2.3, 4.5, 0.0]) #array([-1., -1., 0., 1., 1., 0.])
modf (小数部分和整数部分以两个独立数组的形式返回)
np.modf([1.3,2.5]) #(array([0.3, 0.5]), array([1., 2.]))
isnan (判断是否为NaN)
np.isnan(10) #False np.isnan(np.nan) #True
二元函数:
| 函数 | 功能 | |
|---|---|---|
| add | 将数组中对应的元素相加 | |
| subtract | 从第一个数组中减去第二个数组中的元素 | |
| multiply | 数组元素相乘 | |
| divide、floor_divide | 除法或向下圆整除法(舍弃余数) | |
| power | 对第一个数组中的元素A,根据第二个数组中的相应元素B计算A**B | |
| maximum,fmax | 计算最大值,fmax忽略NAN | |
| miximum,fmix | 计算最小值,fmin忽略NAN | |
| mod | 元素的求模计算(除法的余数) |
数学统计方法:
| 函数 | 功能 | |
|---|---|---|
| sum | 求和(注意可以加参数使用) | |
| cumsum | 求前缀和 | |
| mean | 求平均数 | |
| std | 求标准差 | |
| var | 求方差 | |
| min | 求最小值 | |
| max | 求最大值 | |
| argmin | 求最小值索引 | |
| argmax | 求最大值索引 |
cumsum (1,1+2,1+2+3,依次这样加上求出结果)
np.cumsum([[1,2,3], [4,5,6]]) #array([ 1, 3, 6, 10, 15, 21], dtype=int32)
max (求出元素最大值)
np.max([2,5,3,9]) #9
argmax (获得元素最大值的索引)
np.argmax([2,5,8,9]) #3
随机数
随机生成函数在np.random的子包当中
| 函数 | 功能 | |
|---|---|---|
| rand | 给定形状产生随机数组(0到1之间的数) | |
| randint | 给定形状产生随机整数 | |
| chocie | 给定形状产生随机选择 | |
| shuffle | 与random.shuffle相同,随机排序 | |
| uniform | 给定形状产生随机数组 |
rand (生成一个0-1之间的随机数)
np.random.rand() #0.49166803964675165
randint (随机生成一个整数)
np.random.randint(1,10) #3
choice (在0-2中随机生成3个数)
np.random.choice(3,3) #array([0, 2, 1])
uniform (在给定数据中随机产生数组)
np.random.uniform(-1,0,20) #结果 array([-0.66594843, -0.5310402 , -0.29780177, -0.07202016, -0.28427749, -0.56300027, -0.77879767, -0.16601984, -0.28470704, -0.95631047, -0.37167632, -0.88102119, -0.33952064, -0.94433562, -0.49175838, -0.47084326, -0.96345379, -0.70347248, -0.85644044, -0.46857343])
当你不知道此方法有什么参数值,你可以在后面加一个问号,然后按shfit+enter,下面就会跳出解释





