（ECCV2024论文解读，三维点云理解）GPSFormer: A Global Perception and Local Structure Fitting-based Transformer for Point Cloud Understanding

目录

• 摘要
• 1、引言
• 2、方法
  • 2.1 背景
  • 3.2 全局感知模块
  • 2.3 局部结构拟合卷积
    • 泰勒级数
    • 局部结构拟合卷积
    • 显式结构引入
  • 2.4 GPSFormer
    • 点云分类
    • 部件分割任务
• 3、实验
  • 3.1 3D形状分类
    • ScanObjectNN数据集上的形状分类
    • ModelNet40数据集上的形状分类
  • 3.2 部件分割
  • 3.3 小样本分类
  • 3.4 消融研究
    • 全局感知模块的有效性
    • ADGConv的邻域大小
    • 高阶卷积的参数影响
  • 3.5 可视化
  • 3.6 模型复杂度
• 4、总结

GPSFormer: A Global Perception and Local Structure Fitting-based Transformer for Point Cloud Understanding
GPSFormer：一种基于全局感知和局部结构拟合的点云理解Transformer

Changshuo Wang[1], Meiqing Wu[1], Siew-Kei Lam[1,2], Xin Ning[3], Shangshu Yu[1], Ruiping Wang[1], Weijun Li[3],Thambipillai Srikanthan[1,2] [1]Cyber Security Research Center (CYSREN), Nanyang Technological University [2]College of Computing and Data Science, Nanyang Technological University [3]Institute of Semiconductors, Chinese Academy of Sciences

论文地址：https://arxiv.org/abs/2407.13519v1
代码：https://github.com/changshuowang/GPSFormer

摘要

  尽管点云理解的预训练方法取得了显著进展,但直接从不规则点云中捕捉复杂的形状信息而不依赖外部数据仍然是一个巨大的挑战。为了解决这个问题,我们提出了GPSFormer,这是一种创新的基于全局感知和局部结构拟合的Transformer,能够以卓越的精度从点云中学习详细的形状信息。GPSFormer的核心是全局感知模块(GPM)和局部结构拟合卷积(LSFConv)。具体来说,GPM利用自适应可变形图卷积(ADGConv)来识别特征空间中相似特征之间的短程依赖关系,并采用多头注意力(MHA)来学习特征空间中所有位置之间的长程依赖关系,最终实现灵活学习上下文表示。受泰勒级数启发,我们设计了LSFConv,它从显式编码的局部几何结构中学习低阶基本信息和高阶细节信息。将GPM和LSFConv作为基本组件,我们构建了GPSFormer,这是一种能有效捕捉点云全局和局部结构的前沿Transformer。大量实验验证了GPSFormer在三个点云任务中的有效性:形状分类、部件分割和小样本学习。GPSFormer的代码可在https://github.com/changshuowang/GPSFormer获取。

1、引言

  近年来,点云理解技术已广泛应用于自动驾驶、机器人和公共安全等领域。然而,由于点云的无序和不规则性质,有效地从中提取固有的形状信息仍然是一个极具挑战性的研究课题。准确高效地从点云中学习形状感知已成为一个突出且值得关注的问题。

  早期研究将点云数据转换为多视图或体素表示,利用传统卷积神经网络学习形状信息。然而,这种转换过程常常导致固有几何信息的丢失,并且计算成本高昂。PointNet直接独立编码点云中的每个点,并通过最大池化聚合全局特征,但这种方法忽视了局部结构信息。为了解决这个问题,后续工作提出了一系列基于局部特征聚合的方法。这些方法通过最远点采样(FPS)将点云划分为不同的局部子集,然后通过构建局部聚合算子学习局部形状表示,最后通过构建层次结构从局部到全局学习形状感知。然而,这些方法忽视了点之间的长程依赖关系。

  一些研究者利用Transformer强大的长程依赖学习能力,并将这种结构应用于点云分析。例如,Point Transformer使用局部邻域中的自注意力来学习点之间的长程依赖关系。PCT提出了一个偏移注意力模块来学习全局上下文表示。然而,同时考虑短程依赖关系和长程依赖关系以及局部结构建模的Transformer很少被探索。随着自监督学习和大型语言模型的快速发展,一些研究者提出了一系列基于预训练或多模态大型语言模型的方法。尽管这些方法通过利用外部数据来辅助点云模型提高了性能,但它们并没有完全解决点云结构表示的问题。

  为了克服这些限制,我们提出了GPSFormer来从点云中学习丰富的上下文形状感知。GPSFormer由两个核心组件组成:全局感知模块(GPM)和局部结构拟合卷积(LSFConv)。在GPM中,我们引入了自适应可变形图卷积(ADGConv),使点特征能够动态地浏览整个点云特征空间。这允许灵活构建合适的局部邻域,促进相似结构的强特征表示和短程依赖关系的学习。随后,转换前后的特征都被输入到残差交叉注意力(RCA)中,丰富了上下文结构理解。最后,模型利用多头注意力(MHA)来捕捉点云中固有的长程依赖关系。受泰勒级数启发,我们设计了LSFConv,将局部结构表示视为多项式拟合问题,以精确捕捉局部几何信息的微妙变化。具体来说,低阶项用于拟合局部结构的平坦部分,通常包括点云的基本形状和整体趋势。高阶项用于拟合局部结构的边缘和细节部分,从而捕捉复杂变化和精细特征。如图1所示,GPSFormer达到了优异的性能。

  

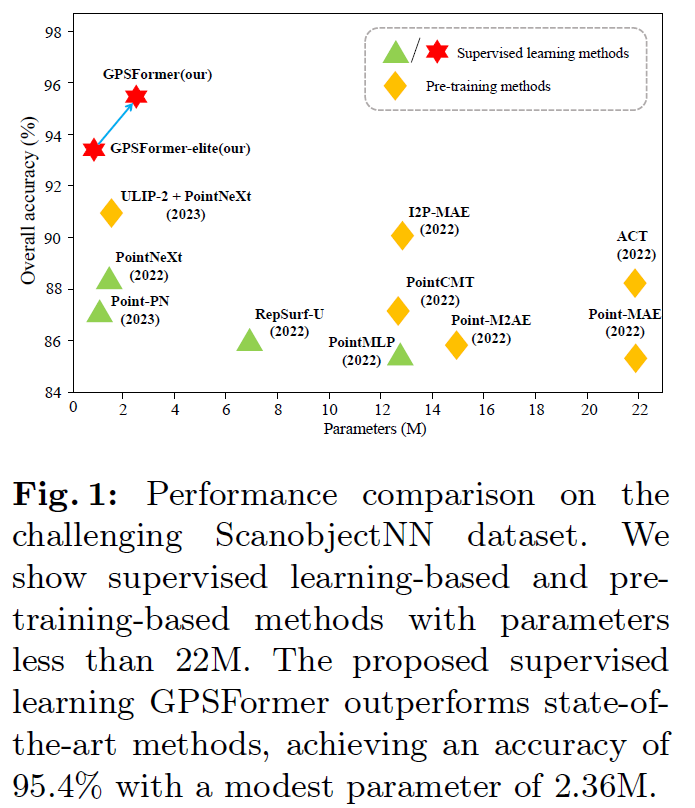
  本文的主要贡献有三个方面：

(1）提出了GPSFormer,一种基于全局感知和局部结构拟合的transformer,用于从不规则点云中学习丰富的上下文信息和精确的形状感知。

(2）引入了新颖的GPM和LSFConv。GPM学习点的短程和长程依赖关系,而受泰勒级数启发的LSFConv通过多项式拟合捕捉低频和高频局部几何信息。

(3）所提出的GPSFormer在三个点云任务中达到了最先进的结果,特别是在具有挑战性的ScanObjectNN数据集上的准确率比当前最佳的监督学习方法高出5.0%。

2、方法

  如图3所示,详细阐述了所提出的GPSFormer。本节结构如下:首先,回顾点卷积(第2.1节)。其次,介绍全局感知模块(GPM)(第2.2节)。第三,提出局部结构拟合卷积(LSFConv)(第2.3节)。第四,基于GPM和LSFConv,介绍GPSFormer架构及其应用细节(第2.4节)。

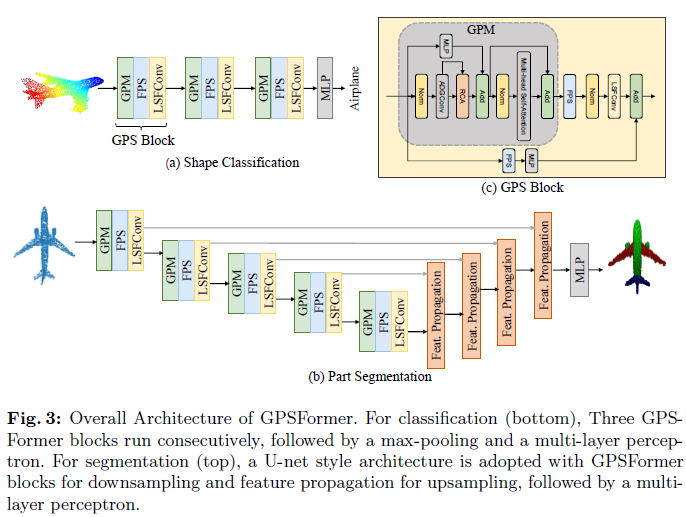
2.1 背景

  当前基于局部特征聚合的方法通常遵循"采样-分组-聚合"的结构设计来构建局部特征提取块。采样操作利用最远点采样(FPS)方法对输入点云进行下采样,创建一组具有代表性的采样点。分组操作通常采用K近邻(KNN)或球形查询为每个具有代表性的采样点构建局部邻域。聚合步骤使用映射函数和最大池化来获得局部形状表示。

  对于每个阶段,我们假设具有代表性的采样点可以描述为\(\{(p_i, f_i)\}_{i=1}^M\),其中\(M\)表示点的数量,\(p_i \in \mathbb{R}^{1 \times 3}\)和\(f_i \in \mathbb{R}^{1 \times C}\)分别表示第\(i\)个点的坐标和特征。\(C\)表示特征通道的数量。局部特征聚合的点卷积可以形式化为:

\[f_i^{\prime}=\mathcal{A}\left(\left\{\mathcal{M}\left(p_i, p_j\right) \cdot \mathcal{T}\left(f_i, f_j\right) \mid p_j \in \mathcal{N}\left(p_i\right)\right\}\right), \]

其中\(\mathcal{A}\)是聚合函数,通常是最大池化。\(\mathcal{M}\)和\(\mathcal{T}\)是映射函数,通常通过多层感知器(MLPs)实现。\(N(p_i)\)表示\(p_i\)的局部邻域,\(p_j\)是\(p_i\)的邻近点。

  另一种聚合方法是在特征空间中进行聚合,通常称为动态图卷积(DGC)。它在特征空间中聚合局部特征,这意味着在特征空间中接近的点在坐标空间中可能相距较远。DGC可以形式化为:

\[f_i^{\prime}=\mathcal{A}\left(\left\{\mathcal{T}\left(f_i, f_j\right) \mid f_j \in \mathcal{N}\left(f_i\right)\right\}\right). \]

3.2 全局感知模块

  直接聚合点云的局部特征可能难以捕获有意义的形状信息。我们发现,在局部特征聚合之前对点特征进行全局上下文建模有助于获得稳健的形状感知。因此,我们开发了全局感知模块(GPM),该模块首先采用创新的自适应可变形图卷积(ADGConv)来增强特征空间中相似特征之间的短程依赖关系。随后,它利用残差交叉注意力(RCA)和多头注意力(MHA)来捕获特征空间中所有位置之间的长程依赖关系。GPM为后续的局部结构拟合提供指导。

  首先,动态图通常使用KNN在特征空间中构建,这使得动态图的接受域容易受到邻近点数\(K\)的影响。当K较小时,动态图的接受域集中在局部坐标邻域。当\(K\)较大时,动态图的接受域分布在一些语义上不相关的点上,这使得难以在相似组件内学习可区分的特征表示。

  为了解决这个问题,我们引入了ADGConv。初始时,我们为采样点定义一个特征偏移\(\Delta(f_i)\),允许它们遍历整个特征空间并灵活构建适当的局部邻域。偏移\(\Delta(f_i)\)通过可学习的特征变换函数\(\phi\)为具有代表性的采样点\(f_i\)自适应获得,表示\(f_i\)对特征空间中特定位置的偏好。变换后的特征\(\hat{f}_i\)可以通过\(f_i\)和\(\Delta(f_i)\)获得。我们使用\(\hat{f}_i\)作为中心点,以原始特征\(f_i\)定义采样空间来构建局部邻域,以构建动态图以获得增强特征\(f_i^d\)。ADGConv的这种漫游过程有助于在相似组件之间学习稳健的特征表示。ADGConv可以形式化如下:

\[\Delta\left(f_i\right)=\phi\left(f_i\right), \]

\[\hat{f}_i=f_i+\Delta\left(f_i\right) \]

\[\mathcal{T}\left(\left(\hat{f}_i\right), f_j\right)=\psi\left(\left[\hat{f}_i, f_j-\hat{f}_i\right]\right) \]

\[f_i^a=\mathcal{A}\left(\left\{\mathcal{T}\left(\widehat{f}_i, f_j\right) \mid f_j \in \mathcal{N}\left(\widehat{f}_i\right)\right\}\right) \]

其中\(\phi\) 和 \(\psi\)表示MLPs,\([\cdot]\)表示连接。\(f_i^a \in \mathbb{R}^{1 \times C}\)是ADGConv的输出。

  接下来,RCA通过交叉注意力融合位移特征\(\hat{f}_i\)和ADGConv的输出特征$ f_i^a $,公式为:

\[f_i^r = f_i^a + \text{Attn}(\hat{f}_i, f_i^a, f_i^a). \]

  最后,RCA的输出$ f_i^r $然后被输入到MHA中,以进一步学习特征空间中所有位置之间的长程依赖关系,增强模型对点云特征的表示能力。MHA可以形式化如下:

\[f_i^g = \text{Attn}(Q_i, K, V) = \text{Softmax}\left(\frac{Q_i K^T}{\sqrt{h}}\right) V, \]

其中\(Q_i = Z \hat{W}^Q\), \(K = Z\hat{W}^K\), 和 \(V = Z\hat{W}^V\)。\(\hat{W}^Q \in \mathbb{R}^{C \times C_h}\), \(\hat{W}^K \in \mathbb{R}^{C \times C_h}\), 和\(\hat{W}^V \in \mathbb{R}^{C \times C_h}\)表示线性映射矩阵。\(Z = \{f_i^r\}_{i=1}^M\)表示RCA的输出矩阵。

2.3 局部结构拟合卷积

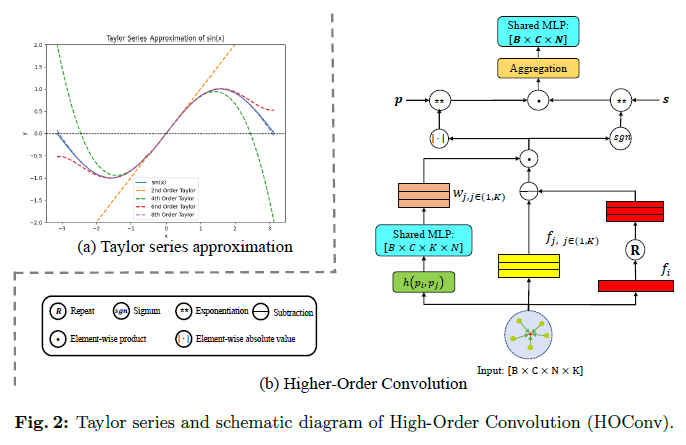
泰勒级数

  受泰勒级数启发(见图2(a)),在GPM的基础上,我们采用局部拟合方法来更细致地分析点云的局部结构和细节。泰勒级数由以下公式给出:

\[f(x) = f(a) + \sum_{n=1}^{\infty} \frac{f^{(n)}(a)}{n!}(x - a)^n, \quad |x - a| < \epsilon , \]

其中\(a\)是一个常数,\(\epsilon\)是一个无穷小量。为简化计算,我们将泰勒级数分解为低频分量和高频分量,表示为:

\[f(x) \approx f(a) + \sum_{n=1}^{\infty} a_n (x - a)^n, \quad |x - a| < \epsilon, \]

其中\(a_n = \frac{f^{(n)}(a)}{n!}\)。基于等式(10),可以理解为,在点云局部结构的表示中,低频分量\(f(a)\)表示局部结构的平坦部分和点云的整体趋势,而高频分量\(\sum_{n=1}^{\infty} a_n (x - a)^n\)表示局部结构的边缘和细节部分。

局部结构拟合卷积

  受泰勒级数启发,我们学习嵌入在局部结构中的整体信息(低频信息)\(f_i^L\)和细化细节(高频信息)\(f_i^H\)。因此,提出的LSFConv由以下给出:

\[f(\{f_j\}_{j=1}^K) \approx f_i^L + f_i^H = \mathcal{A}(\{\phi(f_j)\}_{j=1}^K) + \mathcal{A}(\{\mathcal{T}(f_i, f_j)\}_{j=1}^K), \]

\[\mathcal{T}\left(f_i, f_j\right)=\left(\frac{w_j \cdot\left(f_j-f_i\right)}{\left|w_j \cdot\left(f_j-f_i\right)\right|}\right)^s \cdot\left|w_j \cdot\left(f_j-f_i\right)\right|^p, \]

其中我们将\(f_i^L\)称为低阶卷积(LOConv),\(f_i^H\)称为高阶卷积(HOConv,见图2(b))。\(\phi\)表示MLP。\(\mathcal{T}(f_i, f_j)\)是一种新颖的仿射基函数。这里,\(|\cdot|\)表示元素级绝对值,\(s \in \{0,1\}\),\(p\)是可学习参数。当\(s=1, p=1\), \(\mathcal{T}(f_i, f_j)\)时,\(\mathcal{T}(f_i, f_j)\)退化为仿射基函数(ABF);当\(s=0, p=2\)时,\(\mathcal{T}(f_i, f_j)\)退化为径向基函数(RBF)。因此,提出的\(\mathcal{T}\) 展现了强大的表示能力。

\[\mathcal{T}=\left(\frac{w_j \cdot\left(f_j-0\right)}{\left|w_j \cdot\left(f_j-0\right)\right|}\right)^1 \cdot\left|w_j \cdot\left(f_j-0\right)\right|^1=w_j \cdot f_j \]

\[\mathcal{T}=\left(\frac{w_j \cdot\left(f_j-f_i\right)}{\left|w_j \cdot\left(f_j-f_i\right)\right|}\right)^0 \cdot\left|w_j \cdot\left(f_j-f_i\right)\right|^2 \]

显式结构引入

  点云中采样点和邻近点之间的交互可以明确反映局部点云的相关性。如果我们能利用这种先验知识来学习权重\(w_j\),它将显著增强局部结构拟合卷积感知点云局部形状的能力。我们将采样点\(p_j\)和邻近点\(p_{i j}\)
之间的交互表示为:

\[h\left(p_i, p_{i j}\right)=\left[p_i, p_j, p_j-p_i,\left\||p_i, p_j\right\||\right], \]

其中\(||\cdot||\)表示计算欧几里得距离。因此,\(w_j\)定义为:

\[w_j = \xi(h(p_i, p_j)), \]

其中\(\xi\)表示MLP。
  显式引入几何信息有利于局部拟合卷积学习点之间的相对空间布局关系,并捕获局部几何特征和详细信息。

2.4 GPSFormer

  如图3所示,基于全局感知模块(GPM)和局部结构拟合卷积(LSFConv),我们设计了一个基于Transformer架构的模型,称为GPSFormer,用于点云分析。

点云分类

  对于点云分类任务,我们通过级联GPS块构建了一个堆叠的GPSFormer。在每个GPS块中,首先使用GPM进行全局感知。随后,通过FPS获得具有代表性的采样点。最后,在每个采样点周围构建局部邻域,并通过提出的LSFConv实现局部形状感知。

  我们为点云分类采用三个阶段的GPS块,每个阶段的特征维度设置为\({64, 128, 256}\)。同时,我们还评估了一个紧凑变体,称为GPSFormer-elite,每个阶段的特征维度输出设置为\({32, 64, 128}\)。通过最大池化和多层感知器(MLP)对点云进行预测。在LSFConv的每个阶段,采用多尺度策略进行局部特征提取。利用球形查询构建具有多尺度半径\({0.1, 0.2, 0.4}\)的局部邻域,对应的邻域点数为\({8, 16, 32}\)。多尺度参数在各个阶段保持一致,从而避免了参数调整的麻烦。

部件分割任务

  对于部件分割,我们在编码器阶段使用五个阶段的GPS块。每个阶段构建局部邻域的方法和参数与分类任务相同。此外,采用具有反向插值算法的解码器来恢复点云的分辨率。在编码器和解码器之间,应用了类似U-Net的跳跃连接结构,充分利用上下文信息。

3、实验

3.1 3D形状分类

ScanObjectNN数据集上的形状分类

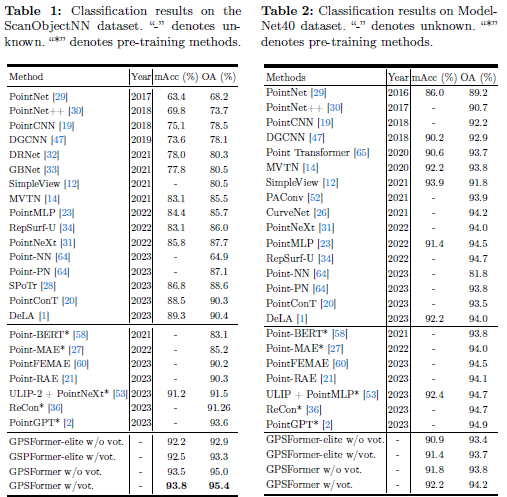
  ScanObjectNN是一个为点云分类收集的真实世界数据集。该数据集中的对象包括背景并考虑了遮挡,使其比ModelNet40更加真实和具有挑战性。该数据集包含2902个点云对象,分为15个对象类别,我们在其最具挑战性的扰动变体(PB_T50_RS)上进行了实验。
如表1所示,我们将比较方法分为纯监督学习和预训练方法。表1表明,所提出的GPSFormer在所有方法中表现最佳,mAcc和OA分别达到93.8%和95.4%。这一结果比预训练方法PointGPT的OA高1.8%,比纯监督方法DeLA的mAcc和OA分别高4.5%和5.0%。即使是紧凑型的GSPFormer-elite也仅用0.68M参数就达到了93.3%的OA。这一结果展示了GPSFormer捕获长程依赖关系和局部结构表示的强大能力。

ModelNet40数据集上的形状分类

  ModelNet40数据集被广泛认为是点云分析的基准,由代表复合对象的点云组成。它包含40个类别(如飞机、汽车、植物和灯),9843个样本用于训练,剩余的2468个用于测试。
  如表2所示,所提出的GPSFormer在合成ModelNet40数据集上实现了94.2%的令人印象深刻的准确率,优于大多数监督和预训练方法。这一结果突显了GPSFormer的有效性和泛化能力。目前,现有方法在较不具挑战性的合成ModelNet40数据集上基本达到饱和,这些先进方法之间的性能差距不到0.8%。然而,这种微小的差距掩盖了它们在真实世界数据集(如ScanObjectNN)上的相对较差表现。因此,ModelNet40数据集本身不能作为模型性能的准确评估基准。

3.2 部件分割

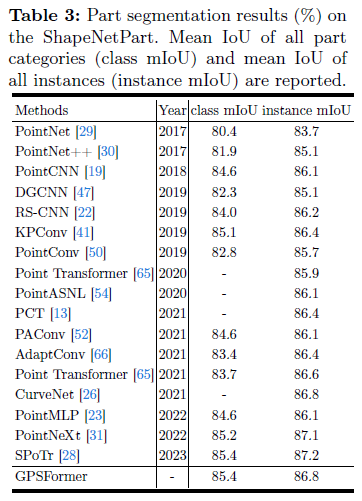
  ShapeNetPart是大规模3D CAD模板库ShapeNet的一个子集,包含16个常见对象类别(如桌子、椅子、飞机等)的16,881个形状。每个形状都标注了2-5个部件,总共有50个部件类别。在这个实验中,我们使用13,807个模型进行训练,2,874个模型进行测试。

  如表3所示,我们使用每个实例的平均IoU和类IoU评估了GPSFormer在部件分割上的性能。我们随机选择2048个点作为输入,并报告了10次投票后的结果。显然,与现有方法相比,GPSFomer取得了具有竞争力的结果,特别是在类IoU方面达到了85.4%的最佳性能。图4a显示了一些部件分割的结果,表明GPSFormer可以有效识别物体的形状信息并准确分割相似的组件。

3.3 小样本分类

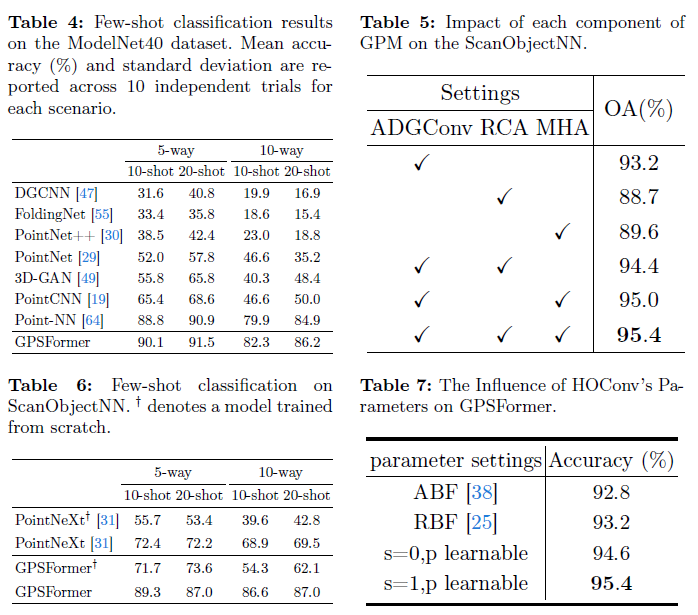
  现有方法在ModelNet40上进行小样本分类。为了更好地反映模型在复杂环境中的能力,我们按照ModelNet40的划分方法为ScanObjectNN提供了一个小样本数据集。根据之前工作的设置,我们采用了"n-way m-shot"设置,从数据集中随机选择n个类别,并从每个类别中随机选择m个样本进行训练。在测试时,从n个类别的剩余样本中随机选择20个样本。因此,我们在四种设置下进行评估(5-way 10-shot, 5-way 20-shot, 10-way 10-shot, 10-way 20-shot),每种设置进行10次独立实验,并使用实验结果的平均值作为模型的性能指标。表4和表6提供了GPSFormer在ModelNet40和ScanObjectNN上的小样本分类性能。可以看出,所提出的GPSFormer能够在有限样本中学习稳健的形状信息。

3.4 消融研究

全局感知模块的有效性

  如表5所示,很明显ADGConv、RCA和MHA模块在点云上下文建模中起着至关重要的作用。单独来看,ADGConv通过动态图卷积有效提取局部特征,达到93.2%的准确率。RCA贡献于全局关系,达到88.7%的准确率,而MHA捕获依赖关系,虽然效果不如ADGConv和RCA。结合ADGConv和RCA将准确率提高到94.4%,突显了它们的互补性。ADGConv和MHA的组合达到95.0%,验证了它们的有效性。最后,同时使用三个模块达到了最高的95.4%准确率,强调了它们在增强点云分析模型性能方面的协同作用。

ADGConv的邻域大小

  由于ADGConv在特征邻域内聚合特征,邻近点在空间位置上具有强烈的语义关系。如果邻域太小,将导致ADGConv在邻域内进行局部特征聚合;如果邻域太大,不仅会增加模型的搜索时间,还会引入一些不相关的点特征。如表8所示,当邻域大小为20时,模型可以学习良好的上下文信息。然而,当邻域太大或太小时,将无法学习到有价值的语义信息。

高阶卷积的参数影响

  如表7所示的结果,高阶卷积(HOConv)在塑造网络性能方面起着关键作用。可学习参数p和设置s = 1的配置表现最为有效,达到了95.4%的显著准确率。这突显了自适应参数调整在增强网络结果方面的重要性。尽管基线方法ABF和RBF分别记录了92.8%和93.2%的可观准确率,但自适应参数设置明显超过了它们。

3.5 可视化

图4b使用Point-Bert和GPSFormer可视化了ScanObjectNN数据集上样本特征的空间分布。可以看出,所提出的GPSFormer能够更好地减少对象的类内距离,使样本分布更加紧凑,有效识别对象的形状信息。

3.6 模型复杂度

  表9提供了GPSFormer在ScanObjectNN数据集上的模型复杂度评估。GPSFormer仅略微增加参数数量就在速度和准确性方面实现了最佳结果,仅具有2.36M参数和0.7G FLOPS。这突显了其在点云理解任务中的有效性和效率。

4、总结

  在本文中,我们提出了一种新颖的基于全局感知和局部结构拟合的Transformer(GPSFormer),以解决从不规则点云中有效捕获形状信息的挑战。GPSFormer的主要贡献包括引入全局感知模块(GPM)和局部结构拟合卷积(LSFConv)。GPM通过引入自适应可变形图卷积(ADGConv)增强了模型捕获点云全局上下文信息的能力。同时,LSFConv精细地学习点云的局部几何结构,获取低阶基本信息和高阶细节信息。通过在三个点云理解任务中进行广泛的实验,所提出的GPSFormer展示了在不依赖外部数据的情况下高效处理和分析点云的能力。在未来,我们计划进一步探索GPSFormer在预训练、轻量化方法和小样本学习设置中的潜力。