(论文笔记ICCV2021)Persistent Homology based Graph Convolution Network for Fine-grained 3D Shape Segmentation
论文地址：https://openaccess.thecvf.com/content/ICCV2021/html/Wong_Persistent_Homology_Based_Graph_Convolution_Network_for_Fine-Grained_3D_Shape_ICCV_2021_paper.html
代码：未开源
摘要
细粒度的3D分割是3D对象理解中的一项重要任务，尤其是在智能制造或3D对象的零件分析等应用中。然而，此类问题中涉及的许多挑战仍有待解决，例如i)解释3D对象不同区域的复杂结构；ii)捕获具有足够拓扑正确性的细粒度结构。当前的深度学习和图机器学习方法无法应对这些挑战，因此在细粒度3D分析中表现不佳。在这项工作中，拓扑数据分析方法与几何深度学习模型相结合，用于3D对象的细粒度分割任务。我们提出了一种新的神经网络模型，称为基于持久同源的图卷积网络（PHGCN），i）将持久同源集成到图卷积网络中，以捕获能够准确表示3D对象复杂结构的多尺度结构信息；ii)应用一种新颖的持久性图损失(LPD)，为细粒度结构上的分割提供足够的拓扑正确性。细粒度3D分割的大量实验验证了所提出的PHGCN模型的有效性，并显示出对当前最先进方法的显着改进。
1、引言
细粒度3D语义分割是一项对每个3D点输入的标签进行语义分类的任务。对于智能制造、自动室内设计和家具布置、自主机器人操作、人机交互、3D服装分析等许多对3D形状进行详细处理和分析的应用来说，这是一项必不可少的任务。
由于细粒度3D对象的特定属性，分割细粒度3D对象涉及许多挑战，例如i)位于不同区域的复杂结构如何分割；ii)形状相关的拓扑结构（例如，物体的把手、门把手、设备线）如何分割。这些属性总是表现在细微的部分或多个小的连接组件中，这对于下游任务（例如机器人操作）在语义上很重要。充分解释这两个主要结构对于准确的3D细粒度语义分割任务至关重要。未能解决这些挑战将大大降低语义理解3D细粒度对象的性能并产生不连贯的分割输出，这对于智能制造和机器人操作至关重要。
近年来，基于深度神经网络的方法[6,16,21]和几何学习方法[15,27,28]已成为3D点云理解任务中的主流方法，从一般的3D对象分类到语义对象和场景的分割。回顾这些方法，发现它们并不是专门为理解具有复杂结构或形状相关拓扑结构的细粒度3D对象的任务而设计的。[15,27,28]中的方法应用图神经网络(GNN)或图卷积网络(GCN)模型从3D点云中的几何结构中提取特征。然而，这种方法仅捕获由边表示的成对关系，因为在GNN/GCN模型中构建的相邻图仅表示3D点云之间的成对关系。因此，细粒度3D对象的复杂结构中存在的高维关系无法被精细捕获。最近的工作PartNet模型[31]应用级联二进制标记来表示用于分层分割的自上而下的递归部分分解。然而，二进制标记的表示能力受到层次结构深度的限制，因此难以处理具有多个复杂结构的3D对象。
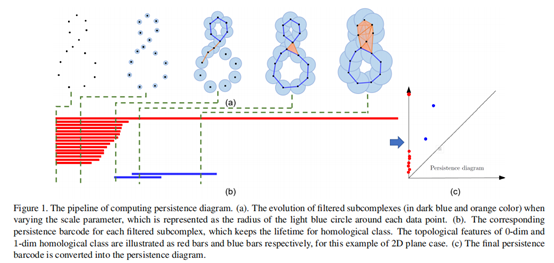
事实上，复杂结构中存在的几何和拓扑信息是理解细粒度物体形状的基本线索。拓扑数据分析(TDA)[3]是一个新兴领域，它从复杂数据中推断出相关的拓扑和几何特征。TDA使用一种称为复形过滤的机制来构建输入点云的多尺度拓扑结构，提取点云复杂结构中存在的高维关系，如图1（a）。然后，将TDA中的一个工具持久同源应用于生成的严格递增子复形的嵌套序列，称为过滤复形，以计算多尺度拓扑特征，表示为持久条形码和持久图，如图1（b）和（c）所示。生成的持久性图中的0-dim、1-dim和2-dim持久同调特征对应于点云中的连接组件、圆圈和更高维对应物（例如空腔）。
在这项工作中，我们选择了TDA工具[10]来提出一种新的网络模型，称为基于持久同源的图卷积网络（PHGCN），它将持久同源特征结合到GCN网络中，以增强其捕获细粒度3D对象的复杂结构中的多尺度拓扑特征的能力。
为了进一步解决细粒度分割问题，我们发现细粒度对象依赖于形状的拓扑结构，尤其是连接部分（例如手柄、电线、旋钮）总是表现为小尺寸对象或薄连接组件，这也使得相关分割变得困难，因为在分割任务中通常使用的交叉熵损失可能无法充分反映拓扑错误，即使整体损失值很低。为了克服这个问题，我们提出了一种持久性图损失（ ），它作为拓扑约束来确保分割输出具有足够的拓扑正确性，从而获得连贯的分割输出。
据我们所知，我们的工作是第一个引入持久同源性来解决细粒度3D语义分割问题的工作。我们工作的主要贡献总结如下：
1.凭借持久的同调特征，一种新颖的GCN网络模型能够捕获细粒度3D对象中复杂结构的多尺度拓扑特征。
2.应用一种新的持久性图损失来加强预测中的拓扑正确性，以提供连贯的细粒度分割输出。
3.所提出的工作证明了用计算拓扑方法扩展通用GNN/GCN结构的可行性。
在具有挑战性的3D对象部件分割基准上评估了细粒度语义分割的广泛实验，这表明所提出的PHGCN模型实现了最先进的结果。
2、拓扑数据分析的预备知识
拓扑数据分析（TDA）[3]是一个新兴领域，其目标是从复杂结构的数据中捕获相关的拓扑和几何特征。在本节中，提供简要概述以突出TDA中的机制。TDA的详细信息可以在开创性论文[11,33]中找到。
2.1 单纯复形
由于没有从数据点中提取拓扑信息的直接方法，因此将单纯复形构造为对采样点的基本形状的拓扑近似。单纯复形可以看作是图的高维扩展，它包含不同维度的单纯形的集合。k-dim单纯形的几何实现分别是顶点（k=0）、边（k=1）、三角形（k=2）、四面体（k=3）和高阶对应物（k⩾4）。
2.2 同调群
为了计算分析单纯复形的拓扑特征，将同调群分配给单纯复形。同调群是描述单纯复形在不同维度上的拓扑特征的一种数学群。k-dim同调群的拓扑特征分别指连通分量（k=0）、圆圈（k=1）和空腔（k=2）。
2.3 持久同源性和过滤
持久性是一种在给定参数变化时形状如何变化的度量。持久同源性提供了一种跟踪拓扑特征在某些参数（例如每个数据点的规模）变化期间何时出现和消失的方法。在此期间，会生成一个嵌套的单纯复形序列，也称为过滤，如图1（a）所示。过滤通过增加尺度参数来捕捉单纯复形的演化过程，尺度参数可视为数据点下的多尺度拓扑空间。因此，每个多尺度拓扑特征的生命周期被记录为持久性条形码，如图1（b）所示。然后可以将持久性条形码转换为每个拓扑特征的出生时间和死亡时间，并表示为持久性图，如图1（c）所示。最终，捕获了数据点中的形状的多尺度拓扑信息。
3、相关工作
在本节中，将讨论两种主要的相关技术：点云上的深度学习方法和持久同源方法。
3.1 点云深度学习
基于深度神经网络的方法在2D图像语义分割任务中的成功[7,23,32]，提高了其在3D点云输入方面的可行性[6,16,17,21,30]。然而，这些方法在捕获点之间的连接方面缺乏足够的能力。基于图的方法，如DGCNN[28]、ResGCN-28[15]，通过将每个点设置为节点并通过测量点对之间的相关性来构建边，明确地从点云构建图。然而，此类方法仅捕获点之间的成对关系，并且难以捕获复杂结构的高阶关系，高阶关系在细粒度对象中很普遍。
3.2 机器学习中的持久同源性
持久同源性是拓扑数据分析中的一种基本方法，用于从不同空间分辨率的几何实现中提取拓扑特征。提取的拓扑特征提供了对数据底层形状的洞察，并作为部署在机器学习管道中的强大特征发挥作用[1,2,14]。因此，TDA方法的有效性吸引了计算拓扑方法在各种应用中的广泛采用，包括动作识别[25]、医学成像[8,22]、形状匹配[20]和神经网络设计[4,9]。最近的一些工作[12,13]也探索了持久同源性的可微性的可行性。受这些有前途的工作的启发，提出了一种新的PHGCN将持久同源机制与图卷积网络相结合，以捕获细粒度对象复杂结构中的多尺度结构信息。
4、方法
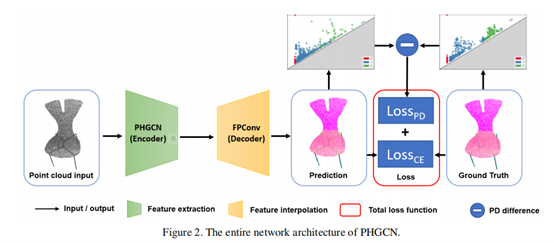
在本节中，我们将详细介绍我们提出的细粒度3D语义分割方法。所提出的方法由两个核心模块组成：1）基于持久同源的图卷积神经网络（PHGCN），通过拓扑持久性（PH）和图卷积网络（GCN）的结合来捕获复杂结构中的多尺度结构信息，2)持久性图损失( )应用于优化中，以减少拓扑误差来实现分割细粒度结构。整个网络架构如图2所示。每个提出的模块的详细信息将在以下部分中描述。
4.1 通用图卷积网络（GCN）
4.2 基于持久同源的图卷积网络(PHGCN)
通过应用顺序GCN层的计算，得到的局部特征图仅捕获局部邻域的特征，这不足以理解3D细粒度对象。在这项工作中，我们采用拓扑数据分析工具来提取隐藏在3D细粒度对象的复杂结构中的基本信息。
持久同源性(PH)是一种来自拓扑数据分析的数学工具，能够提取点云形状中的可证明稳定的拓扑特征。为了克服通用GCN模型无法捕获3D细粒度对象的复杂结构的问题，我们通过集成PH模块来扩展GCN模型，以提取复杂结构中的基本拓扑信息。
PH模块中描述了提取持久同源特征的方法，如图3（b）所示：N个3D点的输入点云可以被认为是一个有限度量空间，记为X_N，过滤结构被应用在X_N中，以通过不同的尺度参数，提取一系列多尺度被过滤的单纯复形，记为Filt(X_N)。然后，应用持久同源性计算拓扑特征的演化和拓扑特征出现时间和消失时间之间的时间段，记为出生时间b和死亡时间d。这样的周期通常由持续图（PD）来描述，它是二维平面中的点集，其中每个点（b，d）代表第k个持续同源类，它在时间b出现并在时间d消失（维度k=0,1,2分别指连接组件、圆圈和空腔）。生成的PD反映了对解释复杂结构至关重要的多尺度拓扑信息。
4.3 持久性图损失Lpd
因此，拓扑约束被附加在优化中，以增强分割输出中的连贯性和连通性，特别是对于具有形状相关拓扑结构的细粒度对象。
4.4 网络架构
参考Pointnet++[21]的网络架构设计，我们提出的PHGCN模型采用编码器解码器样式[21,27,29]进行部件语义分割任务。编码器模块包含四个图卷积网络（GCN）层，它们被认为是局部特征的提取器。然后，提取的局部特征与从复杂结构中由持久同源（PH）模块捕获的拓扑特征融合。为了对编码器下采样的特征进行上采样，由四个FPConv层组成的解码器模块用于逐渐将特征内插为输入的原始大小。为了进行优化，使用3D对象的每个部件类别的预测值和真实值来计算PD损失Lpd，然后将其与交叉熵损失Lce集成。
5、实验
5.1 ShapeNet-Part数据集的分割
ShapeNet-Part[5]数据集是3D细粒度逐点分割的第一个完整基准。它包含来自16个类别的16,881个CAD形状实例，并在2,048个采样点上标注了零件标签。零件标签共有50种。每个类别都标注有两到五个零件标签。
对于定量评估，我们按照PointNet[6]的设置选择14,007个形状实例作为训练集，其余2,874个作为验证集进行准确性评估。每个实例的2,048个采样点的3D坐标用作输入。
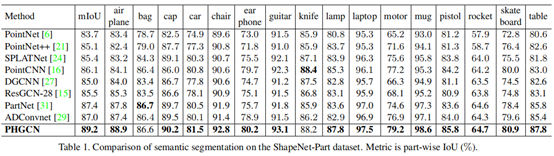
定量和定性结果：ShapeNet-Part数据集评估的定量结果在表1中提供。part-wise Intersection-over-Union(IoU)用作我们评估中的指标，并针对每个对象类别给出和平均值（mIoU）。结果表明，所提出的PHGCN提供了最佳结果，部件mIoU为89.2%，优于所有其他竞争方法。具体来说，PHGCN在结构复杂的细粒度物体（如台灯、吉他）和具有较薄部件的物体（如耳机、杯子、桌子和椅子）上取得了显着的增益，这说明PHGCN中的持久同源机制在解释细粒度对象的复杂结构和形状相关拓扑结构方面发挥了作用。
ShapeNet-Part数据集验证集的定性分割结果如图4(a)所示，其中PHGCN模型的预测与地面真实部分标签注释非常一致，即使ShapeNet-Part数据集包含一个复杂结构和薄零件中的许多形状。为了更好地了解提取的拓扑特征的有效性，我们对两种具有代表性的几何深度学习方法（DGCNN、ResGCN28）进行了定性比较。在图4(b)中，对于具有细粒度部分的对象（灯和杯子），分割（DGCNN、ResGCN-28）在小组件上存在连接断开和错误分类的问题，而PHGCN提供了连贯的分割足够的拓扑正确性。对于具有多尺度和复杂结构的对象（电机），分割（DGCNN，Res28GCN）显示车轮附近的手柄和部件被错误分割，而PHGCN的输出足够准确作为地面实况。
5.2 PartNet数据集上的分割
所提出的PHGCN模型在称为PartNet[18]数据集的更大、更复杂的基准上进一步评估。PartNet[18]数据集包含26,671个形状实例，并分为573,585个具有细粒度零件注释的零件实例。它涵盖了24个对象类别。
在这些品类中，还有一些结构复杂的品类，如台灯、水龙头、椅子等。此外，某些类别（例如门、冰箱、耳机）包含薄且语义上重要的部分，例如耳机线、门把手或冰箱。PartNet数据集的所有这些属性都给准确分割带来了巨大挑战。
对于定量评估，我们按照PartNet[18]的设置将数据集分成训练集、验证集和测试集，比例分别为70%、10%、20%。每个输入实例是从每个CAD模型中采样的10,000个点，并且仅使用3D坐标作为输入。为了验证我们提出的方法在细粒度对象分割上的有效性，选择PartNet（17个类别）的精细级别（level-3）进行评估。
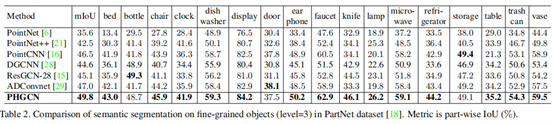
定量和定性结果：在表2中，PHGCN的结果与PartNet数据集上的几种最先进的方法进行了比较。比较结果表明，所提出的PHGCN模型执行所有先前的最先进的方法，如PointNet++[21]、PointCNN[16]、ResGCN[15]、ADConvnet[29]，据报道通过每个类别的部分IoU和所有类别的平均IoU。特别是，PHGCN相对于图深度学习方法（例如DGCNN和ResGCN-28方法）提供了超过10%的相对改进。据观察，具有复杂结构的细粒度物体（如水龙头、灯和椅子）可以以更高的精度进行分割。连同这一结果，与其他最先进的方法相比，所提出的PHGCN与具有薄部件的物体（如耳机、门和冰箱）相比，实现了显着的精度提升。这是分割细粒度3D对象（即薄部分）的意义和最重要的一点，而现有的最先进方法可能无法在薄部分上获得更高的精度。通过应用持久同源方法，所提出的PHGCN更有效地捕获了这些薄部分的结构信息，从而给出了PHGCN提供更高准确性的原因。
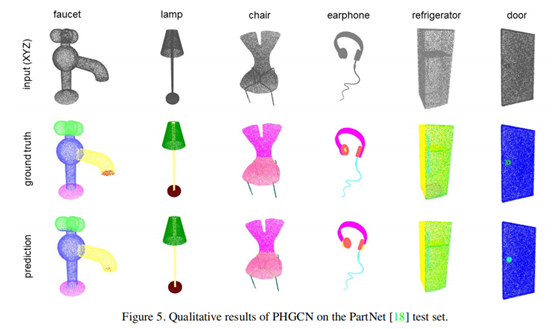
5.3 消融分析
消融分析在ShapeNetPart和PartNet数据集上进行，以验证所提出的PHGCN模型的有效性。消融结果如表3所示。
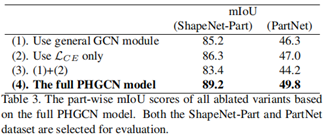
(1)。用通用GCN模块替换PHGCN模块。PHGCN的持久同源机制使模型能够以多尺度的方式从复杂结构中提取拓扑信息。作为比较，一般的GCN层仅捕获局部邻域中成对结构的信息。结果，性能大大降低。
(2)。仅使用Lce。 Lpd损失函数为细粒度结构上的相干分割提供了足够的拓扑正确性。通过从方程式（5）中删除Lpd，由于不连贯的分割输出，性能降低。
表3比较了所有消融变体的部分mIoU分数。得出的结论是：i)最重要的成分来自PHGCN模块，因为多尺度结构信息在细粒度对象中是必不可少的。ii) 的作用显示了性能中的下一个重要因素，特别是对于具有薄部件的细粒度对象。从这项消融研究中可以看出，所提出的模块和损失函数（构成完整的PHGCN模型）达到了最先进的精度。
5.4 持久性图的复杂性分析
为了在保持所提出模型的性能的同时降低计算成本，我们应用了Alpha复杂过滤而不是耗时的过滤，例如VietorisRips或Cech复杂过滤。ShapeNet-Part实例计算PD的平均运行时间为0.25秒（使用Inteli7CPU），这在我们的场景中已经足够合适了。
6、结论
在这项工作中，提出了一种新的基于点云的神经网络模型，称为PHGCN，它集成了计算拓扑方法来解决细粒度3D对象语义分割中的几个挑战。所提出的PHGCN将持久同源机制应用于图卷积网络以处理具有多尺度复杂结构的输入。它还应用 损失函数来加强预测中的拓扑正确性，以提供连贯的细粒度分割输出。
通过这两项改进，细粒度对象（尤其是结构复杂的对象，如水龙头、台灯、椅子和具有薄部件的对象，如耳机、门和冰箱）的分割结果在准确度上得到了显着提高。PHGCN的性能在两个具有挑战性的基准上的准确性方面得到了验证。从实验来看，PHGCN优于几种最先进的基于点云的分割方法。实验结果也验证了PHGCN的贡献：i）基于持久同源性的GCN是一种从3D对象中捕获多尺度结构信息的有效机制；ii)对于细粒度结构，具有足够拓扑正确性的更准确和连贯的语义分割；iii)比最先进的几何深度学习方法具有更高的准确度（例如，在PartNet数据集评估上比DGCNN和ResGCN-28方法相对提高10%以上）。
