论文笔记:(ICML2020)On Learning Sets of Symmetric Elements
论文地址:https://arxiv.org/abs/2002.08599
摘要
从无序集合中学习是一种基本的学习方法,近年来受到越来越多的关注。
这方面的研究主要集中在用特征向量表示集合元素的情况下,而很少关注集合元素本身遵循其自身对称性的常见情况。这种情况涉及到许多应用,从图像的去模糊到多视图三维形状识别和重建。
在本文中,我们提出了一个学习一般对称元素集合的原则方法。我们首先描述线性层的空间,这些层对于元素的重新排序和元素的内在对称性都是等变的,就像图像中的平移。我们进一步证明由这些层组成的网络,称为对称元素层的深度集合(DSS),是不变函数和等变函数的通用逼近器,而且这些网络比孪生网络具有更严格的表达性。DSS层的实现也很简单。
最后,我们用图像、图和点云进行了一系列实验,证明了它们比现有的集和学习架构有所改进。
一、引言
从3D数据(Zaheer等,2017;Qi等,2017;Su等,2015年;Kalogerakis等人,2017年)的分类和分割到图像去模糊(Aittala & Durand, 2018年)来看,利用由无序元素集合组成的数据进行学习是一个应用广泛的重要问题的。在此情况中,每个数据点由一组元素组成,任务与元素顺序无关。这种独立性引出了一种对称结构,可用于深度模型的设计,提高了效率和泛化性。的确,遵循集合对称性的模型,例如(Zaheer等,2017;Qi等,2017),已成为解决此类任务的主导方式。然而,在许多情况下,集合本身的元素遵循某些对称性,就像在学习图像集合、点云集合和图集合时发生的那样。利用这些额外的对称性的最佳方式是什么仍然是未知的。
处理每个元素对称性的一种常见方法是基于单独处理元素。首先,使用孪生架构将每个集合元素独立处理为特征向量(Bromley et al., 1994),然后在所有特征向量之间融合信息。当遵循这个过程时,集合元素之间的交互只在每个元素已经被处理之后才发生,可能会忽略底层的细节。事实上,最近的研究表明,对于学习一组图像来说(Aittala & Durand, 2018;Sridhar等人,2019年;刘et al ,2019),中间信息共享层可以实现显著收益。
在本文中,我们提出了一个学习对称元素集合的原则方法。首先,我们描述了这些集合的对称群,然后充分刻画了线性层的空间,这些线性层与这个群是等变的。值得注意的是,这个特性意味着集合元素之间的信息应该在所有层中共享。例如,图1演示了一组图像的DSS层。DSS层提供了一个统一的框架,该框架为各种数据类型概括了前面描述的几个体系结构。特别是,它直接概括了深度合集(Zaheer等,2017)。此外,最近的其他作品也可以视为我们方法的特殊案例(Hartford et al., 2018;Aittala&杜兰,2018;Sridhar等人,2019)。

等变架构的一个潜在问题是,整形层对某些对称的等变可能会降低模型的表达能力(Maronet al., 2019c; Morris et al., 2018; Xu et al., 2019)。通过证明两个不变和等变DSS网络的通用逼近定理,消除了这一潜在的限制。简单地说,这些定理说明如果不变(等变)网络对于感兴趣的元素是通用的,那么相应的不变(等变)DSS网络在这些元素的集合上也是通用的。这些结果的一个重要推论是DSS网络严格地比孪生网络更有表现力。
综上所述,本文有三个主要贡献:
(1)我们刻画了具有对称元素集合的线性等变层空间。
(2)证明了由DSS层组成的网络的两个通用逼近定理。
(3)我们展示了DSS层在一系列任务中的经验效益,从分类、匹配到选择,应用于从图像到图形和3D点云的各种数据。这些实验表明,与以前的方法相比,这些方法有了一致的改进。
二、先前的工作
集合学习 几项研究设计的网络架构将结构化的集合作为输入。Vinyals等人(2015) 建议扩展Sutskever等人(2014)的序列对序列的框架来处理集合。Ravanbakhsh et al. (2016); Edwards & Storkey(2016); Zaheer et al. (2017); Qi et al. (2017)突出工作提出使用标准前馈神经网络,其层被约束为对排列的等变。当与集合池化层结合时,这些模型也被证明是连续置换不变函数的通用逼近器。Wagstaff等人(2019)提供了一个理论上的 关于函数表示局限性的研究 在具有这种网络的集合上。Wagstaff等人(2019)从理论上研究了用这种网络在集合上表示函数的局限性。在另一项相关工作中,Murphy等人(2018)建议将置换不变函数建模为置换敏感函数的平均值。
一些研究对学习图像集的具体案例进行了探讨。Su等人(2015);Kalogerakis等人(2017)通过对多个视点渲染的图像进行处理,实现了对三维模型的分类和分割。这些方法使用一个Siamese卷积神经网络来处理图像,然后是视图池化层。Esteves等人(2019)最近考虑了相同的设置,并建议在旋转组的子组上执行卷积,从而实现对所有视图的联合处理。Sridhar等人(2019)处理了从多个视点进行三维形状重建的问题,并建议使用几个等变均值去除层,即从集合中的每幅图像中减去所有图像的均值。Aittala & Durand(2018)针对的是图像去模糊和去噪,建议在卷积块之后使用集合池化层,对于每个像素,将所有图像上的最大值连接到所有图像上。Liu等人(2019)提出将基于注意的信息共享块用于人脸识别任务。在Gordon等人(2020)中,作者通过添加平移等变性假设来修改神经过程,将输入视为一组平移等变对象。
深度学习中的等变性 学习中等变性的典型例子可能是视觉对象识别,其中流行的卷积神经网络(CNNs)是由图像平移等变的卷积层构建的。在过去的几年里,研究人员已经使用不变性和等变性考虑为其他类型的数据设计深度学习架构。除了以上讨论的集合结构数据之外,研究人员还提出了集合(Hartford et al., 2018)、图(Kondor et al., 2018;Maron等人,2019b;陈等,2019年;Albooyeh等人,2019)和关系数据库(Graham & Ravanbakhsh, 2019)。另一项成功的工作考虑了其他的图像对称性,如反射和旋转(Dieleman等人,2016;Cohen & Welling, 2016a;b;Worrall等人,2017年;Cheng等人,2018),球面对称性(Cohen等人,2018;2019 b;Esteves等人,2017年),或3D对称(Weiler等人,2018年;温克尔斯和科恩,2018年;Worrall & Brostow, 2018年;Kondor, 2018;托马斯等人,2018年;维勒等,2018年)。多篇论文从理论角度研究了等变层的性质(Ravanbakhsh et al., 2017;Kondor & Trivedi出版社,2018年;Cohen等人,2019a),并描述了使用这种层的模型的表达能力(Yarotsky, 2018;Maron等人,2019c;Keriven和Peyr ' e, 2019年;前原和NT, 2019年;Segol & Lipman, 2019)。
三、基础
3.1 符号和基本定义

3.2 G-不变网络

3.3 描述等变层

3.4 Deep sets

四、DSS层
我们的主要目标是为元素集合设计深层模型。在这一节中,我们首先表示这些集合的对称群G。我们所提倡的深层模型是由线性g等变层(DSS层)组成的,因此,我们的下一步是寻找这些层空间的简单实用的表征。
4.1 对称元素集合

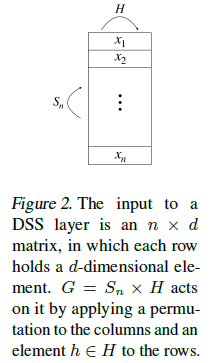
4.2 等变层的表征



五、通用逼近定理

5.1 不变函数


5.2 等变函数


5.3 例子

六、实验


6.1 多种测量分类
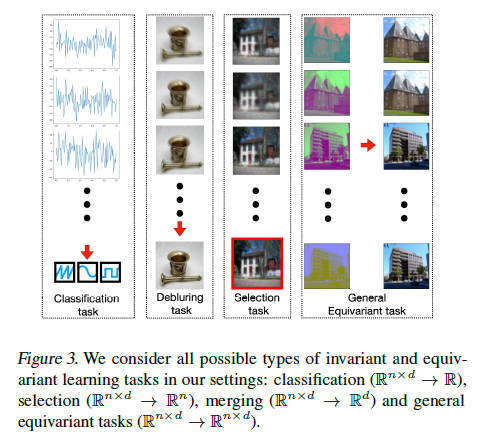
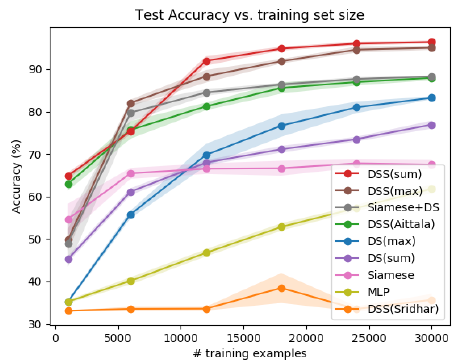
为了说明DSS的好处,我们首先使用我们生成的合成数据集在信号分类任务中对其进行评估。每个样本由在100个时间步长采样的同一个一维周期信号的一组n = 25个噪声测量值组成(参见图3)。清洁信号从三种信号类型-正弦、锯齿波和方波-具有变化的振幅、直流分量、相移和频率均匀采样。任务是在给定一组噪声测量值的情况下预测信号类型。图4描述了分类准确率随训练集大小的变化,表明DSS(sum)优于其他所有方法。值得注意的是,DSS(和)层达到了显著的更高的精度比深度集合架构,其中考虑到集合的结构,但考虑元素内对称。DSS(sum)的性能也优于Siamese和Siamese+DS体系结构,它们不采用早期聚合。DSS(Sridhar)失败了,大概是因为它采用了一种平均去除聚合方案,而这种方案不适合这个任务(去除信号,留下噪声)。
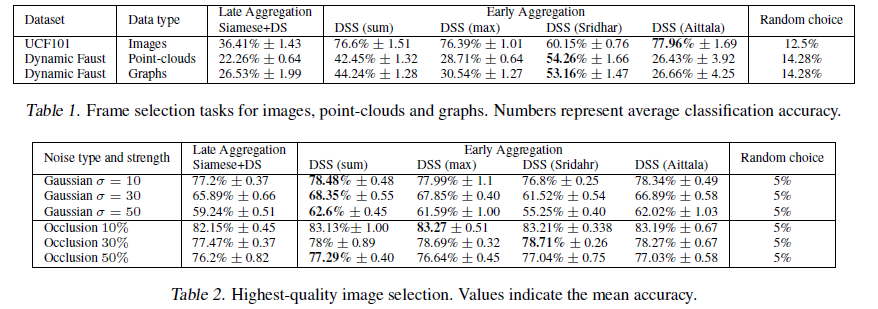
6.2 选择任务


6.3 颜色通道匹配


6.4 图像去模糊

6.5 实验总结

七、总结
在本文中,我们提出了一种原则性的方法来设计具有对称性的元素集合的深度网络:我们已经描述了这类集合的等变映射空间,分析了它的表达能力,举例说明了它在各种任务和数据类型上优于标准集合学习方法的优点,并证明了我们的方法概括了之前的一些成功的工作。


