邮件加密和签名
转自
http://www.cnblogs.com/bitzhuwei/archive/2012/10/26/An_Introduction_to_Cryptography_and_Digital_Signatures.html
本文据图解释一下如何通过公钥私钥实现邮件的加密、解密以及数字签名,从而保证邮件的安全发送和接收。
上图先:
做事之前最好先搞搞清楚我们要做什么。本文要讲的是如何保证邮件(或者消息、check,随便怎么称呼吧)在网络传输中的安全。具体的说,就是要保 证邮件只能由指定的那个接收者(recipient)读到,并且只能由指定的发送者(sender)发送。这样就算是实现了从发送至(sender)到接 收者(recipient)的信息安全。
那我们先从问题1“保证邮件只能由指定的那个接收者读到”这个问题开始。
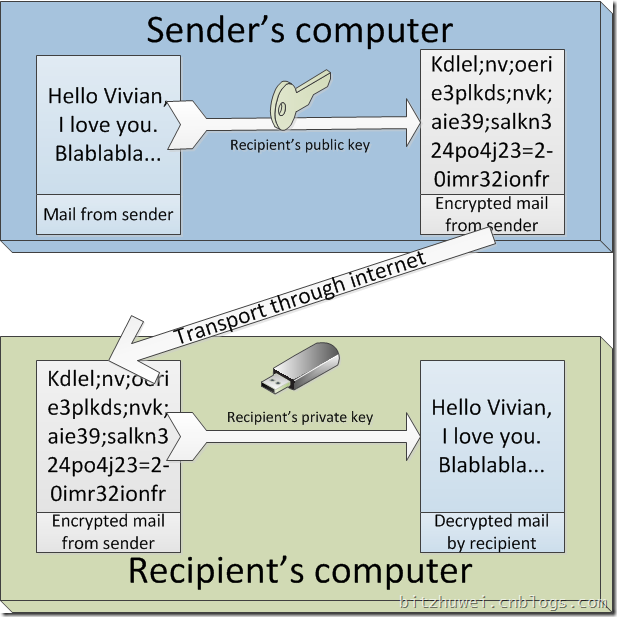
从宏观上说,只能由指定的recipient读到,就是说这个recipient有别人都没有的东西才行。这个recipient独有的东西,就是 他的私钥(private key)。私钥就是一个字符串,只有recipient知道这个字符串是什么,与其对应的还有公钥(public key),公钥是所有人(发送者和想非法获取邮件内容的人)都可以知道的。recipient自己制作出私钥自己保留,自己制作出公钥发布到网上。公钥可 以对邮件进行加密,但不能解密;私钥可以对邮件进行解密,但不能加密(这叫非对称加密asymmetric encryption)。于是发送者(sender)用公钥将邮件加密,然后发送给接收者(recipient)。接收者收到加密的邮件,直接看的话就是 一堆乱码,然后他用私钥解密,就读到了邮件原文内容。
现在,有个坏人想读邮件内容,就算他黑到了从网上传送的邮件,也是加密了的,没有私钥他无法解密,也就读不到邮件原文了。(这里我们要相信加密解密的算法,这是基础。否则什么安全都无法实现了)
到此,图示应该是这样的:
我要是那个坏蛋,我就想,如果我读不到原文,我也不让那个真正的接收者(recipient)读到,我把加密的邮件改了(公钥人人都可以拿到),或者重新写一个邮件,加密一下,冒充发件人(sender)发给你,让你也受点罪。
所以我们就需要保证能够确认发送者(sender),或者说,只能由那个发送者发送这个邮件,如果有其他人中途修改了邮件,我们可以识别出来。这就是问题2。
再次从宏观上看,这里是要求发送者(sender)有某种别人都没有的东西。这个就是发送者的私钥(private key)!没错思路是和上面一样的!
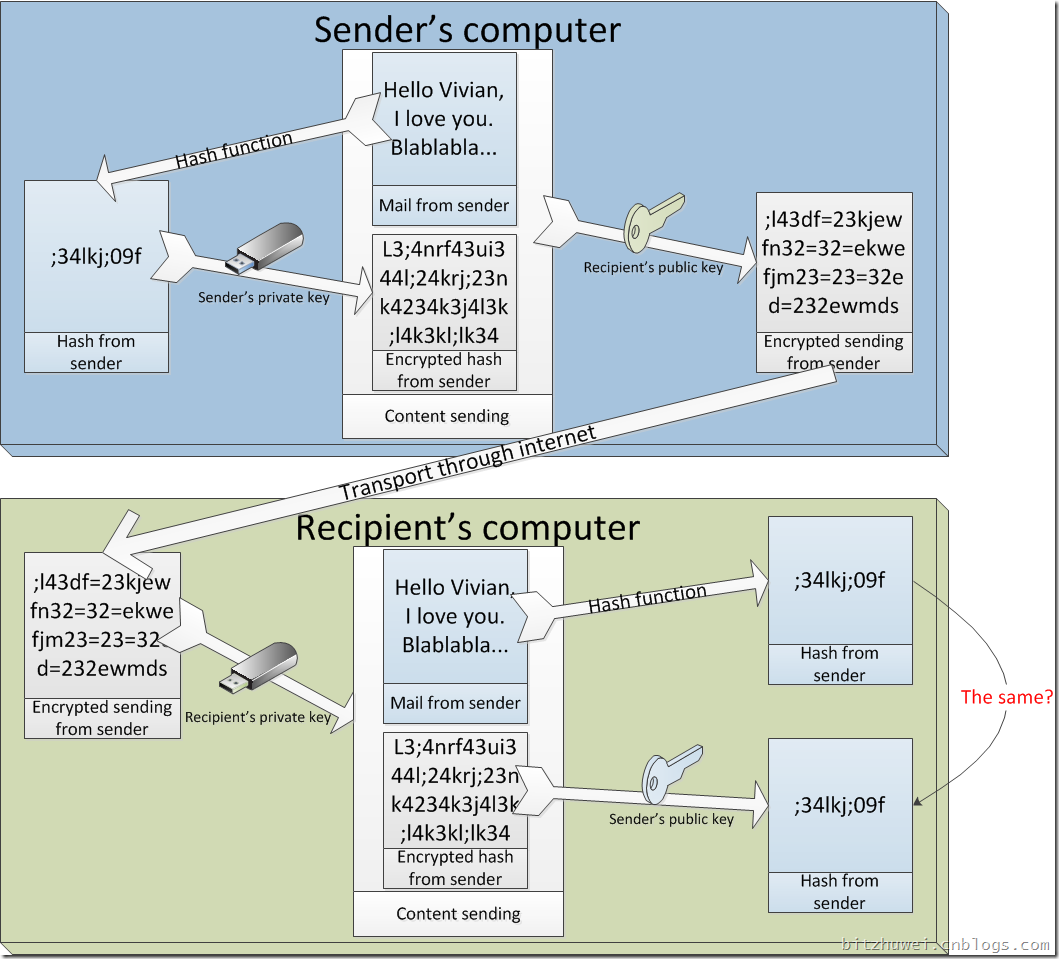
发送者(sender)对即将发送的邮件计算一个hash值(可以认为是一个字符串,这是常用的方法),然后用自己的私钥(private key)对hash值加密,然后将邮件和加密了的hash值一起用接收者的公钥(public key)加密,通过internet发送给接收者(recipient)。接收者(recipient)收到加密的邮件,用自己的私钥(private key)解密,得到邮件原文和加密的hash值,用发送者的公钥对hash解密,得到原始的hash值,最后自己对邮件原文进行hash计算,如果得到的 结果和之前收到的hash值解密后的内容相同,就说明这是未被坏人改动过的邮件。
这个过程中,发送者的私钥(private key)用于加密,公钥(public key)用于解密,和之前接收者的公钥、私钥用法是正好相反的,但是两种使用都是非对称的加密解密。
到此,图示应该是这样的:
如果某坏蛋修改了Content sending中的内容,那么接收者(recipient)解密出来的hash值与自己计算出来的hash值是绝对不一样的。(两者一样的概率比中500万小的多了)
至此我们的加密解密工作就算完成了。但是,在实际应用中还有一个变化:非对称加密(asymmetric encryption)是一种比较慢的计算方法,如果邮件内容很多,就不太实用了。于是为了加快速度,就结合了对称加密(symmetric encryption)方法。对称密钥就是说,这个密钥既可以用来加密,也可以用来解密。这个和防盗门的钥匙是一样的,既可以锁门,也可以开门。我称之为 家用防盗门式的加密解密方法。
现在我们引入一个对称密匙,实现对要在不安全的internet上传输的邮件的加密解密。对称密钥必须让发送者和接收者都有才行,同时,为了保证安 全,必须只让接收者和发送者知道对称密钥。那么就得每次发邮件都使用一个一次性的密钥,并且对这个密钥也进行加密(不要晕哦)。所以之前用于对邮件内容加 密的接收者(recipient)的公钥,就改为对这个对称密钥进行加密。因为密钥都是很短的一个字符串,所以计算的慢点也不碍事了,因为要计算的东西少 了嘛。
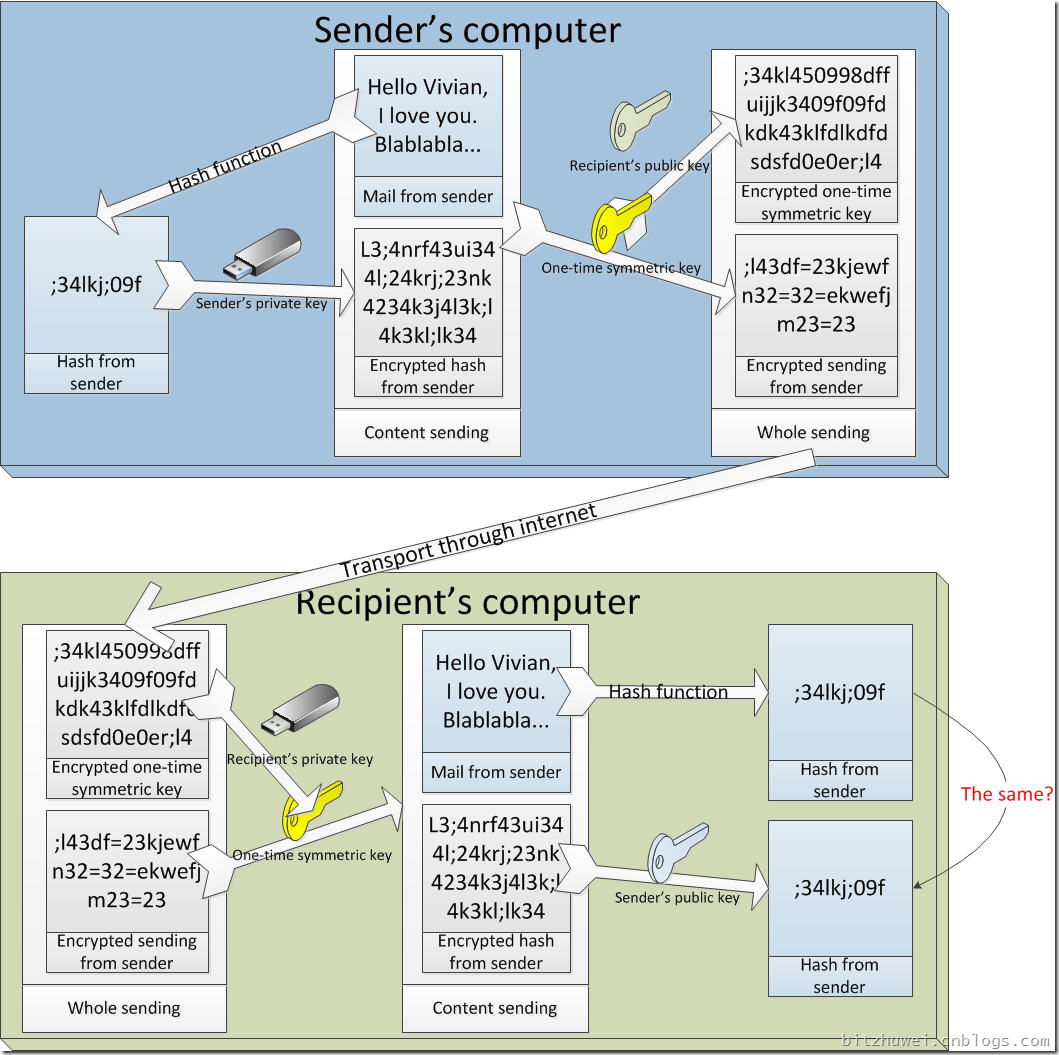
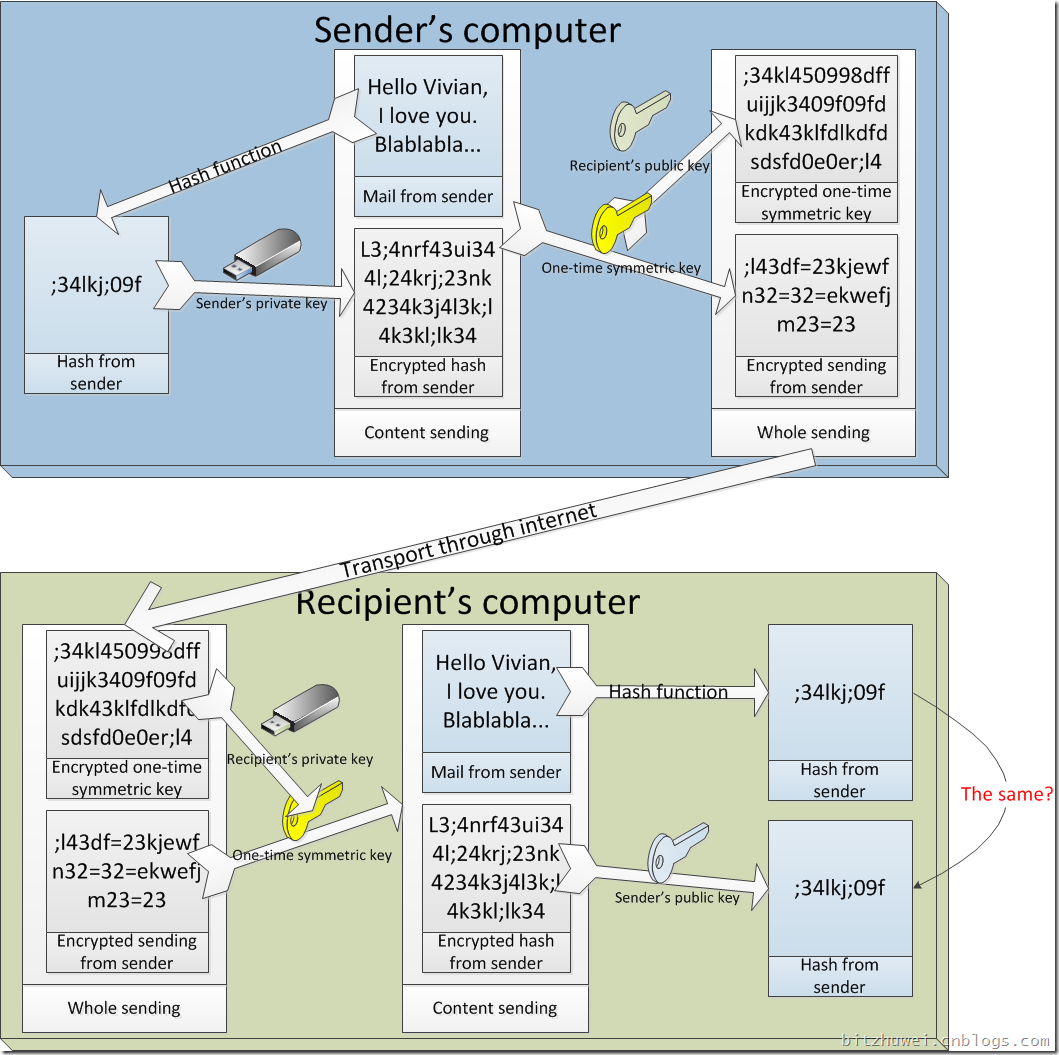
现在就成了下图所示的情况。
这就是本文最初给出的图示的推演过程啦。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号