数据结构--树（遍历，红黑，B树）

平时接触树还比较少，写一篇博文来积累一下树的相关知识。

很早之前在数据结构里面学的树的遍历。

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

例如：求下面树的三种遍历

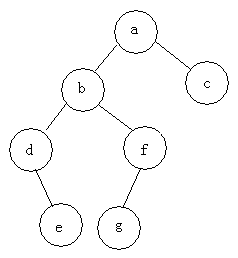
前序遍历：abdefgc

中序遍历：debgfac

后序遍历：edgfbca

下面来记录一下今天在九度上面做的一道上海交大的机试题：

题目描述：

We are all familiar with pre-order, in-order and post-order traversals of binary trees. A common problem in data structure classes is to find the pre-order traversal of a binary tree when given the in-order and post-order traversals. Alternatively, you can find the post-order traversal when given the in-order and pre-order. However, in general you cannot determine the in-order traversal of a tree when given its pre-order and post-order traversals. Consider the four binary trees below:

All of these trees have the same pre-order and post-order traversals. This phenomenon is not restricted to binary trees, but holds for general m-ary trees as well.

（大致意思就是嗯，中序遍历+后序遍历->前序遍历

中序遍历+前序遍历->后序遍历

前序遍历+后序遍历-/->中序遍历（无法确定一棵树））

输入：

Input will consist of multiple problem instances. Each instance will consist of a line of the form
m s1 s2
indicating that the trees are m-ary trees, s1 is the pre-order traversal and s2 is the post-order traversal.All traversal strings will consist of lowercase alphabetic characters. For all input instances, 1 <= m <= 20 and the length of s1 and s2 will be between 1 and 26 inclusive. If the length of s1 is k (which is the same as the length of s2, of course), the first k letters of the alphabet will be used in the strings. An input line of 0 will terminate the input.

有多行输入，每一行输入的格式是s1,s2,s1是前序遍历，s2是后序遍历。遍历序列是一系列的小写字母（序列长度1~26个）。输入0结束。假设树为m叉（1~20）

输出：

For each problem instance, you should output one line containing the number of possible trees which would result in the pre-order and post-order traversals for the instance. All output values will be within the range of a 32-bit signed integer. For each problem instance, you are guaranteed that there is at least one tree with the given pre-order and post-order traversals.

（对每一个输入，你都要输出满足该前序遍历和后序遍历的树的个数，输出的值可以用32位有符号整型来表示。对于每一个输入，至少有一颗满足要求的树）

样例输入：

2 abc cba
2 abc bca
10 abc bca
13 abejkcfghid jkebfghicda

样例输出：

4(就是上面那幅图所示的情况)
1
45
207352860

题解及分析：
m指m叉树，m=2就是二叉树，m=3是三杈树。这个题目想明白了其实就是求对于m叉树而言其每层的叶子节点的组合方式有
多少种。由先序和后序序列其实可以却确定每一层的叶子节点的个数，以及哪些是这一层的叶子节点，唯一不确定的就是
这些节点的位置（但是由先序可以确定这些叶子节点相对位置是确定的），比 如第i层有n个叶子节点
（由先序和后序结合判定出），那么这层就有c(n,m)种组合方式，然后确定某个叶子节点的子树，对其进行递归求解。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int tree[30];//存储子节点数目
long comb(int n,int m)//计算排列组合
{
long result=1;
int i;
for(i=1;i<=n;i++)
result=result*(m-i+1)/i;
return result;
}
void f(char *s1,char *s2,int l)
{
if(l==1)
return;
int i=1,j=0,head=0;
while(i<l)
{
for(;j<l;j++)
if(s1[i]==s2[j])
break;
f(&s1[i],&s2[head],j-head+1);//处理子串
tree[s1[0]-'a']++;//子树数目
i=j+2;//下一颗子树起始处
head=j+1;
}
}
int main()
{
int m,l,i;
long sum;
while(scanf("%d",&m)!=EOF)
{
sum=1;
memset(tree,0,sizeof(tree));
char s1[30],s2[30];
scanf("%s%s",s1,s2);
l=strlen(s1);
f(s1,s2,l);
for(i=0;i<30;i++)
sum*=comb(tree[i],m);//结果为所有排列组合之积
printf("%ld\n",sum);
}
return 0;
}

最后，科普一下红黑树和B树。

在别人面试的博客里面经常看到红黑树来着，但是自己一直不知道是什么；

还有软件安全课的时候，老师讲到ntfs文件系统的索引结构是B+tree,也不理解。

趁这个写博客的机会，让自己学习一下~~~~~

红黑树：红黑树应用很广，大量应用在底层数据结构中，主要用于存储和查找。平日开发很少自己去写红黑树，因为我们大部分都是使用别人封装后的接口而已，但是深入了解数据结构和算法是非常必要的。

之前看了很多写红黑树的博客，但是感觉都讲的不太清楚！没说这样操作如何使他保持平衡的，于是疑惑重重，就看不下去了，一次不经意看到一个人说维基百科的红黑树讲的好，我就随便点了一下一看——这下疯了~，怎么讲的这么好！可以说是把一个复杂的问题，讲得简单化！这太幸福了！于是我就慢慢学会了！强烈推荐维基的这个讲解，再也找不到比这还好的讲解了！不知道它上边其它的怎么样，反正这个很好！！既然学会了，走过来了，我也要留下脚印！

下面将是我对红黑树的总结，里面的性感的图片都是维基百科红黑树上的^_^！我讨论的红黑树需建立在会平衡二叉树的基础上去学，即若不懂“旋转”操作，请看平衡二叉树的旋转操作。

红黑树（RBT）的定义：它或者是一颗空树，或者是具有一下性质的二叉查找树：

1.节点非红即黑。

2.根节点是黑色。

3.所有NULL结点称为叶子节点，且认为颜色为黑。

4.所有红节点的子节点都为黑色。

5.从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。

看完红黑树的定义是不是可晕？怎么这么多要求！！这怎么约束啊？我刚看到这5条约束，直接无语了，1-3、4还好说，第5点是怎么回事啊？怎么约束？整这么复杂的条件好干啥啊？我来简单说说呵：第3条，显然这里的叶子节点不是平常我们所说的叶子节点，如图标有NIL的为叶子节点，为什么不按常规出牌，因为按一般的叶子节点也行，但会使算法更复杂；第4条，即该树上决不允许存在两个连续的红节点；第5条，比如图中红8到1左边的叶子节点的路径包含2个黑节点，到6下的叶子节点的路径也包含2个黑节点。所有性质1-5合起来约束了该树的平衡性能-- 即该树上的最长路径不可能会大于2倍最短路径。为什么？因为第1条该树上的节点非红即黑，由于第4条该树上不允许存在两个连续的红节点，那么对于从一个节点到其叶子节点的一条最长的路径一定是红黑交错的，那么最短路径一定是纯黑色的节点；而又第5条从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点，这么来说最长路径上的黑节点的数目和最短路径上的黑节点的数目相等！而又第2条根结点为黑、第3条叶子节点是黑，那么可知：最长路径<=2*最短路径。一颗二叉树的平衡性能越好，那么它的效率越高！显然红黑树的平衡性能比AVL的略差些，但是经过大量试验证明，实际上红黑树的效率还是很不错了，仍能达到O(logN)，这个我不知道，我现在不可能做过大量试验，只是听人家这样说，O(∩_∩)O哈哈~但你至少知道他的时间复杂度一定小于2O(logN)!

上边的性质看个10遍，看懂看透彻再看操作！

插入操作

由于性质的约束：插入点不能为黑节点，应插入红节点。因为你插入黑节点将破坏性质5，所以每次插入的点都是红结点，但是若他的父节点也为红，那岂不是破坏了性质4？对啊，所以要做一些“旋转”和一些节点的变色！另为叙述方便我们给要插入的节点标为N（红色），父节点为P，祖父节点为G，叔节点为U。下边将一一列出所有插入时遇到的情况：

情形1：该树为空树，直接插入根结点的位置，违反性质1，把节点颜色有红改为黑即可。

情形2：插入节点N的父节点P为黑色，不违反任何性质，无需做任何修改。

情形1很简单，情形2中P为黑色，一切安然无事，但P为红就不一样了，下边是P为红的各种情况，也是真正要学的地方！

情形3：N为红，P为红，（祖节点一定存在，且为黑，下边同理）U也为红，这里不论P是G的左孩子，还是右孩子；不论N是P的左孩子，还是右孩子。

操作：如图把P、U改为黑色，G改为红色，未结束。

解析：N、P都为红，违反性质4；若把P改为黑，符合性质4，显然左边少了一个黑节点，违反性质5；所以我们把G，U都改为相反色，这样一来通过G的路径的黑节点数目没变，即符合4、5，但是G变红了，若G的父节点又是红的不就有违反了4，是这样，所以经过上边操作后未结束，需把G作为起始点，即把G看做一个插入的红节点继续向上检索----属于哪种情况，按那种情况操作~要么中间就结束，要么知道根结点（此时根结点变红，一根结点向上检索，那木有了，那就把他变为黑色吧）。

情形4：N为红，P为红，U为黑，P为G的左孩子，N为P的左孩子（或者P为G的右孩子，N为P的左孩子；反正就是同向的）。

操作：如图P、G变色，P、G变换即左左单旋（或者右右单旋），结束。

解析：要知道经过P、G变换（旋转），变换后P的位置就是当年G的位置，所以红P变为黑，而黑G变为红都是为了不违反性质5，而维持到达叶节点所包含的黑节点的数目不变！还可以理解为：也就是相当于（只是相当于，并不是实事，只是为了更好理解；）把红N头上的红节点移到对面黑U的头上；这样即符合了性质4也不违反性质5，这样就结束了。

情形5：N为红，P为红，U为黑，P为G的左孩子，N为P的右孩子（或者P为G的右孩子，N为P的左孩子；反正两方向相反）。

操作：需要进行两次变换（旋转），图中只显示了一次变换-----首先P、N变换，颜色不变；然后就变成了情形4的情况，按照情况4操作，即结束。

解析：由于P、N都为红，经变换，不违反性质5；然后就变成4的情形，此时G与G现在的左孩子变色，并变换，结束。

删除操作

我们知道删除需先找到“替代点”来替代删除点而被删除，也就是删除的是替代点，而替代点N的至少有一个子节点为NULL，那么，若N为红色，则两个子节点一定都为NULL（必须地），那么直接把N删了，不违反任何性质，ok，结束了；若N为黑色，另一个节点M不为NULL，则另一个节点M一定是红色的，且M的子节点都为NULL（按性质来的，不明白，自己分析一下）那么把N删掉，M占到N的位置，并改为黑色，不违反任何性质，ok，结束了；若N为黑色，另一个节点也为NULL，则把N删掉，该位置置为NULL，显然这个黑节点被删除了，破坏了性质5，那么要以N节点为起始点检索看看属于那种情况，并作相应的操作，另还需说明N为黑点（也许是NULL，也许不是，都一样），P为父节点，S为兄弟节点（这个我真想给兄弟节点叫B（brother）多好啊，不过人家图就是S我也不能改，在重画图，太浪费时间了！S也行呵呵，就当是sister也行，哈哈）分为以下5中情况：

情形1：S为红色（那么父节点P一定是黑，子节点一定是黑），N是P的左孩子（或者N是P的右孩子）。

操作：P、S变色，并交换----相当于AVL中的右右中旋转即以P为中心S向左旋（或者是AVL中的左左中的旋转），未结束。

解析：我们知道P的左边少了一个黑节点，这样操作相当于在N头上又加了一个红节点----不违反任何性质，但是到通过N的路径仍少了一个黑节点，需要再把对N进行一次检索，并作相应的操作才可以平衡（暂且不管往下看）。

情形2：P、S及S的孩子们都为黑。

操作：S改为红色，未结束。
解析：S变为红色后经过S节点的路径的黑节点数目也减少了1，那个从P出发到其叶子节点到所有路径所包含的黑节点数目（记为num）相等了。但是这个num比之前少了1，因为左右子树中的黑节点数目都减少了！一般地，P是他父节点G的一个孩子，那么由G到其叶子节点的黑节点数目就不相等了，所以说没有结束，需把P当做新的起始点开始向上检索。

情形3：P为红（S一定为黑），S的孩子们都为黑。

操作：P该为黑，S改为红，结束。

解析：这种情况最简单了，既然N这边少了一个黑节点，那么S这边就拿出了一个黑节点来共享一下，这样一来，S这边没少一个黑节点，而N这边便多了一个黑节点，这样就恢复了平衡，多么美好的事情哈！

情形4：P任意色，S为黑，N是P的左孩子，S的右孩子SR为红，S的左孩子任意（或者是N是P的右孩子，S的左孩子为红，S的右孩子任意）。

操作：SR（SL）改为黑，P改为黑，S改为P的颜色，P、S变换--这里相对应于AVL中的右右中的旋转（或者是AVL中的左左旋转），结束。
解析：P、S旋转有变色，等于给N这边加了一个黑节点，P位置（是位置而不是P）的颜色不变，S这边少了一个黑节点；SR有红变黑，S这边又增加了一个黑节点；这样一来又恢复了平衡，结束。

情形5：P任意色，S为黑，N是P的左孩子，S的左孩子SL为红，S的右孩子SR为黑（或者N是P的有孩子，S的右孩子为红，S的左孩子为黑）。

操作：SL（或SR）改为黑，S改为红，SL（SR）、S变换；此时就回到了情形4，SL（SR）变成了黑S，S变成了红SR（SL），做情形4的操作即可，这两次变换，其实就是对应AVL的右左的两次旋转（或者是AVL的左右的两次旋转）。
解析：这种情况如果你按情形4的操作的话，由于SR本来就是黑色，你无法弥补由于P、S的变换（旋转）给S这边造成的损失！所以我没先对S、SL进行变换之后就变为情形4的情况了，何乐而不为呢？

B树：

B树

具体讲解之前，有一点，再次强调下：B-树，即为B树。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，其实，这是个非常不好的直译，很容易让人产生误解。如人们可能会以为B-树是一种树，而B树又是一种一种树。而事实上是，B-tree就是指的B树。特此说明。

我们知道，B 树是为了磁盘或其它存储设备而设计的一种多叉（下面你会看到，相对于二叉，B树每个内结点有多个分支，即多叉）平衡查找树。与本blog之前介绍的红黑树很相似，但在降低磁盘I/0操作方面要更好一些。许多数据库系统都一般使用B树或者B树的各种变形结构，如下文即将要介绍的B+树，B*树来存储信息。

B 树与红黑树最大的不同在于，B树的结点可以有许多子女，从几个到几千个。那为什么又说B树与红黑树很相似呢?因为与红黑树一样，一棵含n个结点的B树的高度也为O（lgn），但可能比一棵红黑树的高度小许多，应为它的分支因子比较大。所以，B树可以在O（logn）时间内，实现各种如插入（insert），删除（delete）等动态集合操作。

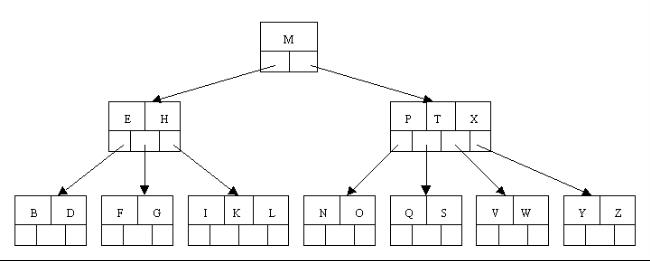
如下图所示，即是一棵B树，一棵关键字为英语中辅音字母的B树，现在要从树种查找字母R（包含n[x]个关键字的内结点x，x有n[x]+1]个子女（也就是说，一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女）。所有的叶结点都处于相同的深度，带阴影的结点为查找字母R时要检查的结点）：

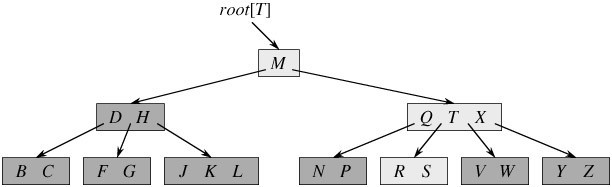
相信，从上图你能轻易的看到，一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女。如含有2个关键字D H的内结点有3个子女，而含有3个关键字Q T X的内结点有4个子女。

B 树又叫平衡多路查找树。一棵m阶的B 树 (m叉树)的特性如下：

树中每个结点最多含有m个孩子（m>=2）；
除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；（读者反馈@冷岳：这里有错，叶子节点只是没有孩子和指向孩子的指针，这些节点也存在，也有元素。@JULY：其实，关键是把什么当做叶子结点，因为如红黑树中，每一个NULL指针即当做叶子结点，只是没画出来而已）。
每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：
       a)   Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。
       b)   Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。
       c)   关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。如下图所示：

针对上面第5点，再阐述下：B树中每一个结点能包含的关键字（如之前上面的D H和Q T X）数有一个上界和下界。这个下界可以用一个称作B树的最小度数（算法导论中文版上译作度数，最小度数即内节点中节点最小孩子数目）t（t>=2）表示。

每个非根的结点必须至少含有t-1个关键字。每个非根的内结点至少有t个子女。如果树是非空的，则根结点至少包含一个关键字；
每个结点可包含之多2t-1个关键字。所以一个内结点至多可有2t个子女。如果一个结点恰好有2t-1个关键字，我们就说这个结点是满的（而稍后介绍的B*树作为B树的一种常用变形，B*树中要求每个内结点至少为2/3满，而不是像这里的B树所要求的至少半满）；
当关键字数t=2（t=2的意思是，tmin=2，t可以>=2）时的B树是最简单的（有很多人会因此误认为B树就是二叉查找树，但二叉查找树就是二叉查找树，B树就是B树，B树的真正最准确的定义为：一棵含有t（t>=2）个关键字的平衡多路查找树）。每个内结点可能因此而含有2个、3个或4个子女，亦即一棵2-3-4树，然而在实际中，通常采用大得多的t值。

B树中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小，根据磁盘驱动(disk drives)的不同，一般块的大小在1k~4k左右)；这样树的深度降低了，这就意味着查找一个元素只要很少结点从外存磁盘中读入内存，很快访问到要查找的数据。

B树的类型和节点定义如下图所示：

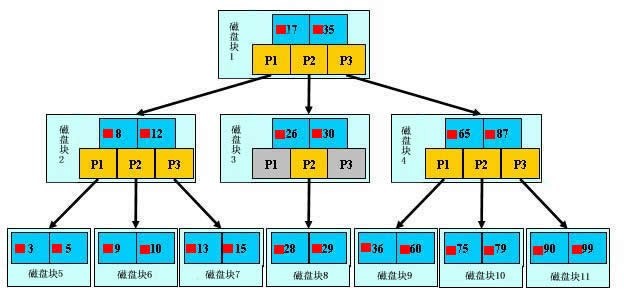
为了简单，这里用少量数据构造一棵3叉树的形式，实际应用中的B树结点中关键字很多的。上面的图中比如根结点，其中17比表示一个磁盘文件的文件名；小红方块表示这个17文件内容在硬盘中的存储位置；p1表示指向17左子树的指针。

其结构可以简单定义为：

typedef struct {

/*文件数*/

int file_num;

/*文件名(key)*/

char * file_name[max_file_num];

/*指向子节点的指针*/

BTNode * BTptr[max_file_num+1];

/*文件在硬盘中的存储位置*/

FILE_HARD_ADDR offset[max_file_num];

}BTNode;

假如每个盘块可以正好存放一个B树的结点（正好存放2个文件名）。那么一个BTNODE结点就代表一个盘块，而子树指针就是存放另外一个盘块的地址。

下面，咱们来模拟下查找文件29的过程：

根据根结点指针找到文件目录的根磁盘块1，将其中的信息导入内存。【磁盘IO操作 1次】
此时内存中有两个文件名17、35和三个存储其他磁盘页面地址的数据。根据算法我们发现17<29<35，因此我们找到指针p2。
根据p2指针，我们定位到磁盘块3，并将其中的信息导入内存。【磁盘IO操作 2次】
此时内存中有两个文件名26，30和三个存储其他磁盘页面地址的数据。根据算法我们发,26<29<30，因此我们找到指针p2。
根据p2指针，我们定位到磁盘块8，并将其中的信息导入内存。【磁盘IO操作 3次】
此时内存中有两个文件名28，29。根据算法我们查找到文,29，并定位了该文件内存的磁盘地址。

分析上面的过程，发现需要3次磁盘IO操作和3次内存查找操作。关于内存中的文件名查找，由于是一个有序表结构，可以利用折半查找提高效率。至于IO操作时影响整个B树查找效率的决定因素。

当然，如果我们使用平衡二叉树的磁盘存储结构来进行查找，磁盘4次，最多5次，而且文件越多，B树比平衡二叉树所用的磁盘IO操作次数将越少，效率也越高。

B树的高度

根据上面的例子我们可以看出，对于辅存做IO读的次数取决于B树的高度。而B树的高度由什么决定的呢？

根据B树的高度公式:

其中T为度数（每个节点包含的元素个数），即所谓的阶数，N为总元素个数或总关键字数。

我们可以看出T对于树的高度有决定性的影响。因此如果每个节点包含更多的元素个数，在元素个数相同的情况下，则更有可能减少B树的高度。这也是为什么 SQL Server中需要尽量以窄键建立聚集索引。因为SQL Server中每个节点的大小为8092字节，如果减少键的大小，则可以容纳更多的元素，从而减少了B树的高度，提升了查询的性能。

上面B树高度的公式也可以进行推导得出，将每一层级的的元素个数加起来，比如度为T的节点，根为1个节点，第二层至少为2个节点，第三层至少为2t个节点，第四层至少为2t*t个节点。将所有最小节点相加，从而得到节点个数N的公式:

两边取对数，则可以得到树的高度公式。

这也就是说每个节点必须至少有两个子元素，因为根据高度公式，如果每个节点只有一个元素，也就是T=1的话，那么高度将会趋于正无穷。

4.B⁺-tree

B⁺-tree：是应文件系统所需而产生的一种B-tree的变形树。

一棵m阶的B+树和m阶的B树的差异在于：

1.有n棵子树的结点中含有n个关键字； (而B 树是n棵子树有n-1个关键字)

2.所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)

3.所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B 树的非终节点也包含需要查找的有效信息)

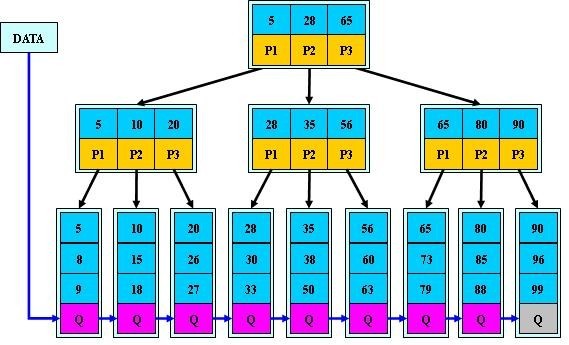
a) 为什么说B⁺-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引？

1) B⁺-tree的磁盘读写代价更低

B⁺-tree的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。

举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B⁺树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B 树就比B⁺树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

2) B⁺-tree的查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

b) B⁺-tree的应用: VSAM(虚拟存储存取法)文件(来源论文 the ubiquitous Btree 作者：D COMER - 1979 )

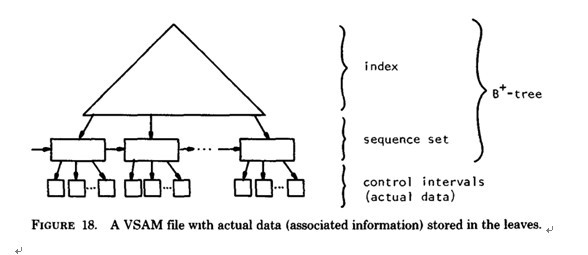
5.B^*-tree

B*-tree是B⁺-tree的变体，在B⁺树非根和非叶子结点再增加指向兄弟的指针；B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。给出了一个简单实例，如下图所示：

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

6、B树的插入、删除操作

上面第3小节简单介绍了利用B树这种结构如何访问外存磁盘中的数据的情况，下面咱们通过另外一个实例来对这棵B树的插入（insert）,删除（delete）基本操作进行详细的介绍。

但在此之前，咱们还得简单回顾下一棵m阶的B 树 (m叉树)的特性，如下：

树中每个结点含有最多含有m个孩子，即m满足：ceil(m/2)<=m<=m。
除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；
每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：
       a)   Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。
       b)   Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。
       c)   除根结点之外的结点的关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1（叶子结点也必须满足此条关于关键字数的性质，根结点除外）。

ok，下面咱们以一棵5阶（即树中任一结点至多含有4个关键字，5棵子树）B树实例进行讲解(如下图所示)：

备注：

关键字数（2-4个）针对--非根结点（包括叶子结点在内），孩子数（3-5个）--针对根结点和叶子结点之外的内结点。当然，根结点是必须至少有2个孩子的，不然就成直线型搜索树了。
曾在一次面试中被问到，一棵含有N个总关键字数的m阶的B树的最大高度是多少?答曰：log_ceil（m/2）N （上面中关于m阶B树的第1点特性已经提到：树中每个结点含有最多含有m个孩子，即m满足：ceil(m/2)<=m<=m。而树中每个结点含孩子数越少，树的高度则越大，故如此）。在2012微软4月份的笔试中也问到了此问题。更多原理请看上文第3小节末：B树的高度。

下图中关键字为大写字母，顺序为字母升序。

结点定义如下：

typedef struct{

int Count; // 当前节点中关键元素数目

ItemType Key[4]; // 存储关键字元素的数组

long Branch[5]; // 伪指针数组，(记录数目)方便判断合并和分裂的情况

} NodeType;

6.1、插入（insert）操作

插入一个元素时，首先在B树中是否存在，如果不存在，即在叶子结点处结束，然后在叶子结点中插入该新的元素，注意：如果叶子结点空间足够，这里需要向右移动该叶子结点中大于新插入关键字的元素，如果空间满了以致没有足够的空间去添加新的元素，则将该结点进行“分裂”，将一半数量的关键字元素分裂到新的其相邻右结点中，中间关键字元素上移到父结点中（当然，如果父结点空间满了，也同样需要“分裂”操作），而且当结点中关键元素向右移动了，相关的指针也需要向右移。如果在根结点插入新元素，空间满了，则进行分裂操作，这样原来的根结点中的中间关键字元素向上移动到新的根结点中，因此导致树的高度增加一层。如下图所示：

1、OK，下面咱们通过一个实例来逐步讲解下。插入以下字符字母到一棵空的B 树中（非根结点关键字数小了（小于2个）就合并，大了（超过4个）就分裂）：C N G A H E K Q M F W L T Z D P R X Y S，首先，结点空间足够，4个字母插入相同的结点中，如下图：

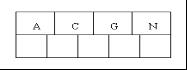
2、当咱们试着插入H时，结点发现空间不够，以致将其分裂成2个结点，移动中间元素G上移到新的根结点中，在实现过程中，咱们把A和C留在当前结点中，而H和N放置新的其右邻居结点中。如下图：

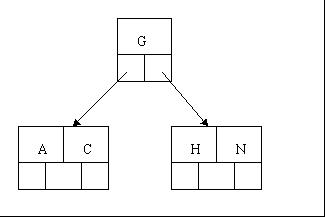
3、当咱们插入E,K,Q时，不需要任何分裂操作

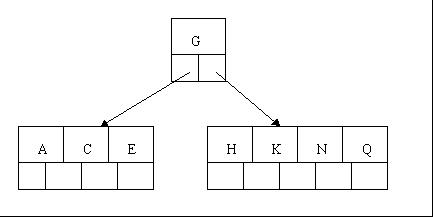
4、插入M需要一次分裂，注意M恰好是中间关键字元素，以致向上移到父节点中

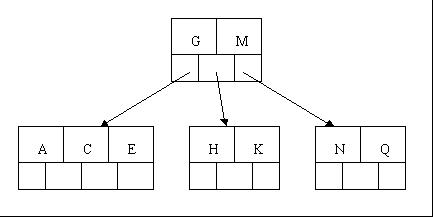
5、插入F,W,L,T不需要任何分裂操作

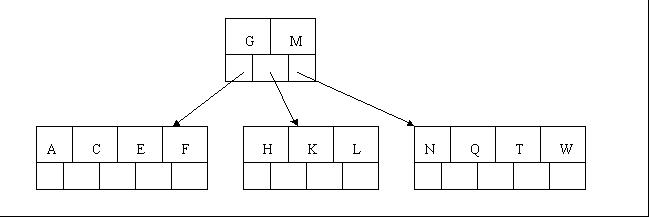
6、插入Z时，最右的叶子结点空间满了，需要进行分裂操作，中间元素T上移到父节点中，注意通过上移中间元素，树最终还是保持平衡，分裂结果的结点存在2个关键字元素。

7、插入D时，导致最左边的叶子结点被分裂，D恰好也是中间元素，上移到父节点中，然后字母P,R,X,Y陆续插入不需要任何分裂操作（别忘了，树中至多5个孩子）。

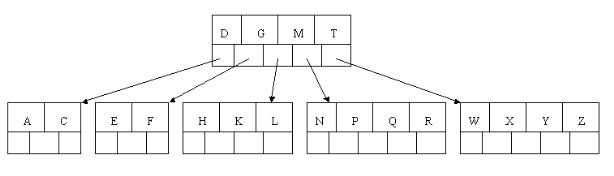
8、最后，当插入S时，含有N,P,Q,R的结点需要分裂，把中间元素Q上移到父节点中，但是情况来了，父节点中空间已经满了，所以也要进行分裂，将父节点中的中间元素M上移到新形成的根结点中，注意以前在父节点中的第三个指针在修改后包括D和G节点中。这样具体插入操作的完成，下面介绍删除操作，删除操作相对于插入操作要考虑的情况多点。

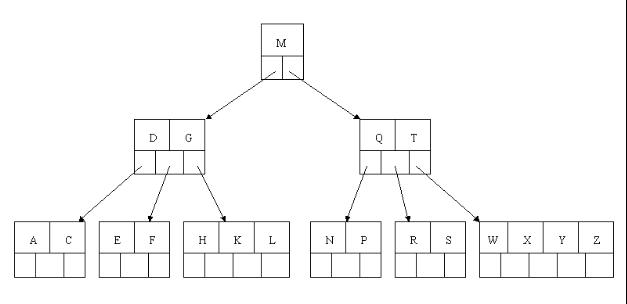
6.2、删除(delete)操作
（1）删除操作的两个步骤
   　第一步骤：在树中查找被删关键字K所在的地点
    　第二步骤：进行删去K的操作

（2）删去K的操作
    　B-树是二叉排序树的推广，中序遍历B-树同样可得到关键字的有序序列（具体遍历算法【参见练习】）。任一关键字K的中序前趋(后继)必是K的左子树(右子树)中最右(左)下的结点中最后(最前)一个关键字。
    　若被删关键字K所在的结点非树叶，则用K的中序前趋(或后继)K'取代K，然后从叶子中删去K'。从叶子*x开始删去某关键字K的三种情形为：
    　情形一：若x->keynum>Min，则只需删去K及其右指针(*x是叶子，K的右指针为空)即可使删除操作结束。
  注意：
    　
    　情形二：若x->keynum=Min，该叶子中的关键字个数已是最小值，删K及其右指针后会破坏B-树的性质(3)。若*x的左(或右)邻兄弟结点*y中的关键字数目大于Min，则将*y中的最大(或最小)关键字上移至双亲结点*parent中，而将*parent中相应的关键字下移至x中。显然这种移动使得双亲中关键字数目不变；*y被移出一个关键字，故其keynum减1，因它原大于Min，故减少1个关键字后keynum仍大于等于 Min；而*x中已移入一个关键字，故删K后*x中仍有Min个关键字。涉及移动关键字的三个结点均满足B-树的性质(3)。请读者验证，上述操作后仍满足B-树的性质(1)。移动完成后，删除过程亦结束。
    　情形三：若*x及其相邻的左右兄弟(也可能只有一个兄弟)中的关键字数目均为最小值Min，则上述的移动操作就不奏效，此时须*x和左或右兄弟合并。不妨设*x有右邻兄弟*y(对左邻兄弟的讨论与此类似)，在*x中删去K后，将双亲结点*parent中介于*x和*y之间的关键字K，作为中间关键字，与并x和*y中的关键字一起"合并"为一个新的结点取代*x和*y。因为*x和*y原各有Min个关键字，从双亲中移人的K'抵消了从*x中删除的K，故新结点中恰有2Min(即2「m/2」-2≤m-1)个关键字，没有破坏B-树的性质(3)。但由于K'从双亲中移到新结点后，相当于从*parent中删去了K'，若parent->keynum原大于Min，则删除操作到此结束；否则，同样要通过移动*parent的左右兄弟中的关键字或将*parent与其左右兄弟合并的方法来维护B-树性质。最坏情况下，合并操作会向上传播至根，当根中只有一个关键字时，合并操作将会使根结点及其两个孩子合并成一个新的根，从而使整棵树的高度减少一层。

    　

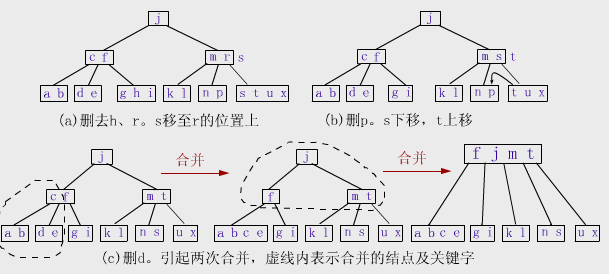
分析：
　   第1个被删的关键字h是在叶子中，且该叶子的keynum>Min(5阶B-树的Min=2)，故直接删去即可。第2个删去的r不在叶子中，故用中序后继s取代r，即把s复制到r的位置上，然后从叶子中删去s。第3个删去的p所在的叶子中的关键字数目是最小值Min，但其右兄弟的 keynum>Min，故可以通过左移，将双亲中的s移到p所在的结点，而将右兄弟中最小(即最左边)的关键字t上移至双亲取代s。当删去d时，d 所在的结点及其左右兄弟均无多余的关键字，故需将删去d后的结点与这两个兄弟中的一个(图中是选择左兄弟(ab))及其双亲中分隔这两个被合并结点的关键字c合并在一起形成一个新结点(abce)。但因为双亲中失去c后keynum<Min，故必须对该结点做调整操作，此时它只有一个右兄弟，且右兄弟无多余的关键字，不可能通过移动关键字来解决。因此引起再次合并，因根只有一个关键字，故合并后树高度减少一层，从而得到上图的最后一个图。

    　B-树上操作的时间通常由存取磁盘的时间和CPU计算时间这两部分构成。B-树上大部分基本操作所需访问盘的次数均取决于树高h。关键字总数相同的情况下B-树的高度越小，磁盘I/O所花的时间越少。
    　与高速的CPU计算相比，磁盘I/O要慢得多，所以有时忽略CPU的计算时间，只分析算法所需的磁盘访问次数（磁盘访问次数乘以一次读写盘的平均时间(每次读写的时间略有差别)就是磁盘I/O的总时间）。

1、B-树的高度
    　定理9.1 若n≥1，m≥3，则对任意一棵具有n个关键字的m阶B-树，其树高h至多为：
        log_t((n+1)/2)+1。
这里t是每个(除根外)内部结点的最小度数，即

    　由上述定理可知：B-树的高度为O(logtn)。于是在B-树上查找、插入和删除的读写盘的次数为O(log_tn)，CPU计算时间为O(mlog_tn)。

2、性能分析
　　①n个结点的平衡的二叉排序的高度H（即lgn）比B-树的高度h约大lgt倍。
    　【例】若m=1024，则lgt=lg512=9。此时若B-树高度为4，则平衡的二叉排序树的高度约为36。显然，若m越大，则B-树高度越小。
　　②若要作为内存中的查找表，B-树却不一定比平衡的二叉排序树好，尤其当m较大时更是如此。
    　因为查找等操作的CPU计算时间在B-树上是
        O(mlog_tn)=0(lgn·(m/lgt))
而m/lgt>1，所以m较大时O(mlogtn)比平衡的二叉排序树上相应操作的时间O(lgn)大得多。因此，仅在内存中使用的B-树必须取较小的m。（通常取最小值m=3，此时B-树中每个内部结点可以有2或3个孩子，这种3阶的B-树称为2-3树）。

B+树

       B+树是B-树的变体，也是一种多路搜索树：

       1.其定义基本与B-树同，除了：

       2.非叶子结点的子树指针与关键字个数相同；

       3.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；

       5.为所有叶子结点增加一个链指针；

       6.所有关键字都在叶子结点出现；

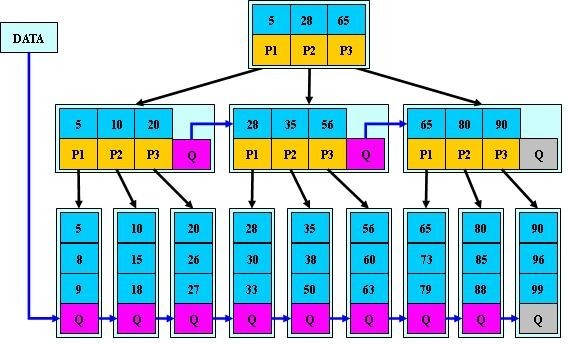
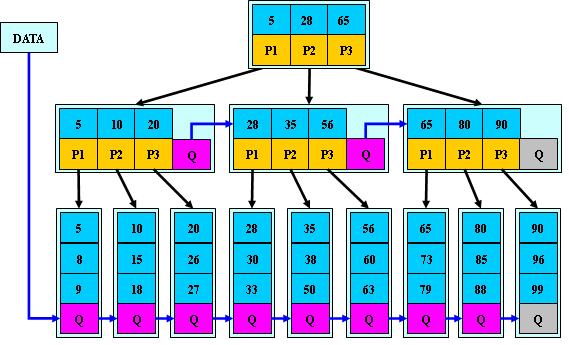
       如：（M=3）

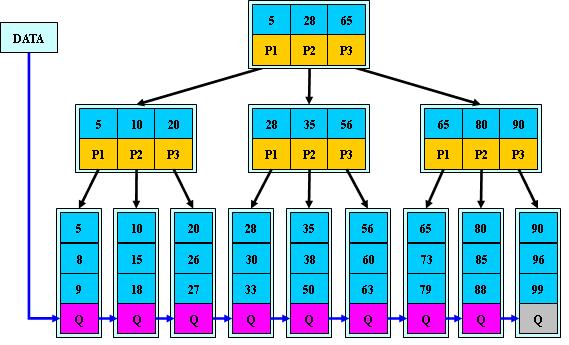
B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；
       B+的特性：

       1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；

       2.不可能在非叶子结点命中；

       3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；

       4.更适合文件索引系统；

B*树

       是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；

B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）；
       B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

       B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

       所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

【摘要】

红黑树（原文链接http://www.cnblogs.com/fornever/archive/2011/12/02/2270692.html）

B树（http://blog.csdn.net/liuxincumt/article/details/7469920）

posted @ 2016-03-25 12:18 cancanw 阅读(2528) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

cancanw

数据结构--树（遍历，红黑，B树）

B树的高度

公告