熵、信息增益以及其他

　　很长一段时间，都对熵、信息增益懵懵懂懂，一知半解。最近，正巧碰到研究决策树算法，于是乎，恶补了这方面的知识。

　　1.什么是熵（Entropy）

　　在信息论里面，熵是对不确定性的测量，熵越高，则能传输越多的信息，熵越低，则意味着传输的信息越少。熵度衡量了系统的不确定性，当我们缺乏对某个系统的知识，其不确定性也随着增加。

　　例如抛硬币，在理想情况下他们无法预测出现的是正面还是反面，此时熵达到最大。但是对于“明天太阳从东方升起”，我们完全可以依靠目前的知识，预测该事件肯定会发生，信息熵最小。

　　香农给出了熵数学表达：某个事件用随机变量X表示，其可以的取值{x₁, x₂, ...x_n }，则该事件的信息熵定义为，

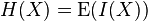
　　其中I(X)，表示随机变量的信息，I(X)一般定义为：

　　那么，熵的定义为：

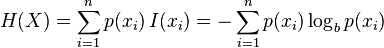
　　下图给出了二分类问题熵函数：

　　以上给出的是单变量的信息熵，我们还可以简单推导出两个随机变量X和Y联合信息熵：

　　相应的，条件熵定义为：

 

　　2.什么是信息增益（Information Gain）

　　在介绍完基本概率，下面将介绍信息增益。信息增益，是一种衡量样本特征重要性的方法，直观的理解是有无样本特征对分类问题的影响的大小。假设某个状态下系统的信息熵为H(Y)，再引入某个特征X后的信息熵为H(Y|X)，则特征X的信息增益定义为：

	特征A	特征B	特征C	类别
samp1	0	1	0	0
samp2	0	0	1	0
samp3	1	0	0	1
samp4	1	0	1	1

 

　　H(Y)表示整个系统的信息量：

    　　 

　　H(Y|A)表示“看到”（已知）特征A的信息量：

    

 

　　以此类推，可以求出H(Y|B):

　

　　H(Y|C):

　　

　　于是，三个特征在当前系统下信息增益得分排序：A> B> C，利用信息增益我们完成了对特征重要性的排序，可以用于特征选择、决策树分裂是选择特征的依据等。

　　3.其他

　　在文本选择一文中，我们展开了某个特征的信息增益表达公式：

　　其中等号右边第一行，表示H(Y)信息熵，而等号右边第二行表示H(Y|X=t_i)信息熵（利用条件熵表达式右边等号第二行展开）。