线性回归模型之一

　　本节开始介绍第一个机器学习模型：线性回归模型（Linear Regression Model)。线性回归的目的是预测连续变量的值，比如股票走势，房屋的价格预测。从某种程度上说，线性回归模型，就是函数拟合。而线性回归，针对线性模型拟合，是回归模型当中最简单一种。形式化描述回归模型：对于给定的训练样本集包含N个训练样本{x⁽ⁱ⁾} 相应的目标值{t⁽ⁱ⁾}}(i=1,2,....N)，我们的目的是给定一个新样本x 预测其值 t，注意与分类问题不同是{t⁽ⁱ⁾}属于连续变量。

　　

　　最简单的线性回归模型：

                                                                          (1)

其中，x={x₁,x₂,x₃,...x_D}，D个特征项，w={w₁,w₂,w₃...w_D}，被称为参数或者权重。线性回归模型的关系是求出w 。

上面的公式可以简化为：

                                                                                  (2)   

其中Φ_j(x)被成为集函数，令Φ₀(x)=1，则上式又可以写成：

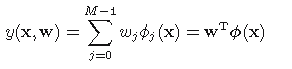　　　　　　　　                                                           (3)                          

集函数的一般有多项式集函数，比如Gaussian集函数，Sigmoidal集函数。为方便出公式推导，我们假设：

最简单的集函数形式：Φ_j(x) = xj

　　为了求出模型参数（一旦w 求出，模型就被确定），我们首先需要定义出错误函数或者（error function)或者又被成为损失函数（cost function)，优化损失函数的过程便是模型求解的过程。

我们定义线性回归模型的损失函数：

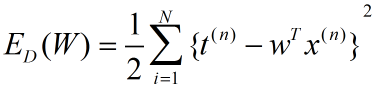                                                                    (4)

优化当前函数有很多方便，包括随机梯度下降算法（gradient descent algorithm）算法步骤如下：

　　1)随机起始参数W;

      2)按照梯度反方向更新参数W直到函数收敛。

算法公式表示：

                                                                                          (5)

其中，η表示学习速率(learning rate)。倒三角表示对损失函数求导，得到导数方向。对公式(4)求导后：

                                          (6)

　　公式（5）更新方法又被称为批梯度下降算法(batch gradient descent algorithm），每更新一次W需要遍历所有的训练样本，当样本量很大是，将会是非常耗时的。另一种更新方法，随机梯度下降的算法，每次碰到一个样本，即对W进行更新：

                                                          (7) 

随机梯度算法速度要远于批更新，但可能会得到局部最优解。需要注意的是，在随机梯度下降方法中，并不是每一次更新都判断算法何时收敛，而是在m次的更新后再做判断（往往m<样本数量）。