<算法图解>读书笔记:第3章 递归
第3章 递归
3.1 递归
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
来自<百度百科>
- 如果使用循环,程序的性能可能更高;如果使用递归,程序可能更容易理解
3.2 基线条件和递归条件
- 每个递归函数都有两部分:基线条件(base case)和递归条件( recursive case).递归条件指函数调用自己,而基线条件指函数不再调用自己,从而避免形成无限循环
3.3 栈
栈(stack)又名堆栈,它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
来自<百度百科>
3.3.1 调用栈
调用栈(英语:Call stack,英文直接简称为“栈”(the stack))别称有:执行栈(execution stack)、控制栈(control stack)、运行时栈(run-time stack)与机器栈(machine stack),是计算机科学中存储有关正在运行的子程序的消息的栈。有时仅称“栈”,但栈中不一定仅存储子程序消息。几乎所有计算机程序都依赖于调用栈,然而高级语言一般将调用栈的细节隐藏至后台。
来自<百度百科>
- 当函数fn1调用另一个函数fn2时,当fn1暂停并处于未完成状态,fn1的所有变量的值都还在内存中.当fn2执行结束后,回到fn1,并从离开的地方开始接着往下执行
3.3.2 递归调用栈
-
计算阶乘的递归函数
def fact(x): if x == 1: return 1 else: return x * fact(x-1) print(fact(3))这个程序运行时栈的变化如下
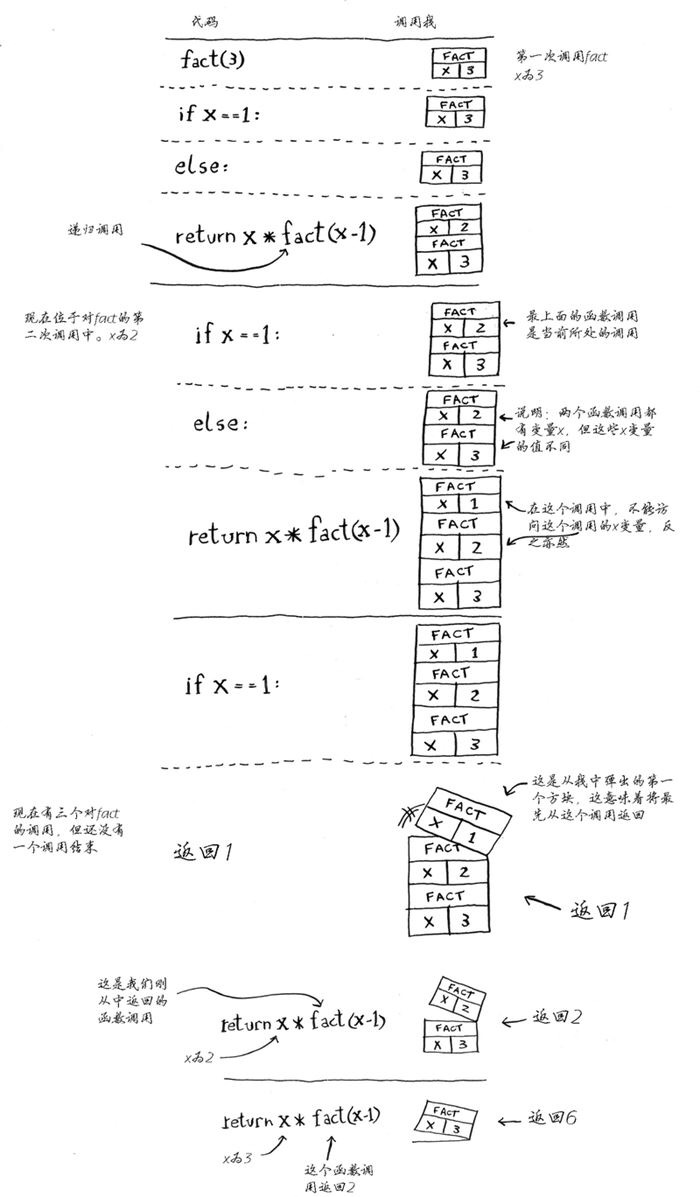
)
- 使用栈虽然很方便,但也要付出代价:存储详尽的信息可能占用大量的内存.每个函数调用都要占用一定的内存,如果栈很高,就意味着计算机存储了大量函数调用的信息,在这种情况下,有两种选择:
- 重新编写代码,战而使用循环
- 使用尾递归.这是一种高级递归主题,并非所有语言都支持
3.4 小结
- 递归指的是调用自己的函数
- 每个递归函数都有两个条件:基线条件和递归条件
- 栈有两种操作:压入(插入)和弹出(删除并读取)
- 所有的函数调用都进入调用栈
- 调用栈可能很长,这将占用大量内存



