<算法图解>读书笔记:第1章 算法简介

阅读书籍:[美]Aditya Bhargava◎著 袁国忠◎译.人民邮电出版社.《算法图解》

第1章 算法简介

1.2 二分查找

• 一般而言,对于包含n个元素的列表,用二分查找最多需要\(log_2n\)步,而简单查找最多需要n步

• 仅当列表是有序的时候,二分查找才管用

• python猜数字代码(二分查找)

  def binarySeach (list,item):
      low = 0
      high = len(list) - 1    
      while low <= high:
          mid = (low + high) // 2
          guess = list[mid]
          if guess == item:
              return mid
          if guess > item:
              high = mid - 1
          else:
              low = mid + 1
      return None
  
  myList = [1,3,5,7,9,11,13]
  print(binarySeach(myList,5))
  print(binarySeach(myList,-1))   
  

• 一般而言,应选择效率高的算法,以最大限度地减少运行时间或占用空间

• 线性时间

  在计算复杂性理论,一个被称为线性时间或 Ο（n）时间的算法，表示此算法解题所需时间正比于输入资料的大小，通常以n表示。换句话说，执行时间与输入资料大小为线性比例。例如将一列数字加总的所需时间，正比于串行的长度。
  来自<百度百科>

• 对数时间 : 二分查找的运行时间

1.3 大O表示法

• 大O表示法是一种特殊的表示法,指出了算法的速度有多快

  大O表示法：算法的时间复杂度通常用大O符号表述，定义为\(T_{[n]} = O_{(f(n))}\)。称函数T(n)以f(n)为界或者称T(n)受限于f(n)。 如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)。T(n)称为这一算法的“时间复杂度”。当输入量n逐渐加大时，时间复杂度的极限情形称为算法的“渐近时间复杂度”。
  来自<百度百科>

• 仅知道算法需要多长时间才能运行完毕还不够,还需知道运行时间如何随列表而增加.这正是大O表示法的用武之地
• 大O表示法能够比较操作数,它指出了算法运行时间的增速
• 大O表示法说的是最糟的情况.选择算法时,除考虑最糟情况下的运行时间外,还应考虑平均情况下的运行时间
• 一些常见的大O运行时间
  • \(O _{(logn)}\),也叫对数时间,这样的算法包括二分查找
  • \(O _{(n)}\),也叫线性时间,这样的的算法包括简单查找
  • \(O _{(n^*logn)}\),这样算法包括快速排序(一种较快的排序算法)
  • \(O _{(n^2)}\),这样的算法包括选择排序(一种速度较慢的排序算法)
  • \(O _{(n!)}\),也叫阶乘时间
• 从快到慢的顺序:
  
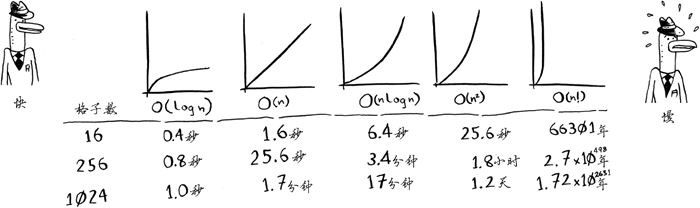
  • 算法的速度指的并非时间,而是操作数的增速
  • 谈论算法的速度时,我们说的是随着输入的增加,其运行将以什么样的速度增加
  • 算法的运行时间用大O表示法表示
  • \(O _{(logn)}\)比\(O _{(n)}\)快,当需要搜素的元素越多时,前者比后者快得越多

1.3.5 旅行商

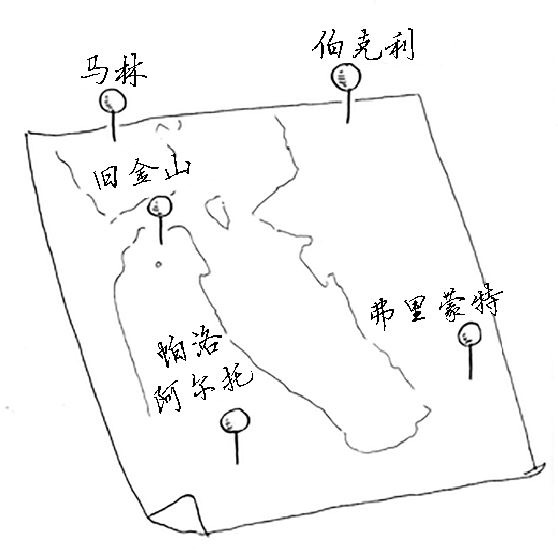
• 一位旅行商要前往这5个城市,同时要确保旅程最短,为此要考虑前往这些城市的各种可能.5个城市有120种不同的排列方式.推而广之,涉及n个城市,需要执行n!(n的阶乘)次操作才能计算出结果,因此运行时间为\(O _{(n!)}\).这种算法很槽糕,可别无选择.

1.4 小结

• 二分查找的速度比简单查找快得多
• 算法运行时间并不以秒为单位,是从其增速的角度度量的,用大O表示法表示