Redis设计与实现-5.整数集合和压缩列表

整数集合

       整数集合（intset）是集合键的底层实现之一，当一个集合只包含 整数值元素，并且这个集合的元素数量不多时，Redis就会使用郑书记和作为集合键的底层实现。

整数集合的实现

     整数集合是redis用于保存整数值的集合抽象数据结构，它可以可以保存类型位int16_t、int32_t、int64_t的整数值，并且保证集合中不会出现重复元素。

intset.h/intset结构表示一个整数集合

typedef struct intset {
    uint32_t encoding;//编码方式
    uint32_t length;//集合包含的元素数量
    int8_t contents[];//保存元素的数组
} intset;

contents数组是整数集合的底层实现：整数集合的每个元素都是contents数组的一个数组项，各个项在数组中按值的大小从小到大有序地排列，并且数组中不包含任何重复项。

       length属性记录了整数集合包含的元素数量，也即是contents数组的长度。

       虽然intset结构将contents属性声明为int8 t类型的数组，但实际上contents数组真正类型取决于encoding属性的值：

 

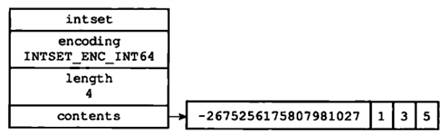
       上图中，contents数组保存的四个整数值中，只有-2675256175807981027是真正需要用int64_t类型来保存的，而其他的1、3、5三个值都可以用int16_t类型来保存，不过根据整数集合的升级规则，当想一个底层为int16_t数组的整数集合添加一个int64_t类型的整数值时，整数集合已有的所有元素都会被转换成int64_t类型。

升级

       每当我们要讲一个新元素添加到整数集合里面，并且新元素的类型比整数集合现有元素类型长时，整数集合都需要先进行升级（upgrade），然后才能将新元素添加到整数集合里面。

       升级整数集合并添加新元素共分为三步进行：

1 根据新元素的类型，扩张整数集合底层数组的空间大小，并为新元素分配空间。

2 将底层数组现有的所有元素都转换成与新元素相同的类型，并将类型转换后的元素继续放置到正确的位上，而且在放置元素的过程中，需要继续维持底层数组的有序性质不变。

3 将新元素添加到底层数组里面

       因为每次想整数集合添加新元素都可能引起升级，而每次升级都需要对底层数组中已有的所有元素进行类型转换，所以想整数集合添加新元素的时间复杂度为O(N)。

       因为引发升级的新元素的长度总是比整数集合现有的所有元素长度都大，所以这个新元素的值要么大于所有现有元素，要么小于所有现有元素。

升级的好处

       整数集合的升级策略有两个好处，一个是提升整数集合的灵活性，另一个是尽可能地节约内存。

提升灵活性

       因为C语言是静态类型语言，为了避免类型错误，我们通常不会讲两种不同类型的值放在同一个数据结构里面。

       但是，因为整数集合可以通过自动升级底层数组来适应新元素，所以我们可以随意地将int16_t、int32_t、int64_t类型的整数添加到集合中，而不必担心出现类型错误。

降级

       整数集合不支持降级操作，一旦对数组进行了升级，编码就会一直保持升级后的状态。

压缩列表

       压缩列表（ziplist）是列表键和哈希键的底层实现之一。当一个列表键只包含少量列表项，并且每个列表项要么是小整数值，要么是长度比较短的字符串，那么redis就会使用压缩列表来作为列表键的底层实现。

       另外，当一个哈希键只包含少量键值对，并且每个键值对的键和值要么是小整数值，要么是长度比较短的字符串，那么redis就会使用压缩列表来做哈希键的底层实现。

举个栗子，执行以下命令

127.0.0.1:6379> hmset profile “name” “jack“ “age” 28 
ok
127.0.0.1:6379> object encoding profile
"ziplist"

压缩列表的构成

       压缩列表是redis为了节约内存而开发的，是由一系列特殊编码的连续内存块组成的顺序型数据结构。一个压缩表可以包含任意多个节点（entry），每个节点可以保存一个字节数组或者一个整数值。

下图展示了压缩列表的各个组成部分：

 

以下为各个组成部分的作用

 

下图展示了一个压缩列表示例：

1 列表zlbytes属性值为0x50（十进制80），表示压缩列表总长80字节。

2 libzltail属性的值为0x3c（十进制60），这表示如果我们有一个指向压缩列表起始地址的指针p，那么只要用指针p加上偏移量60，就可以计算出表尾节点entry3的地址。

3 列表zllen属性的值为0x3（十进制3），表示压缩列表包含三个节点。

压缩列表节点的构成

       每个压缩列表节点可以保存一个字节数组或者一个整数值，其中，字节数组可以是一下三种长度的其中一种：

1 长度小于等于63（2^6-1）字节的字节数组

2 长度小于等于16383（2^14-1）字节的字节数组

3 长度小于等于4294967295（2^32-1）字节的字节数组

而整数值则可以是以下六种长度的其中一种

1 4位长，介于0至12之间的无符号整数

2 1季节长的有符号整数

3 3字节长的有符号整数

4 int16_t类型整数

5 int32_t类型整数

6 int64_t类型整数

每个压缩列表节点都由previous_entry_length、encoding、content三个部分组成，如下图

 

我们分别介绍这三部分

previous_entry_length

       节点的previous_entry_length属性以字节为单位，记录了压缩列表中前一个节点的长度。previous_entry_length属性的长度可以使1字节或者5字节：

1 如果前一节点的长度小于254字节，那么previous_entry_length属性的长度为1字节：前一节点的长度就保存在这一字节里面。

2 如果前一节点的长度大于等于254字节，那么previous_entry_length属性的长度为5字节：其中属性的第一个字节会被设置为0xFE（十进制值254），而之后的四个字接则用于保存前一节点的长度。

这两种情况如下图

 

       因为节点的previous_entry_length属性记录了前一个节点的长度，所以程序可以通过指针运算，根据当前节点的起始地址来计算出前一个节点的起始地址。

       压缩列表的从表尾向表头遍历操作就是使用这一原理实现的，只要我们拥有了一个指向某个节点起始地址的指针，程序就可以一直向前一个节点回溯，最终到达压缩列表的表头节点。

encoding

       节点的encoding属性记录了节点的content属性所保存数据类型以及长度：

1 一字节、两字节或者五字节长，值的最高位为00、01或者10的是字节数组编码：这种编码表示节点的content属性保存着字节数组，数组的长度由编码除去最高两位之后的其他位记录。

2 一字节长，值的最高位以11开头的是整数编码：这种编码表示节点的content属性保存着整数值，整数值的类型和长度由编码出去最高两位之后的其他位记录。

       下表中的下划线“_”表示留空，而b、x等变量则代表实际的二进制数据，多个字节之间用空格隔开。

 

content

       节点的content属性负责保存节点的值，节点值可以是一个字节数组或者整数，值的类型和长度由节点的encoding属性决定。

图7-9展示了一个保存字节数组的节点示例：

1 编码的最高两位00表示节点保存的是一个字节数组

2 编码的后两位001011记录了字节数组的长度11

3 content属性保存着节点的值“hello world”

 

图7-10展示了一个保存整数值的节点示例：

1 编码11000000表示节点保存的是一个int16_t类型的整数值

2 content属性保存着节点的值10086

连锁更新

       前面说过，每个节点的previous_entry_length属性都记录了前一个节点的长度：如果前一节点的长度小于254字节，那么previous_entry_length属性的长度为1字节，前一节点的长度就保存在这一字节里面。

       现在，考虑这样一种情况：在一个压缩列表中，有多个连续的，长度介于250字节到253字节之间的节点e1至eN。

       以为e1至eN的所有节点的长度都小于254字节，所以记录这些节点的长度只需要1字节长的previous_entry_length属性。

       这时，如果我们将一个长度大于等于254字节的新节点new 设置为压缩列表的表头节点，如下图

 

       因为e1的previous_entry_length属性仅长1字节，它没办法保存新节点new的长度，所以程序将对压缩列表执行空间重分配操作，并将e1节点的previous_entry_length属性从原来的1字节长扩展为5字节长。

       现在，麻烦的事情来了，e1原本的长度介于250字节至253字节之间，在为previous_entry_length属性新增4个字节的空间之后，e1的长度就变成了介于254字节至257字节之间，而这种长度使用1字节长的previous_entry_length属性是没办法保存的。

       因为，为了让e2的previous_entry_length属性可以记录下e1的长度，程序需要再次对压缩列表执行空间重分配操作，并将e2节点的previous_entry_length属性从原来的1字节长扩展为5字节长。

       如此循环，程序需要不断地对压缩列表执行空间重分配操作，直到eN为止。

       redis将这种特殊情况下产生的连续多次空间扩展操作称之为“连锁更新”（cascade update）。除了添加新节点可能会引发连锁更新外，删除节点也可能会引发连锁更新。

       因为连锁更新在最坏情况下需要对压缩列表执行n次空间重分配操作，而每次空间重分配的最坏复杂度为O(N),所以连锁更新的最坏复杂度为O(N^2)。

       要注意的是，尽管连锁更新的复杂度较高，但它真正造成性能问题的几率是很低的

1 压缩列表要恰好有多个连续的、长度介于250-253字节之间的节点，连锁更新才有可能被引发。

2 即使出现连锁更新，只要被更新的节点数量不多，就不会对性能造成影响。

       因此，ziplistpush等命令的平均复杂度仅为O（n），实际使用中，我们可以放心地使用这些函数，而不必担心连锁更新会影响压缩列表性能。