manim边学边做--移动动画
在Manim中,其实直线移动的动画非常简单,每个Mobject对象都有animate属性,
通过obj.animate.shift()或者obj.animate.move_to()很容易将对象从一个位置移往另一个位置。
不过,如果要更复杂的移动路线,那么animate属性的移动方法就无法满足了。
本篇介绍Manim中的两个处理复杂移动动画的类MoveAlongPath和PhaseFlow。
MoveAlongPath能使图形对象沿着指定路径(如贝塞尔曲线等)移动,并且可精细调节运动参数。
而且它易于和其他动画组合,主要用于动画制作、路径演示和物理轨迹模拟等场景的动画类。
PhaseFlow是一个基于向量场和微分方程,通过数值计算求解轨迹的移动动画。
它可以展示相空间中系统状态动态演化过程,多用在物理系统模拟、控制系统分析和生物系统建模等领域。
1. 动画概述
1.1. MoveAlongPath
MoveAlongPath 的核心特点是能让一个 Mobject(manim 中的图形对象)沿着指定的路径进行移动。
这个路径可以是通过各种方式定义的,比如使用贝塞尔曲线、折线等。
比如,你可以定义一个复杂的二次贝塞尔曲线作为路径,然后让一个圆形 Mobject 沿着这条曲线运动。
此外,它还允许你对运动的参数进行精细控制,可以设置运动的速度,通过改变速度参数来实现匀速运动或者变速运动。
比如,你可以让一个对象开始运动较慢,然后逐渐加速沿着路径前进,还可以指定运动的起始点和结束点在路径上的位置,这样就能灵活地控制对象在路径的哪一段进行运动。
最后,MoveAlongPath 可以很方便地与其他动画效果组合使用。
比如,在对象沿着路径运动的同时,可以结合旋转动画,让对象在移动过程中自身还进行旋转,从而创造出更加复杂和生动的动画效果。
它的参数主要有:
| 参数名称 | 类型 | 说明 |
|---|---|---|
| mobject | Mobject | 要移动的Mobject对象 |
| path | VMobject | 指定移动的路径 |
| suspend_mobject_updating | bool | 控制是否暂停mobject的更新 |
suspend_mobject_updating参数如果为True,则在动画插值过程中暂停mobject的更新;
如果为False,则继续更新。
1.2. PhaseFlow
PhaseFlow 是和动力系统紧密相关的动画效果类。
它是基于向量场来工作的,这个向量场通常是由一个或多个微分方程定义的。
比如,对于一个简单的二维动力系统,可能有$ \frac{dx}{dt}=f(x,y) \(和\) \frac{dy}{dt}=g(x,y) $这样的微分方程组来定义向量场,PhaseFlow 会根据这些方程计算相空间中的轨迹。
PhaseFlow 主要用于展示相空间(Phase Space)中系统状态的动态演化过程。
相空间是一个抽象的空间,其坐标轴可以代表系统的状态变量(如位置、速度等)。
PhaseFlow 能够以动画的形式展示从不同初始状态出发的轨迹是如何在相空间中随着时间流动的,并且这种展示是连续而平滑的。
它的参数主要有:
| 参数名称 | 类型 | 说明 |
|---|---|---|
| mobject | Mobject | 要移动的Mobject对象 |
| function | func | 定义相流的动态行为 |
| virtual_time | float | 虚拟时间,用于在计算相流轨迹时确定时间步长等相关计算 |
| suspend_mobject_updating | bool | 控制是否暂停mobject的更新 |
| rate_func | func | 控制动画的速率 |
function参数通常基于给定的微分方程来计算相空间中的轨迹变化。
2. 使用示例
下面通过示例来演示MoveAlongPath和PhaseFlow的应用场景。
示例中的应用场景是简化之后的,目的是演示MoveAlongPath和PhaseFlow的使用方式。
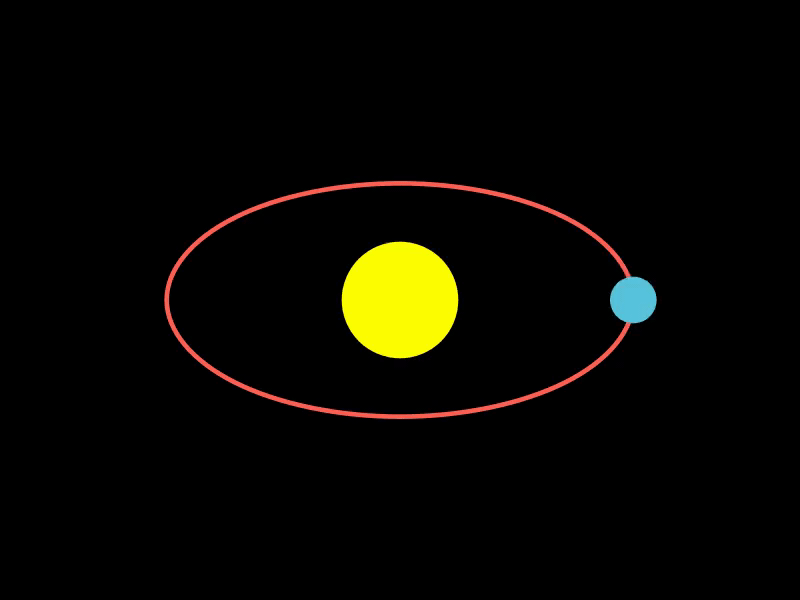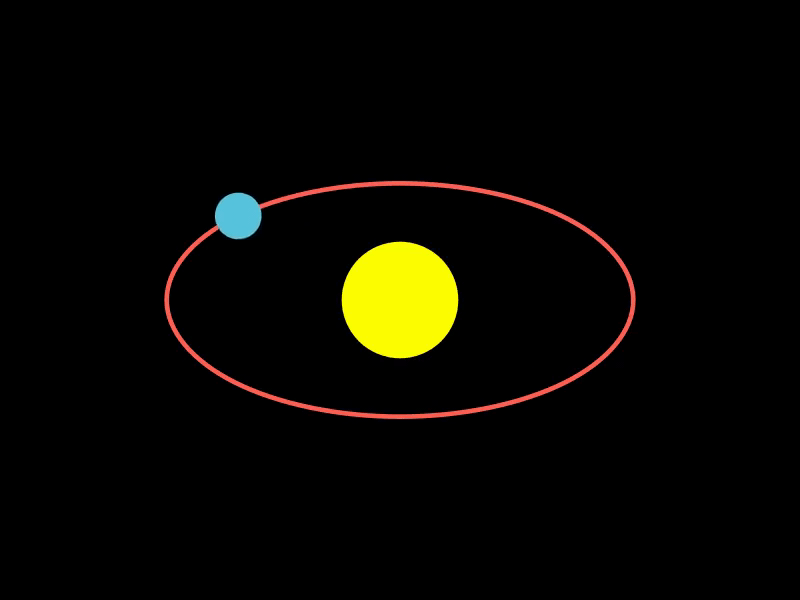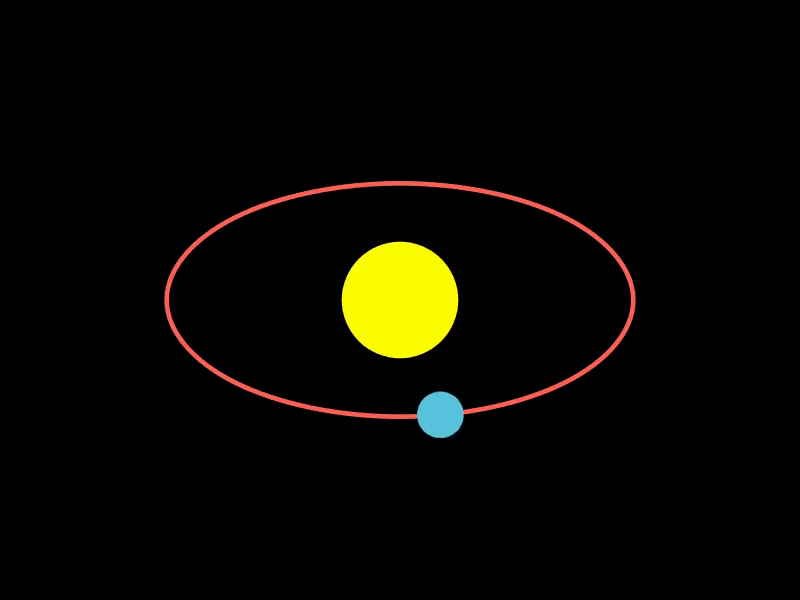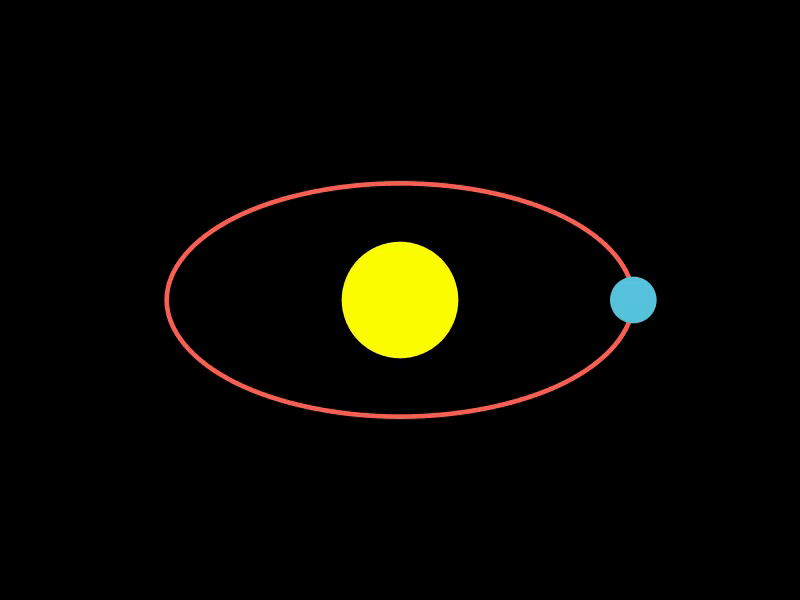
2.1. 模拟行星绕太阳公转
该示例使用MoveAlongPath创建了一个行星绕太阳公转的动画,通过定义椭圆轨道路径,让行星沿着该路径运动,模拟了天体运动场景。
# 创建太阳
sun = Dot(color=YELLOW, radius=0.5)
# 创建椭圆轨道
orbit_path = Ellipse(width=4, height=2)
# 创建行星
planet = Dot(color=BLUE, radius=0.2)
self.add(sun, orbit_path, planet)
# 让行星沿着椭圆轨道运动
self.play(
MoveAlongPath(planet, orbit_path),
run_time=5,
rate_func=linear,
)
2.2. 展示函数曲线绘制过程
这个示例利用MoveAlongPath展示了函数曲线的绘制过程,通过沿着定义好的函数曲线路径移动一个点,帮助理解函数的形状。
# 定义函数(这里以y = x^2为例)
def f(x):
return x**2
graph = axes.plot(
f,
x_range=[-2.5, 2.6],
color=GREEN,
stroke_width=2,
)
self.play(Create(graph))
# 创建一个点沿着曲线运动
moving_dot = Dot(color=YELLOW)
self.play(
MoveAlongPath(moving_dot, graph),
run_time=5,
rate_func=linear,
)
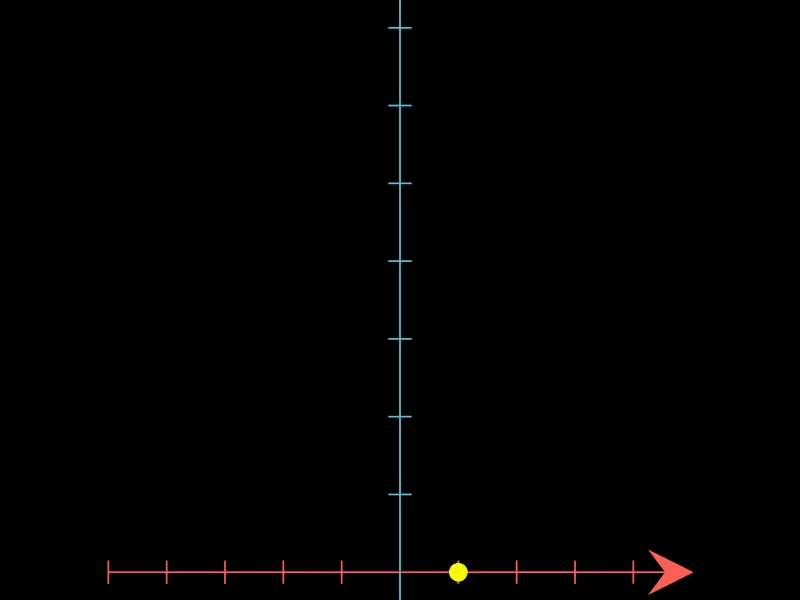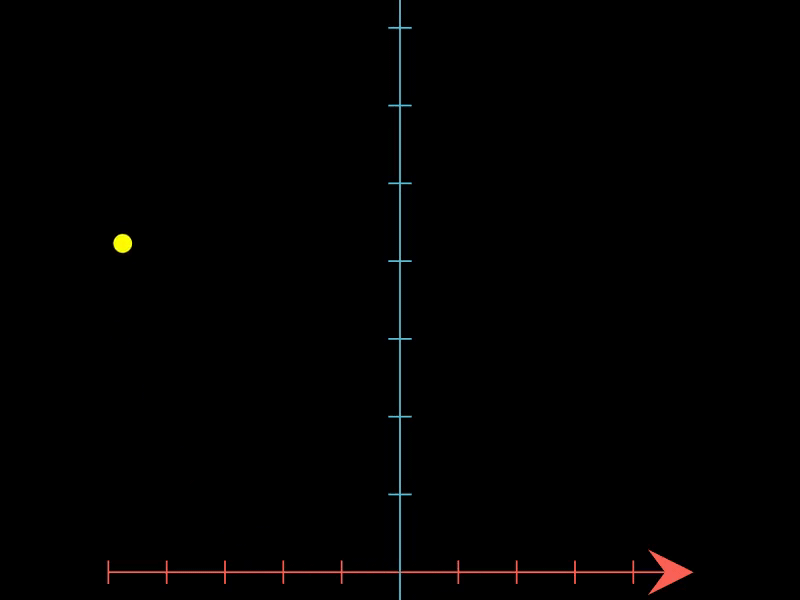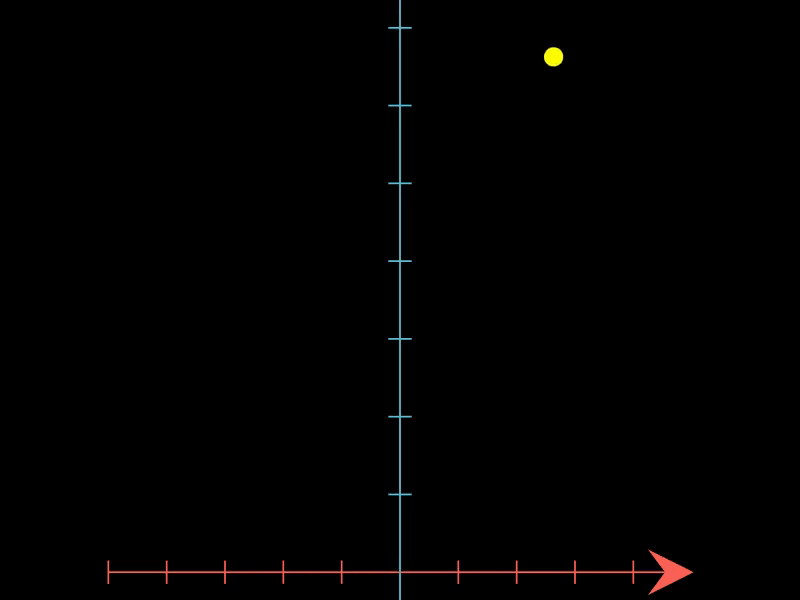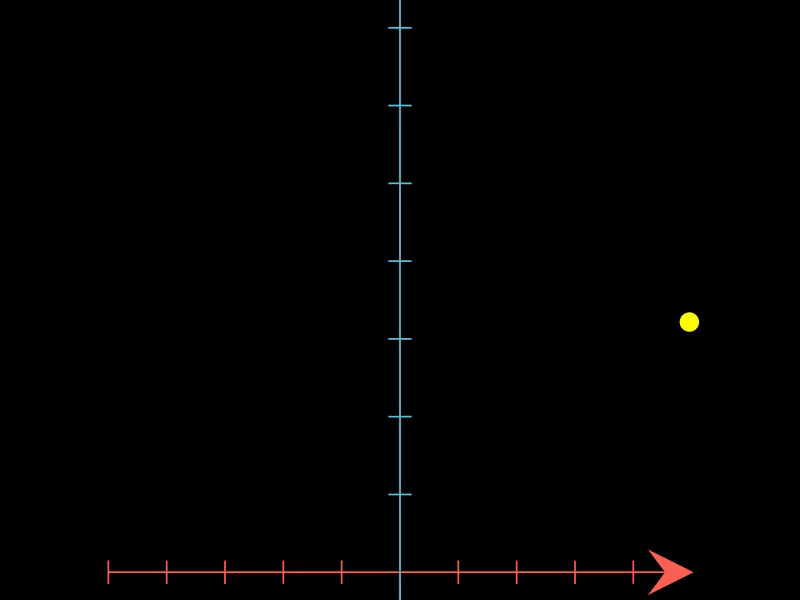
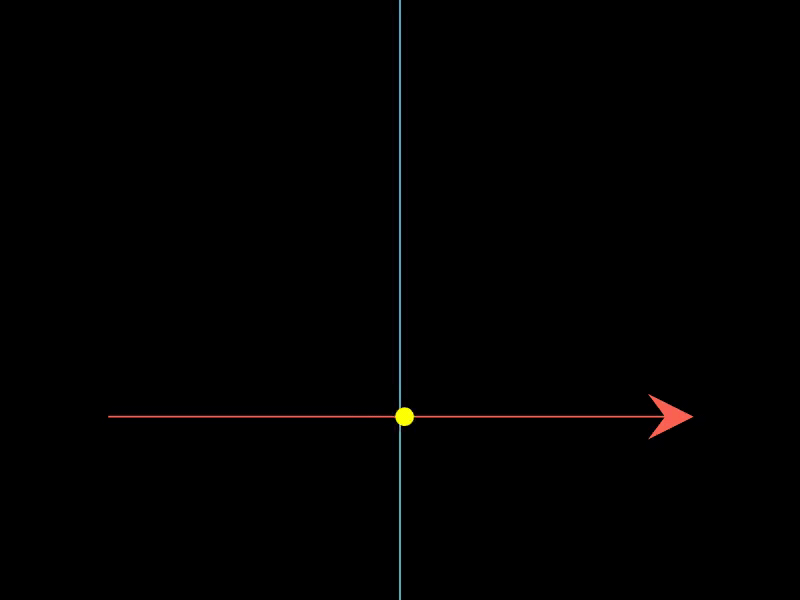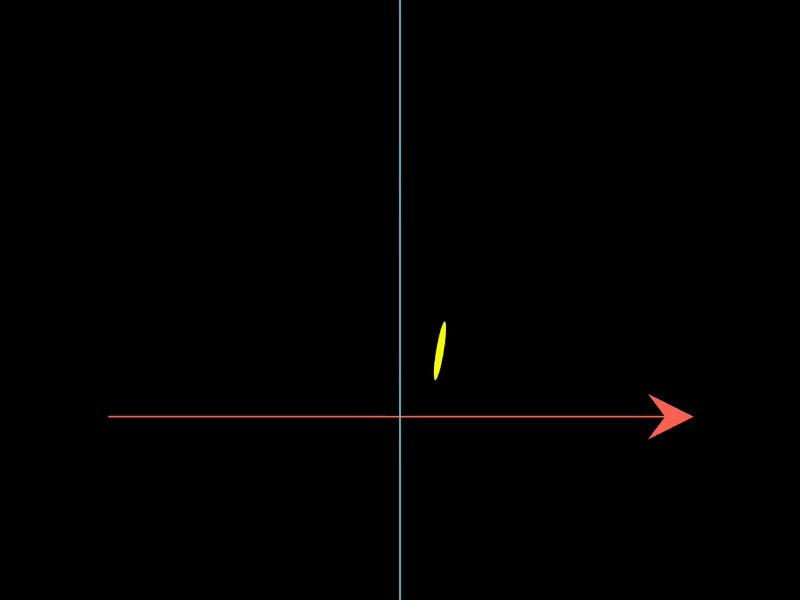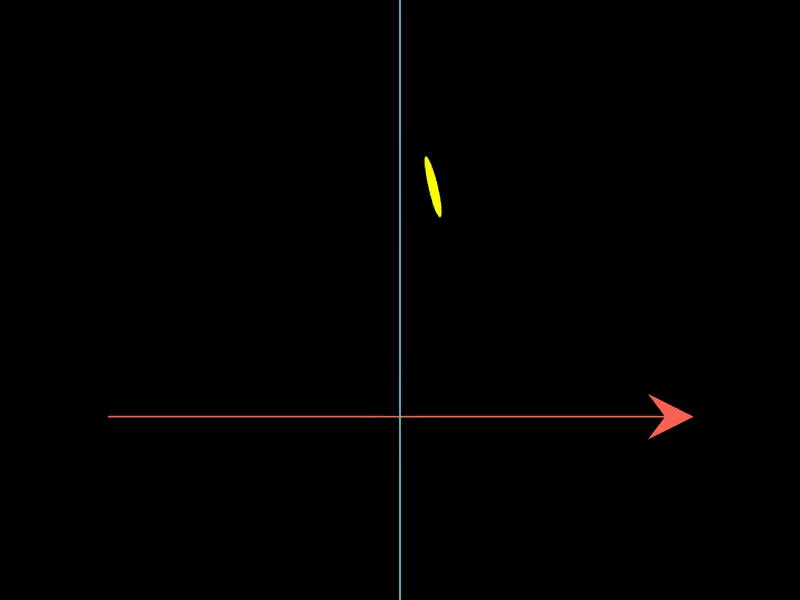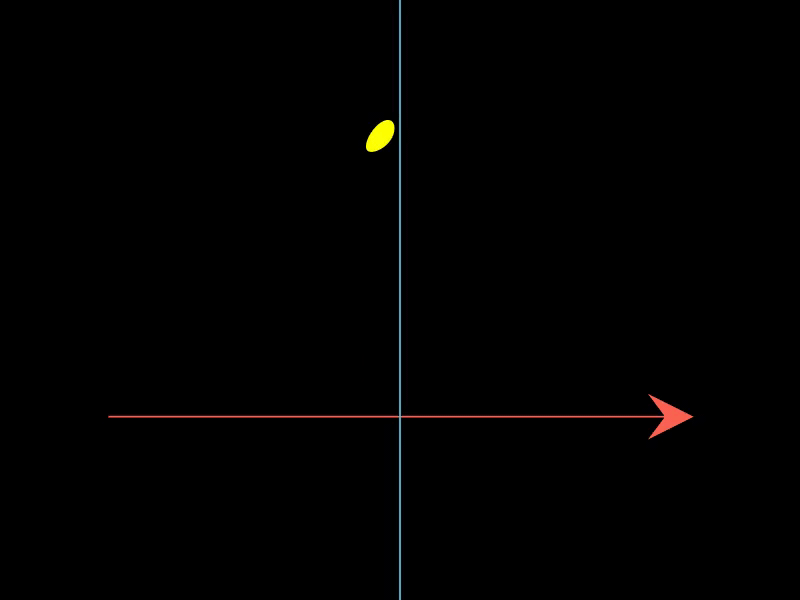
2.3. 展示简单谐振子的相空间轨迹
这个示例借助PhaseFlow展示了简单谐振子在相空间中的轨迹,根据谐振子的微分方程定义了向量场,动画展示了系统状态在相空间中的变化。
# 定义谐振子的微分方程
def harmonic_oscillator_deriv(state):
# x, v = state
dxdt = state[1]
dvdt = -1 * state[0]
return np.array([dxdt, dvdt, 0])
# 创建相空间中的点(初始位置)
initial_state = np.array([1.0, 0.0])
state_dot = Dot(point=axes.c2p(*initial_state), color=YELLOW)
self.add(state_dot)
# 使用PhaseFlow展示相空间轨迹
self.play(
PhaseFlow(
harmonic_oscillator_deriv,
state_dot,
virtual_time=5,
rate_func=linear,
),
run_time=5,
)
2.4. 模拟单摆运动在相空间轨迹
这个示例使用 PhaseFlow 根据单摆的微分方程来展示其在相空间中的轨迹,以此模拟单摆运动在相空间的动态行为。
# 定义单摆的微分方程
def pendulum_deriv(state):
theta, omega = state[:2]
g = 9.8 # 重力加速度
L = 1.0 # 单摆长度
dtheta_dt = omega
domega_dt = -g / L * np.sin(theta)
return np.array([dtheta_dt, domega_dt, 0])
# 创建相空间中的点(初始位置)
# 初始角度为 45 度,初始角速度为 0
initial_state = np.array([np.pi / 4, 0.0])
state_dot = Dot(point=axes.c2p(*initial_state), color=YELLOW)
self.add(state_dot)
# 使用 PhaseFlow 展示单摆相空间轨迹
self.play(
PhaseFlow(
pendulum_deriv,
state_dot,
virtual_time=5,
rate_func=linear,
),
run_time=5,
)
3. 附件
文中的代码只是关键部分的截取,完整的代码共享在网盘中(move.py),
下载地址: 完整代码 (访问密码: 6872)




