manim边做边学--多面体
在Manim中,对于多面体,有一系列封装好的类可以直接使用。
使用它们,可以方便快速的构建正多面体:
Polyhedron:通过顶点和面的参数构建任意多面体Tetrahedron:四面体Octahedron:八面体Dodecahedron:十二面体Icosahedron:二十面体
这些类使得在动画中直观地展示多面体成为可能,有助于理解多面体的几何形状和它们的属性。
特别是在数学和科学教学中,使用这些类制作的动画可以增强教学效果,使学生更容易理解抽象的几何概念。
1. 主要参数
Tetrahedron,Octahedron,Dodecahedron和Icosahedron都是正多面体,
所以参数比较简单,只有一个edge_length,表示多面体的边长。
Polyhedron作为不定面数的多面体,参数稍微多一些:
| 参数名称 | 类型 | 说明 |
|---|---|---|
| vertex_coords | [[float]] / np.ndarray | 定义多面体所有顶点的坐标 |
| faces_list | [[int]] | 定义多面体的各个面 |
| faces_config | dict | 为多面体的面提供额外的配置信息 |
| graph_config | dict | 配置多面体的图结构 |
参数faces_list中定义的是面的顶点索引(也就是参数vertex_coords中顶点的索引),可以确定多面体的各个面的形状和位置。
参数faces_config为多面体的面设置颜色、透明度、材质等属性,从而增强动画的视觉效果。
参数graph_config用于调整多面体图的连通性、边的权重等属性,这在某些特定的数学动画或物理模拟中可以发挥作用。
2. 主要方法
这些多面体的类没有什么自己特有的方法,通用的设置样式和动画(比如平移,旋转和缩放等)的方法都支持。
3. 使用示例
下面通过几个示例来演示各个多面体在动画中的应用。
3.1. 自定义多面体
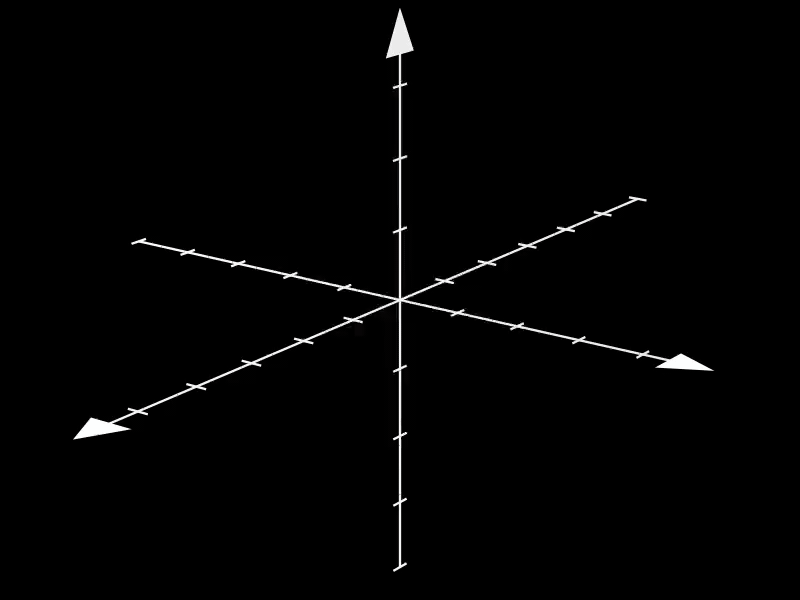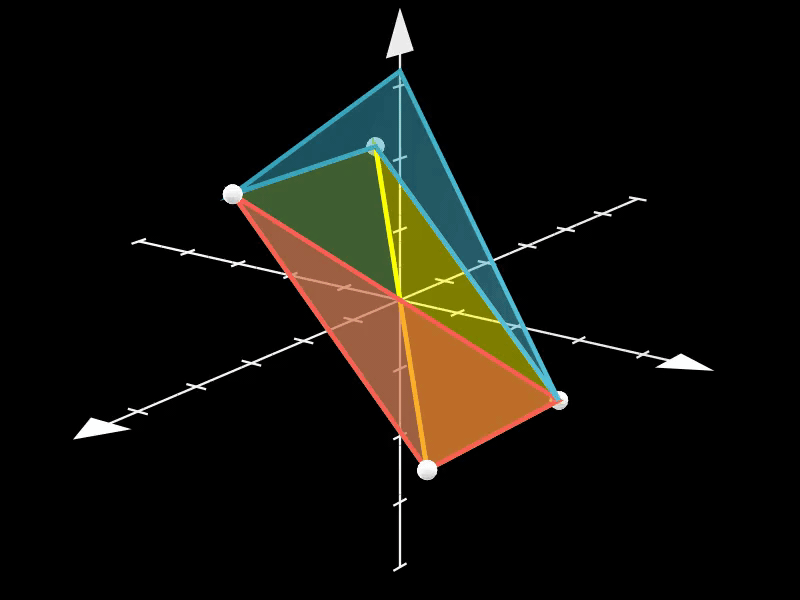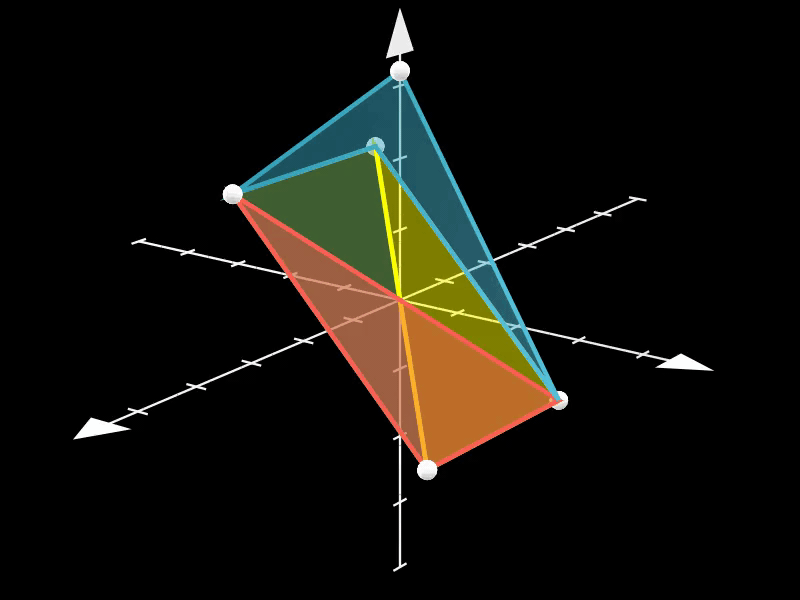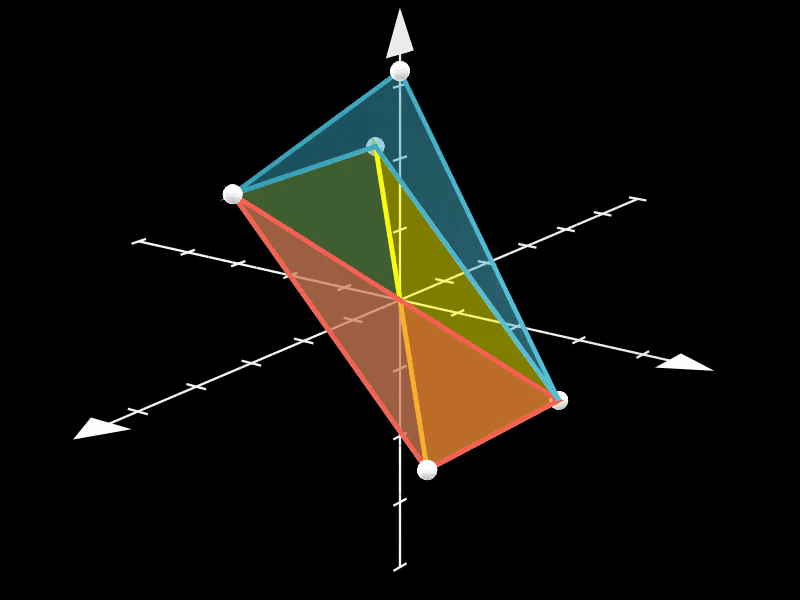
此示例展示了如何使用Polyhedron类创建自定义多面体。
通过定义顶点坐标和面列表,可以创建任意形状的多面体。
# 定义顶点坐标
vertex_coords = [
[1, 1, -1],
[1, -1, 1],
[-1, -1, 1],
[-1, 1, -1],
[0, 0, 2],
]
# 定义面(由顶点索引组成)
faces_list = [
[0, 1, 2],
[0, 2, 3],
[0, 3, 1],
[1, 2, 3, 4],
]
# 创建Polyhedron对象
p = Polyhedron(vertex_coords, faces_list)
p.faces[0].set_color(GREEN)
p.faces[1].set_color(YELLOW)
p.faces[2].set_color(RED)
p.faces[3].set_color(BLUE)
self.play(Create(p))
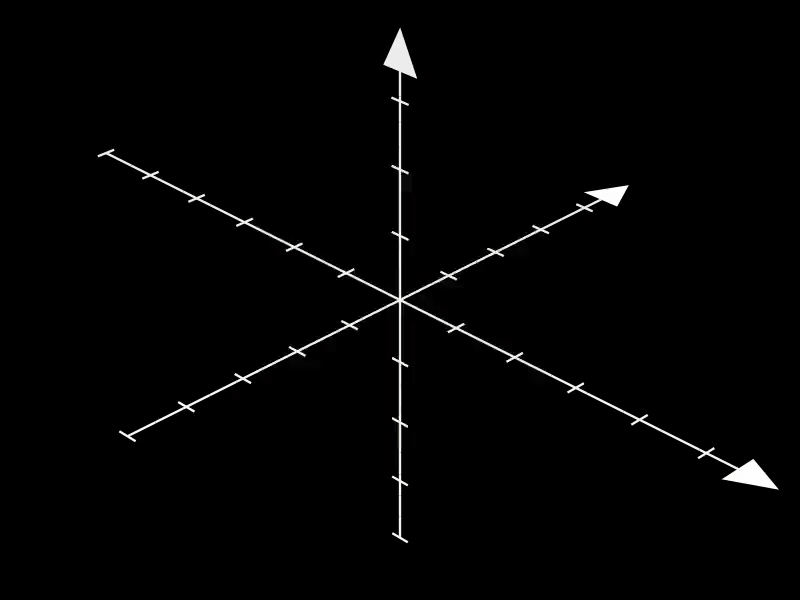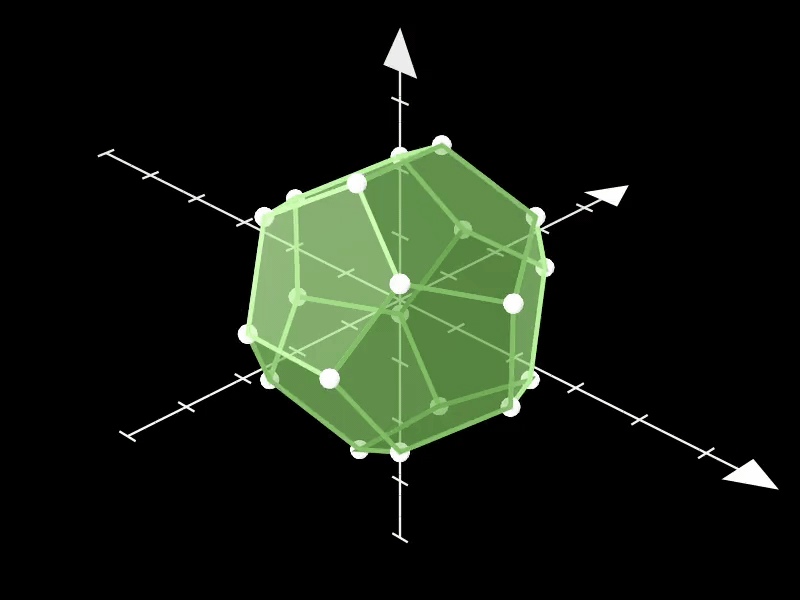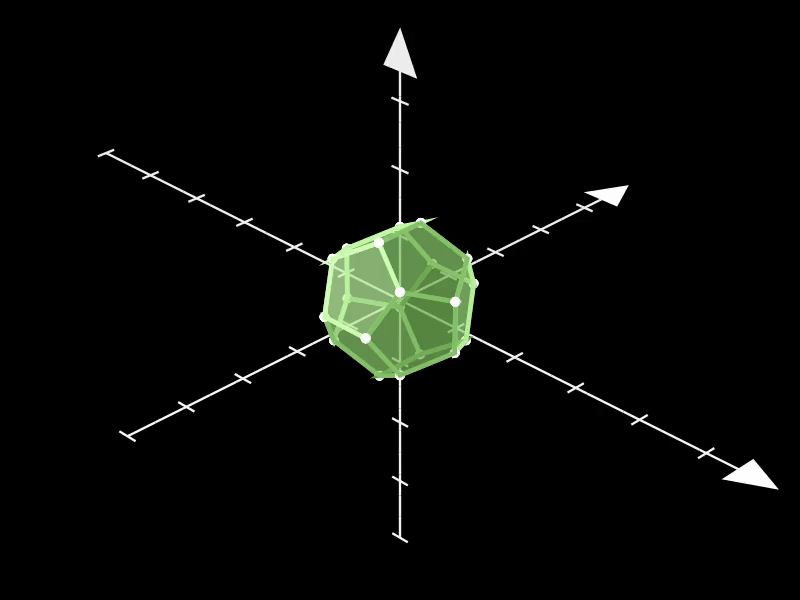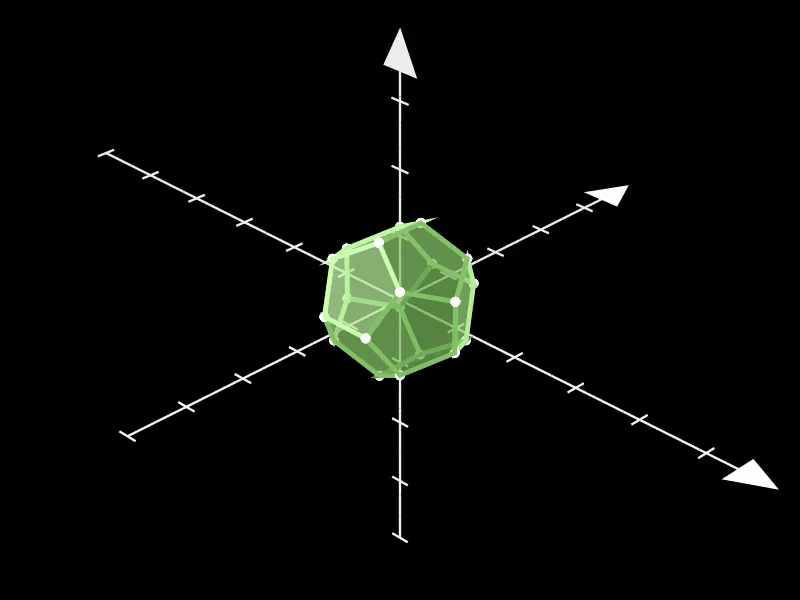
3.2. 十二面体
此示例展示了Dodecahedron类的使用,该类是Polyhedron的一个特例,用于创建标准的十二面体。
无需手动定义顶点和面,只需实例化对象并设置颜色等属性。
# 创建十二面体对象
d = Dodecahedron()
d.faces.set_color(GREEN)
self.play(Create(d))
self.play(d.animate.scale(0.5))
3.3. 二十面体
此示例展示了Icosahedron类的使用,该类用于创建标准的二十面体。
通过设置fill_opacity属性,可以控制多面体的填充透明度,
此外,通过旋转多面体,可以展示其不同的视角。
# 创建二十面体对象
i = Icosahedron()
i.faces.set_color(RED)
i.faces.set_opacity(0.6)
self.play(Create(i))
# 旋转多面体以展示其形状
self.play(i.animate.rotate(PI / 4, axis=OUT))
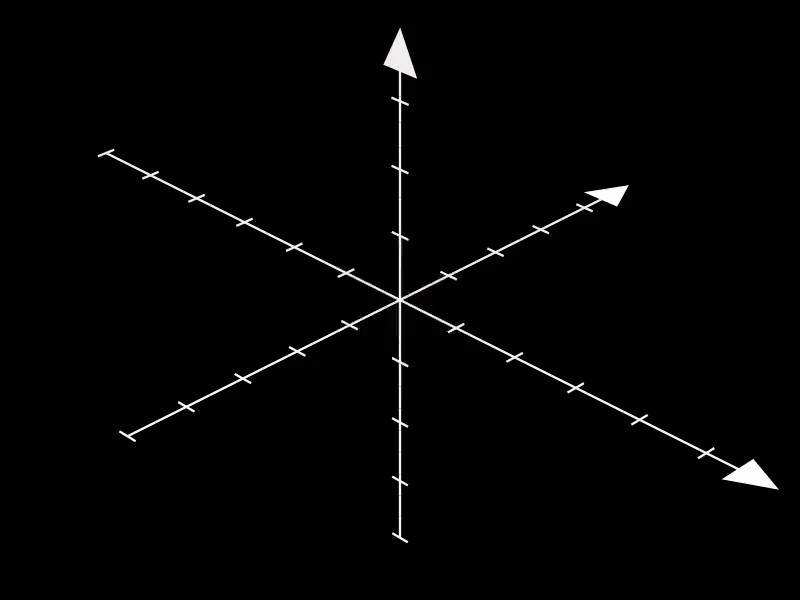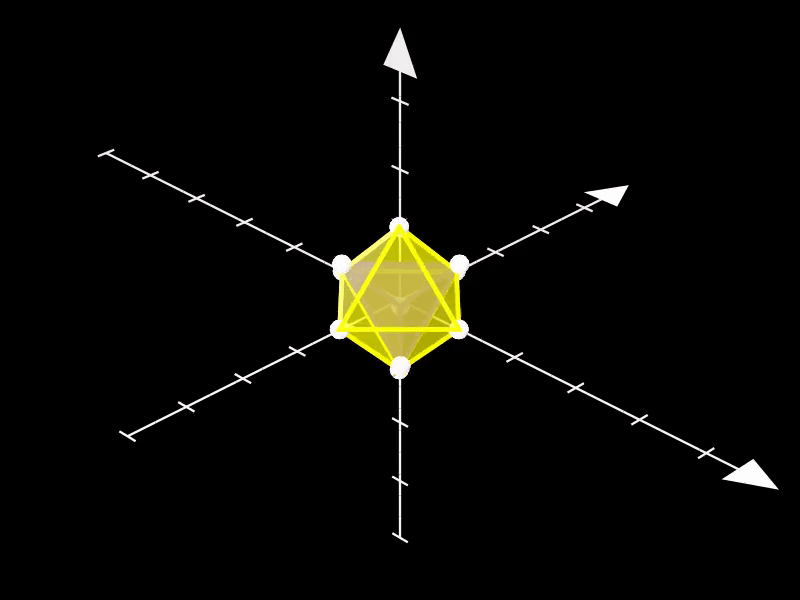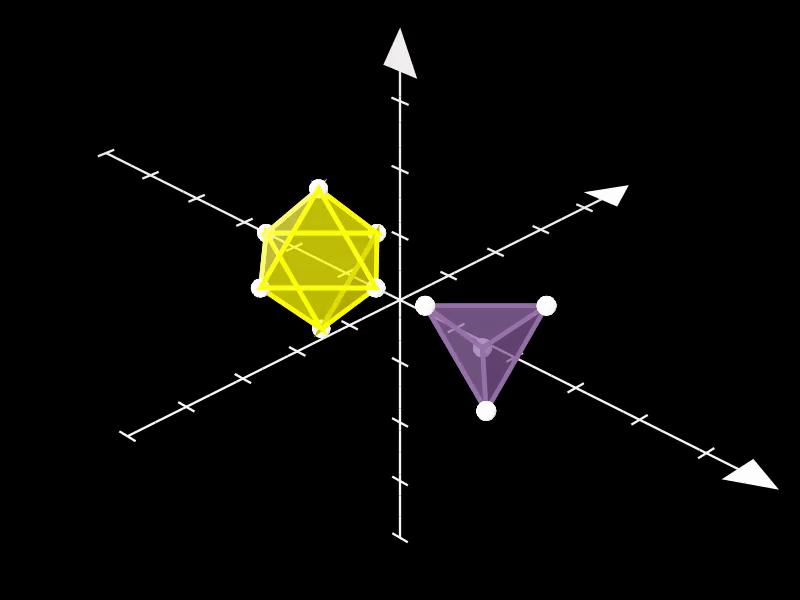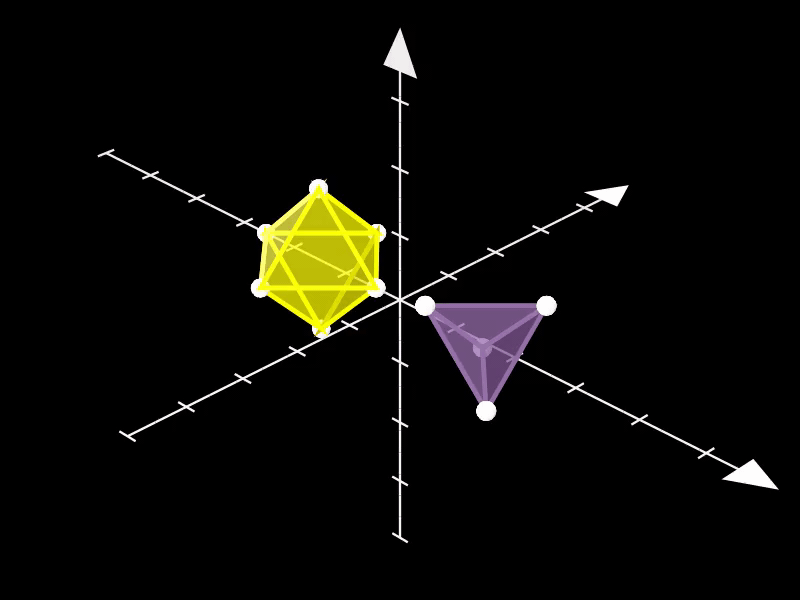
3.4. 八面体与四面体
此示例同时展示了Octahedron和Tetrahedron类的使用,这两个类分别用于创建标准的八面体和四面体。
通过将它们移动到场景的不同位置,可以清晰地展示这两个多面体的形状和大小差异。
# 创建八面体对象
o = Octahedron()
o.faces.set_color(YELLOW)
# 创建四面体对象
t = Tetrahedron()
t.faces.set_color(PURPLE)
self.play(Create(o), Create(t))
self.play(
o.animate.move_to(LEFT),
t.animate.move_to(RIGHT),
)
4. 附件
文中的代码只是关键部分的截取,完整的代码共享在网盘中(polyhedron.py),
下载地址: 完整代码 (访问密码: 6872)


