基尼系数的直观解释
我们在使用分类算法训练数据后,评价分类模型的优劣时,经常会遇到一个词,“基尼系数”。
那么,什么是基尼系数呢?
本文将尝试用最简单的方式介绍什么是“基尼系数”以及它的计算方法和意义。
希望能让大家对基尼系数有个直观的印象,而不仅仅是记住它枯燥的计算公式。
1. 从分类模型开始
首先,先假设有一个分类案例,包含2个种类的数据(紫色和蓝色),每个分类的数据有10个。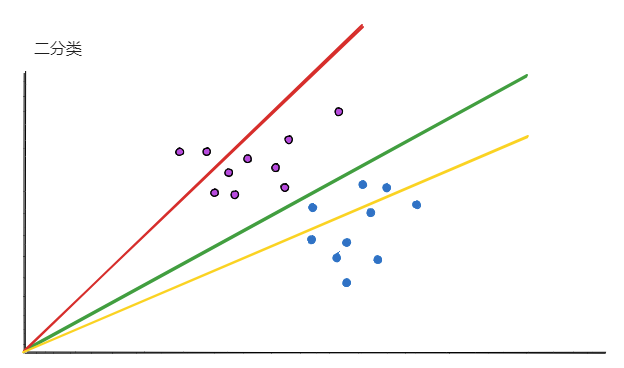
上图中的3种不同颜色的直线,代表3种不同参数的分类模型。
从图中可以看出:
- 绿色的线分类效果最好,完美分割了2个种类的数据
- 黄色次之,有3个蓝色的数据分类错误
- 红色的分类效果最差,有8个紫色的数据分类错误
对于上面这种简单的数据(只有2个维度的10个数据)和简单的分类模型(线性分类)来说,
我们通过作图可以一眼看出哪个分类模型的效果最好。
而现实中的实际情况,往往是不仅数据量大,数据维度也很多,分类模型也不会仅仅是一条二维直线。
这时,无法像上面那样绘制出二维图形来,那么该如何去定量的评估一个分类模型的好坏呢?
2. 基尼系数
基尼系数就是这样一种指标,通过一个分类模型的基尼系数(Gini),来帮助我们判断分类模型的好坏。
2.1. 绿色模型
对于绿色的分类模型: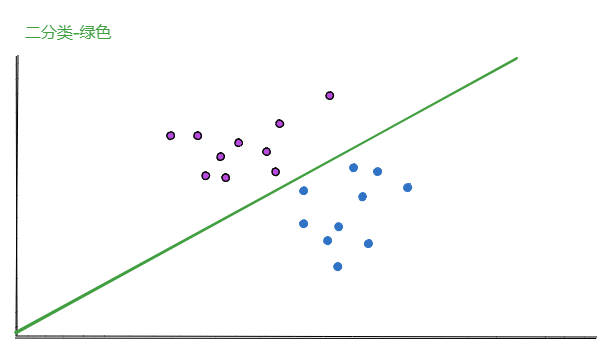
| 分类过程 | 分类结果 | 概率 |
|---|---|---|
| 选择 紫色 数据,并且被分类为 紫色 | 正确 | 50% |
| 选择 紫色 数据,并且被分类为 蓝色 | 错误 | 0% |
| 选择 蓝色 数据,并且被分类为 蓝色 | 正确 | 50% |
| 选择 蓝色 数据,并且被分类为 紫色 | 错误 | 0% |
概率计算方式说明:比如对于表格第一行,【选择 紫色 数据,并且被分类为 紫色】的概率。
首先,【选择 紫色 数据】的概率为50%,因为总共20条数据,紫色数据有10条。
其次,【并且被分类为** 紫色**】的概率为100%,因为绿色的模型可以正确分类所有的数据。
所以,【选择 紫色 数据,并且被分类为 紫色】的概率为 50% x 100% = 50%。
其余3行的概率同上一样计算。
2.2. 黄色模型
对于黄色的模型: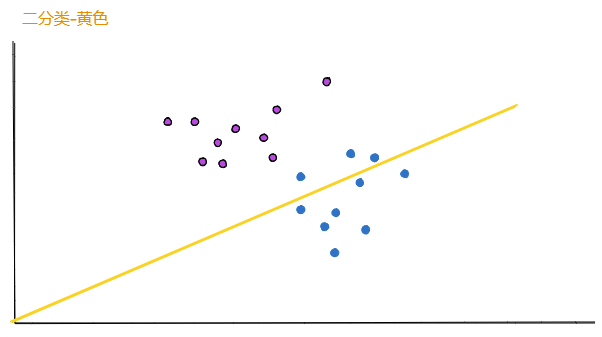
| 分类过程 | 分类结果 | 概率 |
|---|---|---|
| 选择 紫色 数据,并且被分类为 紫色 | 正确 | 50% |
| 选择 紫色 数据,并且被分类为 蓝色 | 错误 | 0% |
| 选择 蓝色 数据,并且被分类为 蓝色 | 正确 | 35% |
| 选择 蓝色 数据,并且被分类为 紫色 | 错误 | 15% |
对于上面表格中的第三行,【选择 蓝色 数据,并且被分类为 蓝色】为什么是35%?
首先,【选择 蓝色 数据】的概率为50%,因为总共20条数据,蓝色数据有10条。
其次,【并且被分类为 蓝色】的概率是70%,从图中可以看出黄色的模型对于10条蓝色数据,有7条分类正确,有3条被错误分类到紫色的那一类中了。
所以,【选择 蓝色 数据,并且被分类为 蓝色】的概率为 50% x 70% = 35%。
表格第四行的15%也是同样方式计算出的。
2.3. 红色模型
最后,看下红色的模型: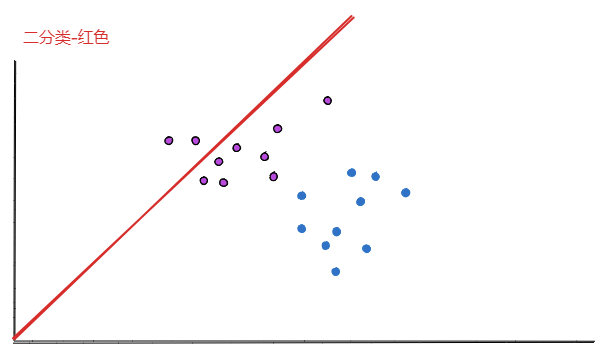
| 分类过程 | 分类结果 | 概率 |
|---|---|---|
| 选择 紫色 数据,并且被分类为 紫色 | 正确 | 10% |
| 选择 紫色 数据,并且被分类为 蓝色 | 错误 | 40% |
| 选择 蓝色 数据,并且被分类为 蓝色 | 正确 | 50% |
| 选择 蓝色 数据,并且被分类为 紫色 | 错误 | 0% |
计算方式前面已经介绍,这里不再赘述。
2.4. 计算公式
3种不同效果的分类模型的分类效果统计在上面的表格中。
根据这些概率,我们如何给模型打分,从而确定模型好坏呢?
答案就是基尼系数(Gini),这时我们再来看看基尼系数的计算公式:
\(Gini = \sum_{i=1}^C p(i)\times (1-p(i))\)
其中,\(C\)是数据的总类别数量,本文的例子中有两类数据,所以 \(C=2\)
\(p(i)\)是选择某个类别\(i\)的数据的概率。
下面来看看本文中的3个模型的基尼系数分别是多少。
我们假设 \(p(1)\)代表选中紫色数据的概率;\(p(2)\)代表选中蓝色数据的概率
那么,对于绿色模型,
绿色线上部分的基尼系数:\(G_{up} = p(1)\times(1-p(1)) + p(2)(1-p(2))\)
在绿色线上部分,全是紫色数据,所以 \(p(1) = 1,\quad p(2)=0\);
因此,\(G_{up} = 1\times(1-1)+0\times(1-0) = 0\)
对于绿色线下部分,同理可计算出\(G_{down}=0\)
又因为绿色线上下部分的数据量都是10条,各占总数据量的50%,
所以最终绿色模型整体的基尼系数:\(G_{green}=50\% G_{up} + 50\% G_{down} = 0\)
对于黄色模型:
在黄色线上部分,10个紫色数据,3个蓝色数据,所以 \(p(1) = \frac{10}{13},\quad p(2)=\frac{3}{13}\),
因此,\(G_{up} = \frac{10}{13}\times(1-\frac{10}{13})+\frac{3}{13}\times(1-\frac{3}{13}) \approx 0.355\)
黄色线下部分,0个紫色数据,7个蓝色数据,所以 \(p(1) = 0,\quad p(2)=1\),所以\(G_{down}=0\)
又因为黄色线上下部分的数据量分别13条和7条,各占总数据量的\(\frac{13}{20},\quad \frac{7}{20}\),
所以最终黄色模型整体的基尼系数:\(G_{yellow}=\frac{13}{20} G_{up} + \frac{7}{20} G_{down} \approx 0.23\)
对于红色模型:
和上面同理计算出:\(G_{up}=0\),\(G_{down} \approx 0.494\);
\(G_{red} = \frac{2}{20} \times G_{up} + \frac{18}{20}\times G_{down} \approx 0.444\)
基尼系数是介于0~1的数值,且越小表示效果越好,
因为 \(G_{green}=0<G_{yellow}=0.23<G_{red}=0.444\)
所以 绿色模型 优于 黄色模型 优于 红色模型。
3. 总结
通过比较不同模型的基尼系数的值,不仅可以一下看出分类模型的好坏,还可以根据数值的大小了解究竟好多少。
基尼系数也为我们训练分类模型时提供了一个优化的方向,
一方面,对于不同的分类模型,我们可以通过比较它们的基尼系数,确定哪种模型效果更好;
另一方面,对于同一个分类模型,我们可以通过观察其中每个分类的基尼系数(比如上面的\(G_{up}\)和\(G_{down}\)),
从而确定那个分类的效果比较差,那就是重点优化的方向。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号