【matplotlib 实战】--散点图
散点图,又名点图、散布图、X-Y图,是将所有的数据以点的形式展现在平面直角坐标系上的统计图表。
散点图常被用于分析变量之间的相关性。
如果两个变量的散点看上去都在一条直线附近波动,则称变量之间是线性相关的;
如果所有点看上去都在某条曲线(非直线)附近波动,则称此相关为非线形相关的;
如果所有点在图中没有显示任何关系,则称变量间是不相关的。
散点图一般需要两个不同变量,一个沿x轴绘制,另一个沿y轴绘制。
众多的散点叠加后,有助于展示数据集的“整体景观”,从而帮助我们分析两个变量之间的相关性,或找出趋势和规律。
1. 主要元素
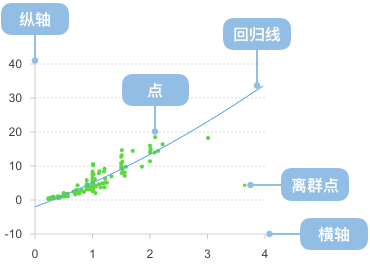
散点图的主要元素包括:
- 横轴:表示自变量。
- 纵轴:表示因变量。
- 数据点:每个数据点代表一个观测值,它在坐标轴上的位置表示两个变量的对应取值。
- 趋势线:趋势线是通过数据点拟合出的一条线,用于显示变量之间的趋势或关联性。
2. 适用的场景
散点图适用的分析场景包括:
- 变量关系探索:帮助我们观察和理解两个变量之间的关系。通过观察数据点的分布情况和趋势线的形状,可以判断变量之间是否存在线性关系、非线性关系或无关系。
- 趋势分析:用于分析趋势和预测。通过观察趋势线的方向和斜率进行预测。
- 群体分析:散点图可以帮助我们观察和识别数据点的聚类情况。
- 异常值检测:散点图可以用于检测异常值或离群点。
3. 不适用的场景
散点图不适用的分析场景包括:
- 时间序列分析:散点图主要用于展示两个变量之间的关系,对于时间序列数据,通常使用折线图或其他适合展示时间变化的图表类型。
- 多变量分析:散点图只能展示两个变量之间的关系,对于多个变量之间的关系分析,需要使用其他图表类型,如散点矩阵、平行坐标图等。
- 分布分析:散点图主要关注变量之间的关系,而不是变量本身的分布情况。如果需要分析变量的分布特征,可以使用直方图、箱线图等图表类型。
4. 分析实战
散点图适合寻找两个变量之间的关系,本次分析 **空气污染 **方面的数据情况。
4.1. 数据来源
数据来源国家统计局公开的数据。
用到的两个统计数据分别是:
- 工业污染治理中,每年治理废气的投资额
- 废气中二氧化硫的每年排放量情况
整理好的数据可从下面的地址下载:
https://databook.top/nation/A0CA0C05.csv(废气中主要污染物排放) 和 A0C0I.csv(工业污染治理投资) 两个文件。
fp = "d:/share/data/A0C05.csv"
df1 = pd.read_csv(fp)
df1
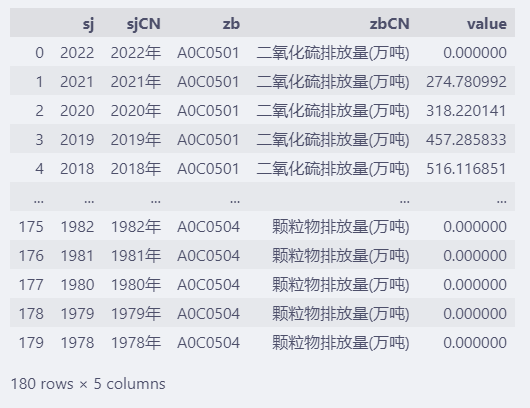
fp = "d:/share/data/A0C0I.csv"
df2 = pd.read_csv(fp)
df2
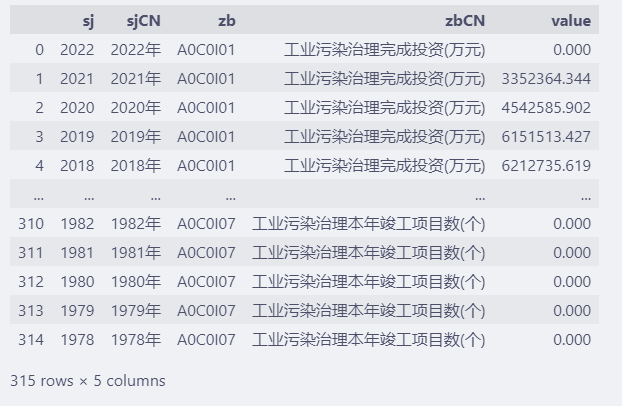
4.2. 数据清理
2022年数据是空的,所以从两个文件中分别提取 2012~2021年期间,汇总所有废气排放量(万吨)和**治理废气项目完成投资(万元) **两类数据绘制图形。
#所有废气的排放量
data_x = df1[(df1["sj"] >= 2012) &
(df1["sj"] <= 2021)]
data_x = data_x.loc[:, ["sj", "value"]]
data_x = data_x.groupby("sj").sum("value")
#治理废气项目投资 A0C0I03是治理废气投资的编号
data_y = df2[(df2["sj"] >= 2012) &
(df2["sj"] <= 2021) &
(df2["zb"] == "A0C0I03")]
data_y = data_y.sort_index(ascending=False)
4.3. 分析结果可视化
with plt.style.context("seaborn-v0_8"):
fig = plt.figure()
ax = fig.add_axes([0.1, 0.1, 0.6, 0.6])
ax.scatter(data_x["value"], data_y["value"]/10000)
ax.set_xlabel("废气排放量(万吨)")
ax.set_ylabel("治理废气项目完成投资(亿元)")
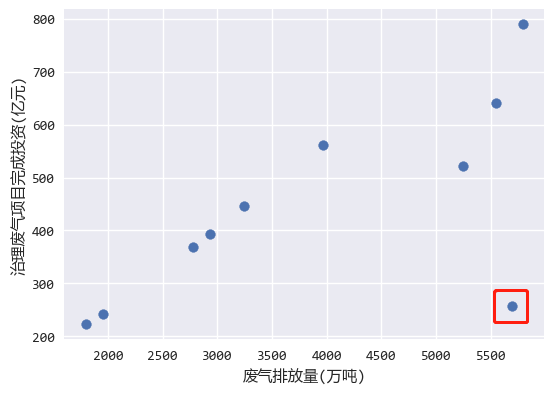
从分析结果图中来看,排放的废气量越大的时候,治理的投资费用也越高。
但是右下角红色框内有一个异常值,那个是2012年的数据。
估计那时候还不太重视环保,所以即使那时候废气排放量大,用于治理废气的投资费用也不高。



