BZOJ2816: [ZJOI2012]网络

题解:建c颗LCT 然后维护每一种颜色的LCT即可

#include <bits/stdc++.h>
const int MAXN=1e4+10;
using namespace std;
int ch[11][MAXN][2],pre[11][MAXN],key[11][MAXN],maxx[11][MAXN],res[11][MAXN],size[11][MAXN];
int du[11][MAXN];bool rt[11][MAXN];
int a[MAXN];
int n,m,c,k;
void reverse(int id,int r){
	if(!r)return ;
	swap(ch[id][r][0],ch[id][r][1]);
	res[id][r]^=1;
}
void push(int id,int r){
	if(res[id][r]){
		reverse(id,ch[id][r][0]);
		reverse(id,ch[id][r][1]);
		res[id][r]^=1;
	}
}
void up(int id,int r){
	maxx[id][r]=max(key[id][r],max(maxx[id][ch[id][r][0]],maxx[id][ch[id][r][1]]));
	size[id][r]=size[id][ch[id][r][0]]+size[id][ch[id][r][1]]+1;
}
void P(int id,int x){
	if(!rt[id][x])P(id,pre[id][x]);
	push(id,x);
}
void rotate(int id,int x,int kind){
	int y=pre[id][x];
	pre[id][ch[id][x][kind]]=y;ch[id][y][!kind]=ch[id][x][kind];
	if(rt[id][y])rt[id][y]=0,rt[id][x]=1;
	else ch[id][pre[id][y]][ch[id][pre[id][y]][1]==y]=x;
	pre[id][x]=pre[id][y];ch[id][x][kind]=y;pre[id][y]=x;
	up(id,y);
}
void splay(int id,int x){
	P(id,x);
	//cout<<"qkonb"<<endl;
	while(!rt[id][x]){
		if(rt[id][pre[id][x]])rotate(id,x,ch[id][pre[id][x]][0]==x);
		else{
			int y=pre[id][x];int kind=ch[id][pre[id][y]][0]==y;
			if(ch[id][y][kind]==x)rotate(id,x,!kind),rotate(id,x,kind);
			else rotate(id,y,kind),rotate(id,x,kind);
		}
	}
	up(id,x);
}
void access(int id,int x){
	int y=0;
	while(x){
		//cout<<id<<" "<<x<<endl;
		splay(id,x);
		//cout<<"qkpnb"<<endl;
		if(ch[id][x][1])rt[id][ch[id][x][1]]=1,pre[id][ch[id][x][1]]=x;
		if(y)rt[id][y]=0;
		ch[id][x][1]=y;up(id,x);
		y=x;x=pre[id][x];
	}
}
void mroot(int id,int x){
	access(id,x);
	splay(id,x);reverse(id,x);
}
bool querty(int id,int u,int v){
	while(pre[id][u])u=pre[id][u];
	while(pre[id][v])v=pre[id][v];
	return u==v;
}
bool pd(int id,int u,int v){
	mroot(id,u);access(id,v);splay(id,v);
	if(size[id][v]==2)return true;
	else return false;
}
void destory(int id,int u,int v){
	mroot(id,u);access(id,v);splay(id,v);
	ch[id][v][0]=ch[id][v][1]=0;up(id,v);
	pre[id][u]=0;rt[id][u]=1;up(id,u);
}
void Link(int id,int u,int v){
	mroot(id,u);pre[id][u]=v;
}
void update(int id,int v,int vul){
	splay(id,v);key[id][v]=vul;up(id,v);
}
int Maxx(int id,int u,int v){
	mroot(id,u);access(id,v);splay(id,v);
	return maxx[id][v];
}
void newnode(int id,int v,int vul){
	ch[id][v][0]=ch[id][v][1]=0;rt[id][v]=1;size[id][v]=1;key[id][v]=maxx[id][v]=vul;
	pre[id][v]=0;res[id][v]=0;du[id][v]=0;
}
int main(){
	scanf("%d%d%d%d",&n,&m,&c,&k);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	for(int i=0;i<c;i++){
		for(int j=1;j<=n;j++)newnode(i,j,a[j]);
	}
	int u,v,w;
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&u,&v,&w);
		du[w][u]++;du[w][v]++;Link(w,u,v);
	}
	int op,x,y,id;
	for(int i=1;i<=k;i++){
		scanf("%d",&op);
		if(op==0){
			scanf("%d%d",&x,&y);
			for(int j=0;j<c;j++)update(j,x,y);
		}
		else if(op==1){
			scanf("%d%d%d",&u,&v,&w);id=-1;
			for(int j=0;j<c;j++)if(querty(j,u,v)){
				if(pd(j,u,v)){id=j;break;}
			}
			if(id==-1){puts("No such edge.");continue;}
			du[id][u]--;du[id][v]--;destory(id,u,v);
			if(du[w][u]==2||du[w][v]==2){puts("Error 1.");Link(id,u,v);du[id][u]++;du[id][v]++;continue;}
			if(querty(w,u,v)){puts("Error 2.");Link(id,u,v);du[id][u]++;du[id][v]++;continue;}
			Link(w,u,v);du[w][u]++;du[w][v]++;
			puts("Success.");
		}
		else {
			scanf("%d%d%d",&w,&u,&v);
			if(!querty(w,u,v))puts("-1");
			else printf("%d\n",Maxx(w,u,v));
		}
	}
	return 0;
}

 

题目描述

有一个无向图G，每个点有个权值，每条边有一个颜色。这个无向图满足以下两个条件：

  1. 对于任意节点连出去的边中，相同颜色的边不超过两条。

  2. 图中不存在同色的环，同色的环指相同颜色的边构成的环。

在这个图上，你要支持以下三种操作：

  1. 修改一个节点的权值。

  2. 修改一条边的颜色。

  3. 查询由颜色c的边构成的图中，所有可能在节点u到节点v之间的简单路径上的节点的权值的最大值。

输入输出格式

输入格式：

输入文件network.in的第一行包含四个正整数N, M, C, K，其中N为节点个数，M为边数，C为边的颜色数，K为操作数。

接下来N行，每行一个正整数vi，为节点i的权值。

之后M行，每行三个正整数u, v, w，为一条连接节点u和节点v的边，颜色为w。满足1 ≤ u, v ≤ N，0 ≤ w < C，保证u ≠ v，且任意两个节点之间最多存在一条边(无论颜色)。

最后K行，每行表示一个操作。每行的第一个整数k表示操作类型。

  1. k = 0为修改节点权值操作，之后两个正整数x和y，表示将节点x的权值vx修改为y。

  2. k = 1为修改边的颜色操作，之后三个正整数u, v和w，表示将连接节点u和节点v的边的颜色修改为颜色w。满足0 ≤ w < C。

  3. k = 2为查询操作，之后三个正整数c, u和v，表示查询所有可能在节点u到节点v之间的由颜色c构成的简单路径上的节点的权值的最大值。如果不存在u和v之间不存在由颜色c构成的路径，那么输出“-1”。

输出格式：

输出文件network.out包含若干行，每行输出一个对应的信息。

  1. 对于修改节点权值操作，不需要输出信息。

  2. 对于修改边的颜色操作，按以下几类输出：

a) 若不存在连接节点u和节点v的边，输出“No such edge.”。

b) 若修改后不满足条件1，不修改边的颜色，并输出“Error 1.”。

c) 若修改后不满足条件2，不修改边的颜色，并输出“Error 2.”。

d) 其他情况，成功修改边的颜色，并输出“Success.”。

输出满足条件的第一条信息即可，即若同时满足b和c，则只需要输出“Error 1.”。

  1. 对于查询操作，直接输出一个整数。

输入输出样例

输入样例#1： 复制 
4 5 2 7
1
2
3
4
1 2 0
1 3 1
2 3 0
2 4 1
3 4 0
2 0 1 4
1 1 2 1
1 4 3 1
2 0 1 4
1 2 3 1
0 2 5
2 1 1 4
输出样例#1： 复制 
4
Success.
Error 2.
-1
Error 1.
5

说明

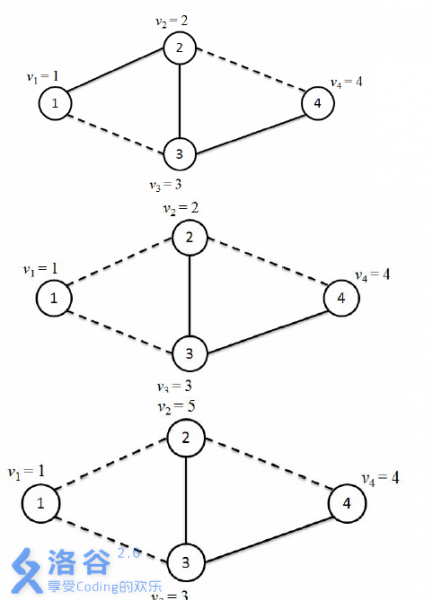
颜色0为实线的边，颜色1为虚线的边，

由颜色0构成的从节点1到节点4的路径有1 – 2 – 4，故max{v1, v2, v4} = max{ 1, 2, 4 } = 4。

将连接节点1和节点2的边修改为颜色1，修改成功，输出“Success.”

将连接节点4和节点3的边修改为颜色1，由于修改后会使得存在由颜色1构成的环( 1 – 2 – 4 – 3 – 1 )，不满足条件2，故不修改，并输出“Error 2”。

不存在颜色0构成的从节点1到节点4的边，输出“-1”。

将连接节点2和节点3的边修改为颜色1，由于修改后节点2的连出去的颜色为1的边有3条，故不满足条件1，故不修改，并输出“Error 1.”。

将节点2的权值修改为5。

由颜色1构成的从节点1到节点4的路径有 1 – 2 – 4，故max{v1, v2, v4} = max{ 1, 5, 4 } = 5。

【数据规模】

对于30%的数据：N ≤ 1000，M ≤ 10000，C ≤ 10，K ≤ 1000。

另有20%的数据：N ≤ 10000，M ≤ 100000，C = 1，K ≤ 100000。

对于100%的数据：N ≤ 10000，M ≤ 100000，C ≤ 10，K ≤ 100000。

posted @ 2018-08-14 15:05  wang9897  阅读(110)  评论(0)  编辑  收藏  举报