Educational Codeforces Round 37 (Rated for Div. 2)

(:原题上分场 但是.....数论+线段树写挂了！！写挂了！！！ 总觉得是原题 然后没有仔细思考  ...数论都推完了  线段树想当然...这次上分就靠了这个板子题....23333哪里每次都有这么好的运气 所以赛后及时补题 学到了很多

　　　　　　　　　　　　　　　　　　A. Water The Garden

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

It is winter now, and Max decided it's about time he watered the garden.

The garden can be represented as n consecutive garden beds, numbered from 1 to n. k beds contain water taps (i-th tap is located in the bed x_i), which, if turned on, start delivering water to neighbouring beds. If the tap on the bed x_i is turned on, then after one second has passed, the bed x_i will be watered; after two seconds have passed, the beds from the segment [x_i - 1, x_i + 1] will be watered (if they exist); after j seconds have passed (j is an integer number), the beds from the segment [x_i - (j - 1), x_i + (j - 1)] will be watered (if they exist). Nothing changes during the seconds, so, for example, we can't say that the segment [x_i - 2.5, x_i + 2.5] will be watered after 2.5 seconds have passed; only the segment [x_i - 2, x_i + 2] will be watered at that moment.

The garden from test 1. White colour denotes a garden bed without a tap, red colour — a garden bed with a tap. The garden from test 1 after 2 seconds have passed after turning on the tap. White colour denotes an unwatered garden bed, blue colour — a watered bed.

Max wants to turn on all the water taps at the same moment, and now he wonders, what is the minimum number of seconds that have to pass after he turns on some taps until the whole garden is watered. Help him to find the answer!

Input

The first line contains one integer t — the number of test cases to solve (1 ≤ t ≤ 200).

Then t test cases follow. The first line of each test case contains two integers n and k (1 ≤ n ≤ 200, 1 ≤ k ≤ n) — the number of garden beds and water taps, respectively.

Next line contains k integers x_i (1 ≤ x_i ≤ n) — the location of i-th water tap. It is guaranteed that for each 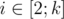condition x_i - 1 < x_i holds.

It is guaranteed that the sum of n over all test cases doesn't exceed 200.

Note that in hacks you have to set t = 1.

Output

For each test case print one integer — the minimum number of seconds that have to pass after Max turns on some of the water taps, until the whole garden is watered.

Example

Input

3
5 1
3
3 3
1 2 3
4 1
1

Output

3
1
4

A题纯暴力 维护两个喷泉的距离/2(细节处理是否加1 和两端的最大值

#include <bits/stdc++.h>
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f*x;
}
int a[205];
int main(){
	ios::sync_with_stdio(false);
	int n,k;int T;cin>>T;
	while(T--){
		cin>>n>>k;
		for(int i=1;i<=k;i++) cin>>a[i];
		int maxn=a[1]-1;int t1;
		for(int i=2;i<=k;i++){
			int t=a[i]-a[i-1]-1;
			if(t%2==0) t1=t/2;
			else t1=t/2+1;
			maxn=max(maxn,t1);
		}
		maxn=max(n-a[k],maxn)+1;
		cout<<maxn<<endl;
	}
	return 0;
}

 

　　　　　　　　　　　　　　B. Tea Queue

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Recently n students from city S moved to city P to attend a programming camp.

They moved there by train. In the evening, all students in the train decided that they want to drink some tea. Of course, no two people can use the same teapot simultaneously, so the students had to form a queue to get their tea.

i-th student comes to the end of the queue at the beginning of l_i-th second. If there are multiple students coming to the queue in the same moment, then the student with greater index comes after the student with lesser index. Students in the queue behave as follows: if there is nobody in the queue before the student, then he uses the teapot for exactly one second and leaves the queue with his tea; otherwise the student waits for the people before him to get their tea. If at the beginning of r_i-th second student i still cannot get his tea (there is someone before him in the queue), then he leaves the queue without getting any tea.

For each student determine the second he will use the teapot and get his tea (if he actually gets it).

Input

The first line contains one integer t — the number of test cases to solve (1 ≤ t ≤ 1000).

Then t test cases follow. The first line of each test case contains one integer n (1 ≤ n ≤ 1000) — the number of students.

Then n lines follow. Each line contains two integer l_i, r_i (1 ≤ l_i ≤ r_i ≤ 5000) — the second i-th student comes to the end of the queue, and the second he leaves the queue if he still cannot get his tea.

It is guaranteed that for every 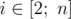condition l_i - 1 ≤ l_i holds.

The sum of n over all test cases doesn't exceed 1000.

Note that in hacks you have to set t = 1.

Output

For each test case print n integers. i-th of them must be equal to the second when i-th student gets his tea, or 0 if he leaves without tea.

Example

Input

2
2
1 3
1 4
3
1 5
1 1
2 3

Output

1 2 
1 0 2 
B题 排队递水...写一个sort 按照起始从小到大 起始相同标号从小到大的顺序排序 然后一边扫即可

#include <bits/stdc++.h>
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f*x;
}
typedef struct node{
	int l,r,biao;
	friend bool operator <(node aa,node bb){
		if(aa.l==bb.l) return aa.biao<bb.biao;
		return aa.l<bb.l;
	}
}node;
node d[1005];
int ans[1005];
int main(){
	ios::sync_with_stdio(false);
	int n;int T;cin>>T;
	while(T--){
		cin>>n;
		for(int i=1;i<=n;i++){
			cin>>d[i].l>>d[i].r;
			d[i].biao=i;
		}
		sort(d+1,d+n+1);
		int t=1;
		memset(ans,0,sizeof(ans));
		for(int i=1;i<=n;i++){
			if(d[i].l>t) t=d[i].l;
			else if(d[i].r<t) continue;
			ans[d[i].biao]=t;
			t++;
		}
		for(int i=1;i<=n;i++){
			if(i==1) cout<<ans[i];
			else cout<<" "<<ans[i];
		}
		cout<<endl;
	}
	return 0;
}

 

　　　　　　　　　　　　　　　　　　C　. Swap Adjacent Elements

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You have an array a consisting of n integers. Each integer from 1 to n appears exactly once in this array.

For some indices i (1 ≤ i ≤ n - 1) it is possible to swap i-th element with (i + 1)-th, for other indices it is not possible. You may perform any number of swapping operations any order. There is no limit on the number of times you swap i-th element with (i + 1)-th (if the position is not forbidden).

Can you make this array sorted in ascending order performing some sequence of swapping operations?

Input

The first line contains one integer n (2 ≤ n ≤ 200000) — the number of elements in the array.

The second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 200000) — the elements of the array. Each integer from 1 to n appears exactly once.

The third line contains a string of n - 1 characters, each character is either 0 or 1. If i-th character is 1, then you can swap i-th element with (i + 1)-th any number of times, otherwise it is forbidden to swap i-th element with (i + 1)-th.

Output

If it is possible to sort the array in ascending order using any sequence of swaps you are allowed to make, print YES. Otherwise, print NO.

Examples

Input

6
1 2 5 3 4 6
01110

Output

YES

Input

6
1 2 5 3 4 6
01010

Output

NO

C题  交了一发并查集(跑的贼快23333 按照01 如果是1 则相邻位置合并 然后一边扫过去 如果当前a[i]与此时的i 在一个集合内则是合法的  判断整个过程是否出现不合法的情况

#include <bits/stdc++.h>
#define N 200005
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f*x;
}
int a[N];
int fa[N];
int find(int x){
	if(x!=fa[x]) return fa[x]=find(fa[x]);
	return x;
}
int main(){
	ios::sync_with_stdio(false);
	int n;scanf("%d",&n);
	for(int i=1;i<=n;i++) {
	scanf("%d",&a[i]);fa[i]=i;  
}
	char ch;
	for(int i=1;i<n;i++){
		scanf(" %c",&ch);
		//cout<<t<<endl;
		if(ch=='1') fa[i+1]=fa[i];
	}
	for(int i=1;i<=n;i++){
		int t1=find(a[i]);int t2=find(i);
		if(t1!=t2){
			cout<<"NO"<<endl;
			return 0;
		}
	}
	cout<<"YES"<<endl;
	return 0;
}

 D题   看题解说是DP+数论   非DP&&非数学选手 选择性跳过

 E题  求补图的联通块的大小和数目

 

　　　　　　　　　　　　E. Connected Components?

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an undirected graph consisting of n vertices and 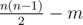edges. Instead of giving you the edges that exist in the graph, we give you m unordered pairs (x, y) such that there is no edge between x and y, and if some pair of vertices is not listed in the input, then there is an edge between these vertices.

You have to find the number of connected components in the graph and the size of each component. A connected component is a set of vertices X such that for every two vertices from this set there exists at least one path in the graph connecting these vertices, but adding any other vertex to X violates this rule.

Input

The first line contains two integers n and m (1 ≤ n ≤ 200000, ).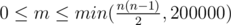

Then m lines follow, each containing a pair of integers x and y (1 ≤ x, y ≤ n, x ≠ y) denoting that there is no edge between x and y. Each pair is listed at most once; (x, y) and (y, x) are considered the same (so they are never listed in the same test). If some pair of vertices is not listed in the input, then there exists an edge between those vertices.

Output

Firstly print k — the number of connected components in this graph.

Then print k integers — the sizes of components. You should output these integers in non-descending order.

Example

Input

5 5
1 2
3 4
3 2
4 2
2 5

Output

2
1 4 

 

 

 题解：大概明白一个事情  原图中相连的两个点在补图中的连通性未知 但是不相连的两点在补图中一定属于同一联通块  这样的话 我们可以初始把所有的点全扔进一个链表中 从1-i开始对没有标记的点bfs 把没有相连且在链表中的点搜完 == 搜完补图中这个联通块的所有点  时间复杂度大概是(n+m) q巨讲解...但是对于复杂度的分析 我是直接类比 拓扑的复杂度分析...嗯  List或者手写链表 比vector快的多  可能我姿势不对吧

 

#include <bits/stdc++.h>
#define N 200005
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f*x;
}
list<int>vec;
list<int>::iterator ite;
bool vis[N];
vector<int>v_[N];
int ans[N];
queue<int>que;
bool cn[N];int n,m; 
void bfs(int t,int e){
	while(!que.empty()) que.pop();
	que.push(t);
	while(!que.empty()){
		int v=que.front();que.pop();
		if(vis[v]) continue;
		vis[v]=1;ans[e]++;
		for(int i=0;i<v_[v].size();i++) cn[v_[v][i]]=1;
		for(ite=vec.begin();ite!=vec.end();){
			int u=(*ite);
			if(!cn[u]){
				que.push(u);vec.erase(ite++);
			}
			else ite++;
		}
		for(int i=0;i<v_[v].size();i++) cn[v_[v][i]]=0;
	}
}
int main(){
	ios::sync_with_stdio(false);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) vec.push_back(i);
	int t1,t2;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&t1,&t2);
		v_[t1].push_back(t2);
		v_[t2].push_back(t1);
	}
	int cnt=0;
	for(int i=1;i<=n;i++){
		if(!vis[i]){
			cnt++;
			bfs(i,cnt);
		}
	}
	printf("%d\n",cnt);
	sort(ans+1,ans+cnt+1);
	for(int i=1;i<=cnt;i++){
		if(i==1) printf("%d",ans[i]);
		else printf(" %d",ans[i]);
	}
	printf("\n");
	return 0;
}

 

 F... 次场比赛败点  ....分析可知D函数 最多执行7次  也就是说一个点最多被更新7次  这个套路告诉我们了  你直接大胆让他更新到叶子节点 然后打一个最大值的标记 <=2  不执行更新即可 这样的话比打lazy快了不知道多少  很气的是  edu场的数据 弱的一批 被加入的数据 不修改查询的数据卡掉(不修改我的查询等价于每一个都跑到叶子节点->直接退化到n^2的算法....出题人太坏 自己太菜

F. SUM and REPLACE

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let D(x) be the number of positive divisors of a positive integer x. For example, D(2) = 2 (2 is divisible by 1 and 2), D(6) = 4 (6 is divisible by 1, 2, 3 and 6).

You are given an array a of n integers. You have to process two types of queries:

1. REPLACE l r — for every 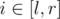replace a_i with D(a_i);
2. SUM l r — calculate .

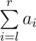Print the answer for each SUM query.

Input

The first line contains two integers n and m (1 ≤ n, m ≤ 3·10⁵) — the number of elements in the array and the number of queries to process, respectively.

The second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁶) — the elements of the array.

Then m lines follow, each containing 3 integers t_i, l_i, r_i denoting i-th query. If t_i = 1, then i-th query is REPLACE l_i r_i, otherwise it's SUM l_i r_i (1 ≤ t_i ≤ 2, 1 ≤ l_i ≤ r_i ≤ n).

There is at least one SUM query.

Output

For each SUM query print the answer to it.

Example

Input

7 6
6 4 1 10 3 2 4
2 1 7
2 4 5
1 3 5
2 4 4
1 5 7
2 1 7

Output

30
13
4
22

#include <bits/stdc++.h>
#define N 300005
#define M 1000001
#define ll long long
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f*x;
}
typedef struct node{
	int l,r,mx;
	ll sum;
}node;
node d[N<<2];
int dd[M];int a[N];
int n,m;
void up(int root){
	d[root].sum=d[root<<1].sum+d[root<<1|1].sum;
	d[root].mx=max(d[root<<1].mx,d[root<<1|1].mx);
}
void built(int root,int l,int r){
	if(l==r){
		d[root].l=d[root].r=l;d[root].mx=d[root].sum=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	built(root<<1,l,mid);
	built(root<<1|1,mid+1,r);
	d[root].l=d[root<<1].l;d[root].r=d[root<<1|1].r;
	up(root);
}
void update(int root,int l,int r){
	if(d[root].mx<=2) return ;
	if(d[root].l==d[root].r){
		d[root].mx=d[root].sum=dd[d[root].sum];
		return ;
	}
	int mid=(d[root].l+d[root].r)>>1;
	if(l<=mid) update(root<<1,l,r);
	if(r>mid) update(root<<1|1,l,r);
	up(root);
}
ll ans;
void querty(int root,int l,int r){
	if(l<=d[root].l&&d[root].r<=r){
		ans+=d[root].sum;
		return ;
	}
	int mid=(d[root].l+d[root].r)>>1;
	if(l<=mid) querty(root<<1,l,r);
	if(r>mid) querty(root<<1|1,l,r);
}
int main(){
	for(int i=1;i<M;i++){
		for(int j=1;j*i<M;j++){
			++dd[i*j];
		}
	}
	n=read();m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	built(1,1,n);
	int op,l,r;
	while(m--){
		op=read();l=read();r=read();
		if(op==1) update(1,l,r);
		else{
			ans=0;
			querty(1,l,r);
			printf("%lld\n",ans);
		}
	}
	return 0;
}

 G 大概是我认真补的第二道数论题-> 大概就是  要明白 小于p 且与一些因子互质的个数 等于这个数减去小于p且这些因子形成的数的个数  容斥一下 解决小于p且与因子互质的个数 然后很明显的是 随着p的增大这个个数是单调非递减的  而我们求第K大  也就是求第res(x)+k大 然后很明显的二分答案(大概1e9就可以得到所有答案

G. List Of Integers

time limit per test

5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's denote as L(x, p) an infinite sequence of integers y such that gcd(p, y) = 1 and y > x (where gcd is the greatest common divisor of two integer numbers), sorted in ascending order. The elements of L(x, p) are 1-indexed; for example, 9, 13 and 15 are the first, the second and the third elements of L(7, 22), respectively.

You have to process t queries. Each query is denoted by three integers x, p and k, and the answer to this query is k-th element of L(x, p).

Input

The first line contains one integer t (1 ≤ t ≤ 30000) — the number of queries to process.

Then t lines follow. i-th line contains three integers x, p and k for i-th query (1 ≤ x, p, k ≤ 10⁶).

Output

Print t integers, where i-th integer is the answer to i-th query.

Examples

Input

3
7 22 1
7 22 2
7 22 3

Output

9
13
15

Input

5
42 42 42
43 43 43
44 44 44
45 45 45
46 46 46

Output

187
87
139
128
141

#include <bits/stdc++.h>
#define ll long long
using namespace std;
vector<ll>vec;
ll res(ll x){
	ll ans=0;int n=vec.size();
	for(int i=0;i<(1<<n);i++){
		ll num=1;int tag=1;
		for(int j=0;j<n;j++){
			ll t=(i>>(j));
			if(t&1) num*=vec[j],tag*=-1;
		}
		ans+=(tag)*(x/num);
	}
	return ans;
} 
int main(){
	ios::sync_with_stdio(false);
	int T;scanf("%d",&T);ll x,p,k;
	while(T--){
		scanf("%lld%lld%lld",&x,&p,&k);
		for(ll i=2;i*i<=p;i++){
			if(p%i==0){
				vec.push_back(i);
				while((p%i)==0) p=p/i;
			}
		}
		if(p>1) vec.push_back(p);
		k+=res(x);
		ll l=1;ll r=1e9;ll ans;
		while(l<=r){
			ll mid=(l+r)>>1;
			if(res(mid)>=k){
				ans=mid;r=mid-1;
			}
			else l=mid+1;
		}
		printf("%I64d\n",ans);
		vec.clear();
	}
	return 0;
}