AP算法之python实现
AP算法简介
AP聚类一般翻译为近邻传播聚类,07年被提出,其优点有:
1. 不需要制定最终聚类族的个数
2. 已有的数据点作为最终的聚类中心,而不是新生成一个族中心。
3. 模型对数据的初始值不敏感。
4. 对初始相似度矩阵数据的对称性没有要求。
5. 相比与k-centers聚类方法,其结果的平方差误差较小。
它根据N个数据点之间的相似度进行聚类,这些相似度可以是对称的,即两个数据点互相之间的相似度一样(如欧氏距离);也可以是不对称的,即两个数据点互相之间的相似度不等。
这些相似度组成N×N的相似度矩阵S(其中N为有N个数据点)。
AP算法不需要事先指定聚类数目,相反它将所有的数据点都作为潜在的聚类中心,称之为 exemplar。
以S矩阵的对角线上的数值s (k, k)作为k点能否成为聚类中心的评判标准,这意味着该值越大,这个点成为聚类中心的可能性也就越大,这个值又称作参考度p ( preference) 。
聚类的数量受到参考度p的影响,如果认为每个数据点都有可能作为聚类中心,那么p就应取相同的值。如果取输入的相似度的均值作为p的值,得到聚类数量是中等的。如果取最小值,得到类数较少的聚类。
AP算法中传递两种类型的消息,(responsiility)和(availability) 。
r(i,k)表示从点i发送到候选聚类中心k的数值消息,反映k点是否适合作为i点的聚类中心。
a(i,k)则从候选聚类中心k发送到i的数值消息,反映i点是否选择k作为其聚类中心。
r (i, k)与a (i, k)越强,则k点作为聚类中心的可能性就越大,并且i点隶属于以k点为聚类中心的聚类的可能性也越大。
AP算法通过迭代过程不断更新每一个点的吸引度和归属度值,直到产生m个高质量的exemplar,同时将其余的数据点分配到相应的聚类中。
在这里介绍几个文中常出现的名词:
exemplar:指的是聚类中心。
similarity:数据点i和点j的相似度记为S(i,j)。是指点j作为点i的聚类中心的相似度。
preference:数据点i的参考度称为P(i)或S(i,i)。是指点i作为聚类中心的参考度。一般取S相似度值的中值。
Responsibility:R(i,k)用来描述点k适合作为数据点i的聚类中心的程度。
Availability:A(i,k)用来描述点i选择点k作为其聚类中心的适合程度。
Damping factor:阻尼系数,主要是起收敛作用的。
可以用一个比喻来理解这两个量和其之间交替过程:选举。
将聚类过程看成选举:
- 所有人都参加选举(大家都是选民也都是参选人),要选出几个作为代表
- s(i,k)就相当于i对选k这个人的一个固有的偏好程度
- r(i,k)表示用s(i,k)减去最强竞争者的评分,可以理解为k在对i这个选民的竞争中的优势程度
- r(i,k)的更新过程对应选民i的各个参选人的挑选(越出众越有吸引力)
- a(i,k):从公式里可以看到,所有r(i',k)>0的值都对a有正的加成。对应到我们这个比喻中,就相当于选民i通过网上关于k的民意调查看到:有很多人(即i'们)都觉得k不错(r(i',k)>0),那么选民i也就会相应地觉得k不错,是个可以相信的选择
- a(i,k)的更新过程对应关于参选人k的民意调查对于选民i的影响(已经有了很多跟随者的人更有吸引力)
- 两者交替的过程也就可以理解为选民在各个参选人之间不断地比较和不断地参考各个参选人给出的民意调查。
- r(i,k)的思想反映的是竞争,a(i,k)则是为了让聚类更成功。
整个算法的思想好像是基于置信传播(Belief Propagation)和对应的sum-product algorithm,可见wiki上对应词条和词条的参考文献。
AP聚类算法是将每个数据看成图中的一个节点,迭代的过程即是在图中通过传播信 息来找到聚类集合。
本文计算两个数据点的相似度采用距离的负数,也就是说距离越近,相似度越大。
相似矩阵S中i到j的相似度就是刚刚所说的距离的负数。但是主对角线上的那些数表示的是某个点和自身的相似度,但是这里我们不能直接用0来表示。根据算法要求,主对角线上的值s(k,k)一般称为偏向参数,一般 情况下对所有k,s(k,k)都相等,取非主对角线上的所有数的中位数。这个值很重要,他的大小与最后得到的类的数目有关,一般而言这个数越大,得到的类的数目就越多。
这里为什么要设定一个偏向参数而不直接用0来算呢,估计是因为AP聚类算法是要 用图论的一些东西来理解的,它把所有的点都看成一个图中的节点,通过节点之间的信息传递来达到聚类的效果。
聚类就是个不断迭代的过程,迭代的过程主要更新两个矩阵,代表(Responsibility)矩阵R = [r(i,k)]N×N和适选(Availabilities)矩阵A=[a(i,k)]N×N。这两个矩阵才初始化为0,N是所有样本的数目。
r(i,k)表示第k个样本适合作为第i个样本的类代表点的代表程度,a(i,k)表示第i个样本选择第k个样本作为类代表样本的适合程度。迭代更新公式如下:
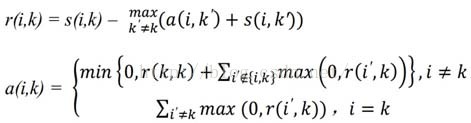
- s(i,j):数据点i与数据点j的相似度值,一般使用欧氏距离的的负值表示,即s(i,j)值越大表示点i与j的距离越近,AP算法中理解为数据点j作为数据点i的聚类中心的能力;
- 相似度矩阵:作为算法的初始化矩阵,n个点就有由n乘n个相似度值组成的矩阵;
- Preference参考度或称为偏好参数:是相似度矩阵中横轴纵轴索引相同的点,如s(i,i),若按欧氏距离计算其值应为0,但在AP聚类中其表示数据点i作为聚类中心的程度,因此不能为0。迭代开始前假设所有点成为聚类中心的能力相同,因此参考度一般设为相似度矩阵中所有值得最小值或者中位数,但是参考度越大则说明个数据点成为聚类中心的能力越强,则最终聚类中心的个数则越多;
- Responsibility,r(i,k):吸引度信息,表示数据点k适合作为数据点i的聚类中心的程度;
- 其中a(i,k’)表示除k外其他点对i点的归属度值,初始为0;s(i,k’)表示除k外其他点对i的吸引度,即i外其他点都在争夺i点的 所有权
- r(i,k)表示数据点k成为数据点i的聚类中心的累积证明,r(i,k)值大于0,则表示数据点k成为聚类中心的能力强。说明:此时只考虑哪个点k成为点i的聚类中心的可能性最大,但是没考虑这个吸引度最大的k是否也经常成为其他点的聚类中心(即归属度),若点k只是点i的聚类中心,不是其他任何点的聚类中心,则会造成最终聚类中心个数大于实际的中心个数。
- Availability,a(i,k):归属度信息,表示数据点i选择数据点k作为其聚类中心的合适程度;
- r(i’,k)表示点k作为除i外其他点的聚类中心的相似度值,取所有大于等于0的吸引度值,加上k作为聚类中心的可能程。即点k在这些吸引度值大于0的数据点的支持下,数据点i选择k作为其聚类中心的累积证明。
- Damping factor阻尼系数:为防止数据震荡,引入地衰减系数,每个信息值等于前一次迭代更新的信息值的λ倍加上此轮更新值得1-λ倍,其中λ在0-1之间,默认为0.5
每次更新后就可以确定当前样本i的代表样本(exemplar)点k,k就是使{a(i,k)+r(i,k)}取得最大值的那个k,如果i=k的话,那么说明样本i就是自己这个cluster的类代表点,如果不是,那么说明i属于k所属的那个cluster。
当然,迭代停止的条件就是所有的样本的所属都不在变化为止,或者迭代了n次都还没有变化(n的值可以自己取)。
说起来还有一种判断点属于属于哪一类的方法,就是找出所有决策矩阵主对角线元素{a(k,k)+r(k,k)}大于0的所有点,这些点全部都是类代表点,之后在决定其余的点属于这里面的一类。
另外还有一点就是AP聚类算法迭代过程很容易产生震荡,所以一般每次迭代都加上一个阻尼系数λ:
rnew(i,k) = λ*rold(i,k) + (1-λ)*r(i,k)
anew(i,k) = λ*aold(i,k) + (1-λ)*a(i,k)
代码实现:
1 # coding:utf-8 2 3 from sklearn.datasets.samples_generator import make_blobs 4 import matplotlib.pyplot as plt 5 import random 6 import numpy as np 7 8 ############################################################################## 9 # Generate sample data 10 centers = [[1, 1], [-1, -1], [1, -1]] 11 X, labels_true = make_blobs(n_samples=1000, centers=centers, cluster_std=0.4, 12 random_state=0) 13 14 ############################################################################## 15 16 17 def euclideanDistance(X, Y): 18 """计算每个点与其他所有点之间的欧几里德距离""" 19 X = np.array(X) 20 Y = np.array(Y) 21 # print X 22 return np.sqrt(np.sum((X - Y) ** 2)) 23 24 25 26 def computeSimilarity(datalist): 27 28 num = len(datalist) 29 30 Similarity = [] 31 for pointX in datalist: 32 dists = [] 33 for pointY in datalist: 34 dist = euclideanDistance(pointX, pointY) 35 if dist == 0: 36 dist = 1.5 37 dists.append(dist * -1) 38 Similarity.append(dists) 39 40 return Similarity 41 42 43 def affinityPropagation(Similarity, lamda): 44 45 #初始化 吸引矩阵 和 归属 矩阵 46 Responsibility = np.zeros_like(Similarity, dtype=np.int) 47 Availability = np.zeros_like(Similarity, dtype=np.int) 48 49 num = len(Responsibility) 50 51 count = 0 52 while count < 10: 53 count += 1 54 # update 吸引矩阵 55 56 for Index in range(num): 57 # print len(Similarity[Index]) 58 kSum = [s + a for s, a in zip(Similarity[Index], Availability[Index])] 59 # print kSum 60 for Kendex in range(num): 61 kfit = delete(kSum, Kendex) 62 # print fit 63 ResponsibilityNew = Similarity[Index][Kendex] - max(kfit) 64 Responsibility[Index][Kendex] = lamda * Responsibility[Index][Kendex] + (1 - lamda) * ResponsibilityNew 65 66 # print "Responsibility", Responsibility 67 68 69 # update 归属矩阵 70 71 ResponsibilityT = Responsibility.T 72 73 # print ResponsibilityT, Responsibility 74 75 for Index in range(num): 76 77 iSum = [r for r in ResponsibilityT[Index]] 78 79 for Kendex in range(num): 80 81 # print Kendex 82 # print "ddddddddddddddddddddddddddd", ResponsibilityT[Kendex] 83 # 84 ifit = delete(iSum, Kendex) 85 ifit = filter(isNonNegative, ifit) #上面 iSum 已经全部大于0 会导致 delete 下标错误 86 87 # k == K 对角线的情况 88 if Kendex == Index: 89 AvailabilityNew = sum(ifit) 90 else: 91 result = Responsibility[Kendex][Kendex] + sum(ifit) 92 AvailabilityNew = result if result > 0 else 0 93 Availability[Kendex][Index] = lamda * Availability[Kendex][Index] + (1 - lamda) * AvailabilityNew 94 print "###############################################" 95 print Responsibility 96 print Availability 97 print "###############################################" 98 return Responsibility + Availability 99 100 def computeCluster(fitable, data): 101 clusters = {} 102 num = len(fitable) 103 for node in range(num): 104 fit = list(fitable[node]) 105 key = fit.index(max(fit)) 106 if not clusters.has_key(key): 107 clusters[key] = [] 108 point = tuple(data[node]) 109 clusters[key].append(point) 110 111 return clusters 112 ############################################################################## 113 114 """切片删除 返回新数组""" 115 def delete(lt, index): 116 lt = lt[:index] + lt[index+1:] 117 return lt 118 119 def isNonNegative(x): 120 return x >= 0 121 122 123 ############################################################################## 124 125 Similarity = computeSimilarity(X) 126 127 Similarity = np.array(Similarity) 128 129 print "Similarity", Similarity 130 131 fitable = affinityPropagation(Similarity, 0.34) 132 133 print fitable 134 135 clusters = computeCluster(fitable, X) 136 137 # print clusters 138 139 ############################################################################## 140 clusters = clusters.values() 141 142 print len(clusters) 143 144 ############################################################################## 145 def plotClusters(clusters, title): 146 """ 画图 """ 147 plt.figure(figsize=(8, 5), dpi=80) 148 axes = plt.subplot(111) 149 col=[] 150 r = lambda: random.randint(0,255) 151 for index in range(len(clusters)): 152 col.append(('#%02X%02X%02X' % (r(),r(),r()))) 153 color = 0 154 for cluster in clusters: 155 cluster = np.array(cluster).T 156 axes.scatter(cluster[0],cluster[1], s=20, c = col[color]) 157 color += 1 158 plt.title(title) 159 # plt.show() 160 ############################################################################## 161 plotClusters(clusters, "clusters by affinity propagation") 162 plt.show() 163 164 ##############################################################################
本文来自于:
kael : AP算法中两个参数的交替过程怎么样通俗的理解?
winkake : Affinity Propagation: AP聚类算法
Mrchesian : python 实现 AP近邻传播聚类算法(Affinity Propagation)
谢谢作者!!!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号