BatchNormalization、LayerNormalization、InstanceNormalization和GroupNormalization四者的比较
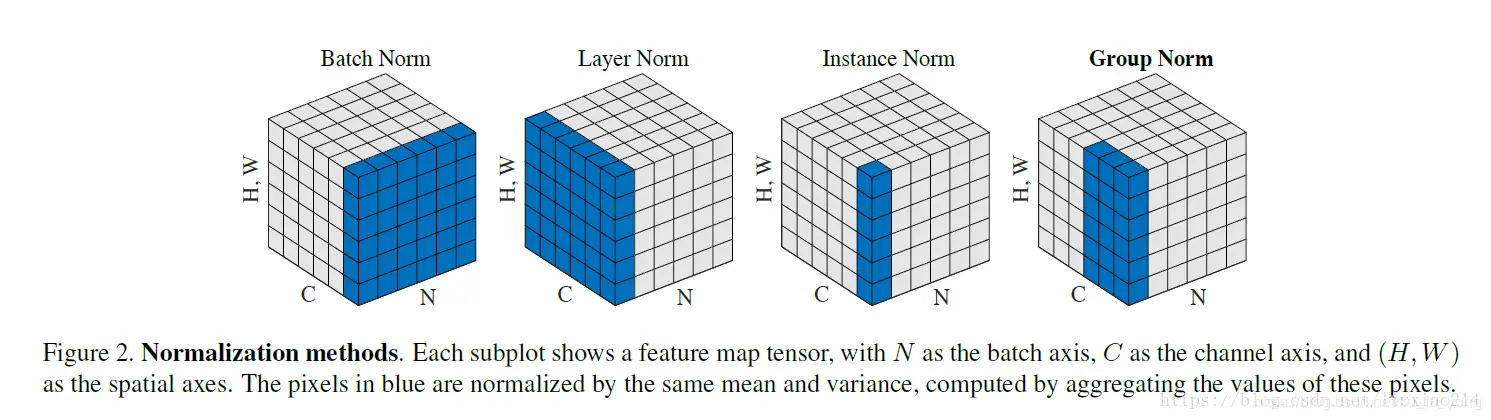
从公式看它们都差不多:无非是减去均值,除以标准差,再施以线性映射:
$y = \gamma (\frac{x-\mu (x)}{\sigma (x)}) + \beta$
这些归一化算法的主要区别在于操作的 feature map 维度不同。
Batch Normalization
如果把 $x \in R ^{N\times C\times H\times W}$ 类比为一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 W 个字符。BN 求均值时,相当于把这些书按页码一一对应地加起来(例如第1本书第36页,第2本书第36页......),再除以每个页码下的字符总数:N×H×W,因此可以把 BN 看成求“平均书”的操作(注意这个“平均书”每页只有一个字),求标准差时也是同理。
Layer Normalization
BN 的一个缺点是需要较大的 batchsize 才能合理估训练数据的均值和方差,这导致内存很可能不够用,同时它也很难应用在训练数据长度不同的 RNN 模型上。Layer Normalization (LN) 的一个优势是不需要批训练,在单条数据内部就能归一化。
对于 $x \in R ^{N\times C\times H\times W}$ ,LN 对每个样本的 C、H、W 维度上的数据求均值和标准差,保留 N 维度。其均值和标准差公式为:
Instance Normalization
Instance Normalization (IN) 最初用于图像的风格迁移。作者发现,在生成模型中, feature map 的各个 channel 的均值和方差会影响到最终生成图像的风格,因此可以先把图像在 channel 层面归一化,然后再用目标风格图片对应 channel 的均值和标准差“去归一化”,以期获得目标图片的风格。IN 操作也在单个样本内部进行,不依赖 batch。
对于 $x \in R ^{N\times C\times H\times W}$ ,IN 对每个样本的 H、W 维度的数据求均值和标准差,保留 N 、C 维度,也就是说,它只在 channel 内部求均值和标准差,其公式为:
IN 求均值时,相当于把一页书中所有字加起来,再除以该页的总字数:H×W,即求每页书的“平均字”,求标准差时也是同理。
Group Normalization
Group Normalization (GN) 适用于占用显存比较大的任务,例如图像分割。对这类任务,可能 batchsize 只能是个位数,再大显存就不够用了。而当 batchsize 是个位数时,BN 的表现很差,因为没办法通过几个样本的数据量,来近似总体的均值和标准差。GN 也是独立于 batch 的,它是 LN 和 IN 的折中。
GN 计算均值和标准差时,把每一个样本 feature map 的 channel 分成 G 组,每组将有 C/G 个 channel,然后将这些 channel 中的元素求均值和标准差。各组 channel 用其对应的归一化参数独立地归一化。
比较
1、Weight Normalization与Batch Normalization对比
Weight Normalization和Batch Normalization都属于参数重写(Reparameterization)的方法,只是采用的方式不同,Weight Normalization是对网络权值W进行normalization(L2 norm),因此也称为Weight Normalization;Batch Normalization是对网络某一层输入数据进行normalization。
Weight Normalization相比Batch Normalization有以下三点优势:
- Weight Normalization通过重写深度学习网络的权重W的方式来加速深度学习网络参数收敛,没有引入minbatch的依赖,适用于RNN(LSTM)网络(Batch Normalization不能直接用于RNN,进行normalization操作,原因在于:1、RNN处理的Sequence是变长的;2、RNN是基于time step计算,如果直接使用Batch Normalization处理,需要保存每个time step下,mini btach的均值和方差,效率低且占内存)。
- Batch Normalization基于一个mini batch的数据计算均值和方差,而不是基于整个Training set来做,相当于进行梯度计算式引入噪声。因此,Batch Normalization不适用于对噪声敏感的强化学习、生成模型(Generative model:GAN,VAE)使用。相反,Weight Normalization对通过标量g和向量v对权重W进行重写,重写向量v是固定的,因此,基于Weight Normalization的Normalization可以看做比Batch Normalization引入更少的噪声。
- 不需要额外的存储空间来保存mini batch的均值和方差,同时实现Weight Normalization时,对深度学习网络进行正向信号传播和反向梯度计算带来的额外计算开销也很小。因此,要比采用Batch Normalization进行normalization操作时,速度快。 但是, Weight Normalization不具备Batch Normalization把网络每一层的输出Y固定在一个变化范围的作用。因此,采用Weight Normalization进行Normalization时需要特别注意参数初始值的选择。
2、Layer Normalization与Batch Normalization对比:
BN针对一个minibatch的输入样本,计算均值和方差,基于计算的均值和方差来对某一层神经网络的输入X中每一个case进行归一化操作。
但BN有两个明显不足:
1、高度依赖于mini-batch的大小,实际使用中会对mini-Batch大小进行约束,不适合类似在线学习(mini-batch为1)情况;
2、不适用于RNN网络中normalize操作:BN实际使用时需要计算并且保存某一层神经网络mini-batch的均值和方差等统计信息,对于对一个固定深度的前向神经网络(DNN,CNN)使用BN,很方便;但对于RNN来说,sequence的长度是不一致的,换句话说RNN的深度不是固定的,不同的time-step需要保存不同的statics特征,可能存在一个特殊sequence比其的sequence长很多,这样training时,计算很麻烦。但LN可以有效解决上面这两个问题。 LN适用于LSTM的加速,但用于CNN加速时并没有取得比BN更好的效果。
总结
这里再重复一下上文的类比。如果把 $x \in R ^{N\times C\times H\times W}$ 类比为一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 W 个字符。
计算均值时
- BN 相当于把这些书按页码一一对应地加起来(例如:第1本书第36页,加第2本书第36页......),再除以每个页码下的字符总数:N×H×W,因此可以把 BN 看成求“平均书”的操作(注意这个“平均书”每页只有一个字)
- LN 相当于把每一本书的所有字加起来,再除以这本书的字符总数:C×H×W,即求整本书的“平均字”
- IN 相当于把一页书中所有字加起来,再除以该页的总字数:H×W,即求每页书的“平均字”
- GN 相当于把一本 C 页的书平均分成 G 份,每份成为有 C/G 页的小册子,对这个 C/G 页的小册子,求每个小册子的“平均字”
计算方差同理
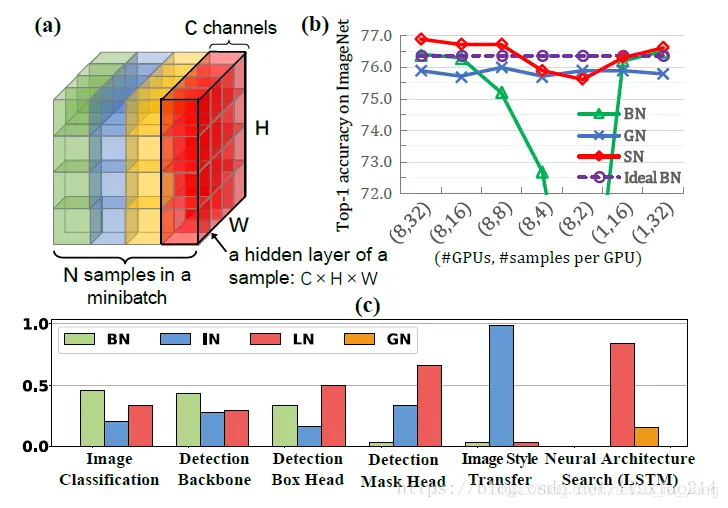
本文来源于:
瞎了吗:BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm、SwitchableNorm简介
lafarmer: 深度学习加速策略BN、WN和LN的联系与区别,各自的优缺点和适用的场景?
Juliuszh:详解深度学习中的Normalization,不只是BN
感谢作者!!!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号