数论1-素数

Part 1 前置

记号约定

整数集合：$ \Z ={...,-2,-1,0,1,2,…}$
自然数集合：$\N=\{0,1,2,…\}$, 下文若不特殊说明，则出现的所有字母皆代表自然数。
整除：若 $a=b\times k$, 则 $b$ 整除 $a$, 记作 $b \mid a$, 否则记作 $b \nmid a$
约数：若 $b\mid a$ 且 $b\ge 0$,则称 $b$ 是 $a$ 的约数，$a$ 是 $b$ 的倍数。约数有一些性质，这里按下不表。
因子：$a$ 除了 $1$ 和 $a$ 本身以外的所有约数称为 $a$ 的因子。（这里为了方便，就直接这么写了）

何为数论

研究整数性质的数学分支，本质上是对质数（素数）的研究。

Part 2: 素数的一切

若不加额外说明，下文中 $p$ 皆表示质数，$m$ 表示非质数且 $m>1$。

定义

素数（质数）：$p>1$ 且没有因子的数。
合数：$m>1$ 且有因子的数。
其他整数（0,1）既不是质数也不是合数。
- 素数的分布规律：不大于 $n$ 的素数约有 $\frac{n}{\ln{n}}$ 个。

判断

#1

若 $m$ 不是质数，则它一定有至少一个素因子，这些素因子一定不会大于 $\sqrt{m}$ 。

那么只要从 $2$ 枚举到 $\sqrt{m}$ 判断能否整除即可。

时间复杂度单次 $\mathcal O(\sqrt{m})$。

Code:

bool isprime(int m){
    if(m<2)return false;
    for(int i=2;i*i<=m;i++)
        if(m%i==0)return false;
   	return true;
}

#2 $kn+i$ 法

最近学到的一个黑科技。我们枚举时并不需要把所有数都看一遍。$m$ 如果不是质数，那么它一定有素因子。我们枚举时只需要枚举可能为素因子的数即可。

比如当 $k=6$ 时，我们只需要枚举 $kn+1$ 和 $kn+5$ 即可，其他数不可能为质数。

时间复杂度仍为单次 $\mathcal O(\sqrt{m})$，但是常数小了好多。

Code:(此处 $k=30$)

bool isprime(int m){
    if(m==2||m==3||m==5)return true;
    if(m%2==0||m%3==0||m%5==0||m==1)return 0;
    int c=7,a[8]={4,2,4,2,4,6,2,6};
    while(c*c<n){
        for(auto i:a){
            if(n%c==0)return 0;
        	c+=i;
        }
    }
    return 1;
}

#3 预处理

对于多组数据，每个 $m$ 必然有小于等于 $\sqrt{m}$ 的素因子，只需要对 $\sqrt{m}$ 内的素数测试即可。

我们可以预处理出 $\sqrt{m}$ 内的素数，再让每一个 $m$ 对这些素数进行测试。

时间复杂度近似单次 $\mathcal O(\frac{m}{\ln{m}})$。

预处理详见下章，代码不贴了。

#4 Miller_Rabin

最重要。

前置知识-费马小定理

若 $p$ 是质数，且 $a$ 与 $p$ 互素，则 $a^{p-1}\equiv 1 \pmod p$ 。

证明：

$p-1$ 个整数 $a,2a,3a,...,(p-1)a$，其中没有一个是 $p$ 的倍数，且没有任意两个模 $p$ 同余。
所以这些数模 $p$ 的余数是 $1,2,3,…,(p-1)$ 的排列。
于是得 $a\times 2a \times 3a \times … \times (p-1)a \equiv 1 \times 2 \times ... \times (p-1) \pmod{p}$
可化简为 $a^{p-1} \times (p-1)! \equiv (p-1)! \pmod p$
于是原命题得证。

那么据此我们就可以得到它的逆否命题：若 $a^{m-1}\not\equiv 1 \pmod{m}$ , 则 $m$ 不是质数。

但是这个命题不一定是正确的！事实上，对于伪素数（一种特殊的合数）中的卡迈克尔数，你就算把从 $1$ 到那个数的所有质数都算一遍仍然是有问题的。那么就引出了我们的第二个引理——

前置知识-二次探测定理

对于一个奇质数 $p$ (只有 $2$ 不是奇质数)，则 $x^2\equiv 1 \pmod p$ 的解为 $x\equiv 1 \pmod{p}$ 或 $x\equiv p-1 \pmod{p}$。

证明：

由 $x^2\equiv 1 \pmod p$ 得 $x^2-1\equiv 0 \pmod p$
即 $(x+1)(x-1)\equiv 0 \pmod p$
即 $x+1 \equiv 0 \pmod p$ 或 $x-1\equiv 0 \pmod p$
即 $x \equiv p-1 \pmod p$ 或 $x \equiv 1 \pmod p$

知道了这些之后我们就可以愉快的进行判定了！

具体步骤

我们假定要判定的数 $m$ 是一个奇素数，令 $s=m-1$，那么$s$ 一定是偶数，可以分解成 $s=2^k\times b$ 的形式。

我们首先根据费马小定理的“逆命题”，判断 $m^{s}\equiv 1 \pmod m$ , 如果是那么我们就假定它是素数。

如果不是，根据二次探测定理，我们有

\[m^{s}\equiv s \pmod m\\ (m^{s})^2\equiv s \pmod m\\ {(m^{s})^2}^2\equiv s \pmod m\\ ...\\ {(m^{s})^2}^{b-1}\equiv s \pmod m \]

于是只要对系数不断平方直到：

如果有一个式子成立，我们就暂且认为判定为素数，返回。
如果每一个都不成立，我们就认为判定为合数，返回。

但是这不是一个确定性算法，也就是意味着这可能会判定失误。

所以我们需要选择多个和 $m$ 互素的数进行判定，一般选 $7$ 到 $10$ 个，如果都给出素数结果，那么这个数一般就是素数。

时间复杂度 $\mathcal O(k \log m)$，$k$ 为选择数的个数。

Code:

bool Miller_Rabin(int a,int n){
    int s=n-1,r=0;
    while(!(s&1)){s>>=1;r++;}
    long long k=qpow(a,s,n);
    if(k==1)return true;
    for(int i=0;i<r;i++,k=k*k%n/*可能溢出，用龟速乘*/){
		if(k==n-1)return true;        
    }
    return false;
}
bool isprime(int n){
    int times=8;
    int prime[100]={2,3,5,7,11,13,233,331};
    for(int i=0;i<times;i++){
        if(n==prime[i])return true;
        if(Miller_Rabin(prime[i],n)==false)return false;
    }
    return true;
}

例题

POJ-2089 Prime Distance

Link

题意：求区间 $[l,r]$ 范围内距离最大、最小的两个素数。（ $0\leq l < r \le 2.1\times 10^9 $ 且 $r-l\leq 10^6$ ）

题解：可以用 #3 的方法筛出 $\sqrt{2.1\times 10^9}$ 内的素数，也可以用 Miller_Rabin。

Code:

#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
int n;
#define int long long
#define ll long long
int a[1000010],b[10000010],p[100010];
int cnt=0,l,r; 
void prime(int n){//线性筛
	cnt=0;
	b[1]=1;
	for(int i=2;i<=n;i++){
		if(!b[i]){
			p[++cnt]=i;
			for(int j=1;p[j]*i<=n;j++){b[p[j]*i]=1;if(i%p[j]==0)break;}
		}
	}
}
signed main(){	
	prime(50505);
	while(cin>>l>>r){
		int res=0,lst=0;int maxl=0,maxr=0,minl=-114514,minr=1919810;
		memset(a,0,sizeof a);
		for(int i=1;i<=cnt;i++){
			int pr=p[i];
			for(int j=max(pr*2,(l+pr-1)/pr*pr);j<=r;j+=pr)a[j-l]=1;
		}
		for(ll i=l;i<=r;i++){
			if(!a[i-l]&&i!=1){res++;
				if(res>=2){
					if(maxr-maxl<i-lst){maxr=i,maxl=lst;}
					if(minr-minl>i-lst){minr=i,minl=lst;}
				}
				lst=i;	
			}
		}
		if(res<2){cout<<"There are no adjacent primes."<<endl;}
		else{cout<<minl<<","<<minr<<" are closest, "<<maxl<<","<<maxr<<" are most distant."<<endl;}
	}
	return 0;
}

筛法

前置—质因数分解

把一个合数分解为几个素因数的乘积。

我们有唯一分解定理：若整数 $n\ge 2$ ,那么 $n$ 一定可以唯一的表示为若干素数的乘积，形如

\[n=p_1^{r_1}p_2^{r_2}...p_k^{r_k}(p_i\text{为素数},r_i>0) \]

时间复杂度 $\mathcal O(\log n)$。

Code:

vector<int> factor(int x){
    vector<int>ret;
    for(int i=2;i*i<=x;i++){
        while(x%i==0){ret.push_back(i);x/=i;}
        if(x==1)break;
    }
    if(x>1)ret.push_back(x);//素数
    return ret;
}

埃氏筛

全名：埃拉托斯特尼筛法。

首先我们知道质数的倍数一定是合数（这里的倍数不包括它本身）。

并且一个数的因子一定小于它（狭义的因子，定义见上）。

于是我们对于每一个素数都把它所有的倍数筛掉（一定是合数），那么遍历到它时没被筛掉的就一定是质数，拿它再做筛选。

如图:

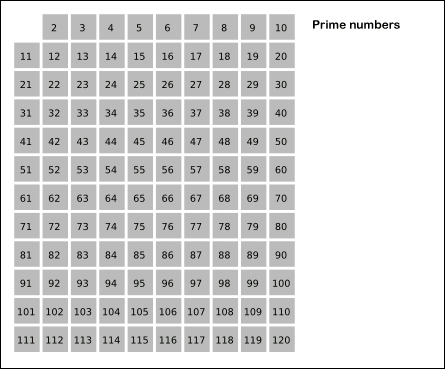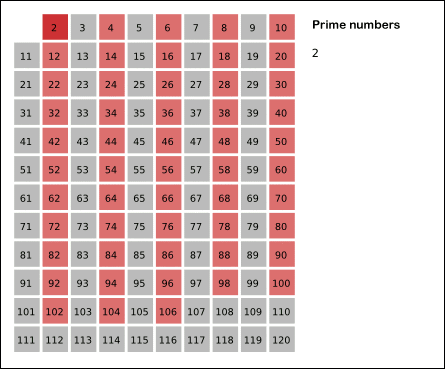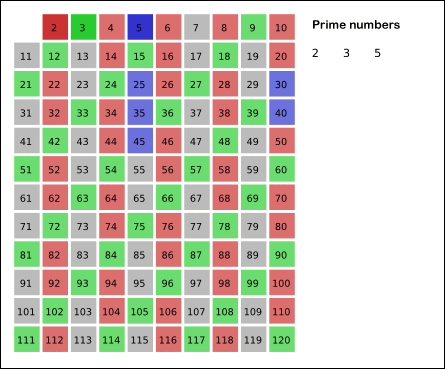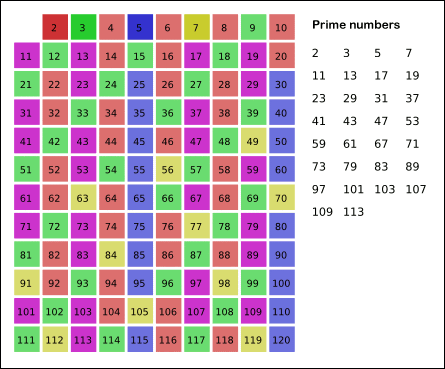
比较有意思的是它的复杂度。

我们首先看一个问题：

$\mathcal O(\sum_{i=1}^n \frac{1}{i})$ 是多少？

答案：(link)

\[\begin{aligned} \mathcal O(\sum_{i=1}^n \frac{1}{i})&=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}...+\frac{1}{n}\\ &= \frac{1}{1}+(\frac{1}{2}+\frac{1}{3})+(\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7})+...+\frac{1}{n}\\ &\le 1+(\frac{1}{2}+\frac{1}{2})+(\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4})+...+\frac{1}{n}\\ &= 1+1+1+...+1\\ &= \log_2 n \end{aligned} \]

然而我们只需要对于每一个质数进行操作。 $[1,n]$ 范围内的质数约有 $\log_2 n$ 个，加上遍历的复杂度，总复杂度为 $\mathcal O(n \log \log n)$。

Code:

bitset<1000010>b;
int prime[100010],cnt=0;
void prime(int n){
    for(int i=2;i<=n;i++)b[i]=0;
    for(int i=2;i<=n;i++){
        if(!b[i]){
            prime[++cnt]=i;
            for(int j=(long long)i*i;j<=n;j+=i)b[j]=1;
        }
    }
}

一些神秘的应用：质因数分解

我们可以在埃氏筛过程中记录每个合数的最小质因子，然后递归求解。

时间复杂度 $\mathcal O(\log n)$。

Code:

bitset<1000010>b;
int prime[100010],cnt=0;
int g[1000010];
void Eratos_prime(int n){
    for(int i=2;i<=n;i++)b[i]=0;
    for(int i=2;i<=n;i++){
        if(!b[i]){
            prime[++cnt]=i;g[i]=i;
            for(int j=(long long)i*i;j<=n;j+=i){
                if(!b[j]){b[j]=1;g[j]=i;}
            }
        }
    }
}
vector<int> factor(int x){
   Eratos_prime(x);vector<int>ret;
   while(x!=1){
       ret.push_back(g[x]);
       x/=g[x];
   }
   // if(x>1)ret.push_back(x);//素数
    return ret;
}

线性筛

又名：欧拉筛。

如果每个合数只被它的最小素因数筛除，那么每个数最多只筛一次。

具体步骤：

枚举 $[2,n]$ 中的每一个整数 $i$：
如果 $i$ 是素数就保存在素数表中；
利用 $i$ 和素数表中的素数 $p_j$ 去筛除 $i\times p_j$ ，为了确保 $i\times p_j$ 只被 $p_j$ 筛过一次，要确保 $p_j$ 是 $i\times p_j$ 中最小的质因子，即 $i$ 中不能有比 $p_j$ 还小的素因子。

参考：(篇幅所限，只写了 $[2,10]$筛 $[1,50]$ )

遍历的 $i$	筛除的 $i\times p_j$
$2$	$\{4\}$
$3$	$\{6,9\}$
$4$	$\{8,12\}$
$5$	$\{10,15,25\}$
$6$	$\{12,18\}$
$7$	$\{14,21,35,49\}$
$8$	$\{16\}$
$9$	$\{18,27\}$
$10$	$\{20\}$

时间复杂度 $\mathcal O(n)$。

代码：

bitset<1000010>b;
int prime[100010],cnt=0;
void Prime(int n){
    for(int i=2;i<=n;i++){
        if(!b[i])prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<=n;j++){
            b[i*prime[j]]=1;
            if(i%prime[j]==0)break;
        }
    }
}

posted @ 2024-01-29 19:47 wangyishan 阅读(27) 评论(0) 编辑收藏举报

刷新页面返回顶部

遍历的 \(i\)	筛除的 \(i\times p_j\)
\(2\)	\(\{4\}\)
\(3\)	\(\{6,9\}\)
\(4\)	\(\{8,12\}\)
\(5\)	\(\{10,15,25\}\)
\(6\)	\(\{12,18\}\)
\(7\)	\(\{14,21,35,49\}\)
\(8\)	\(\{16\}\)
\(9\)	\(\{18,27\}\)
\(10\)	\(\{20\}\)

一个愚公的笔记

--by Wangyishan

数论1-素数

Part 1 前置

记号约定

何为数论

Part 2: 素数的一切

定义

判断

#1

#2 \(kn+i\) 法

#3 预处理

#4 Miller_Rabin

前置知识-费马小定理

前置知识-二次探测定理

具体步骤

例题

POJ-2089 Prime Distance

筛法

前置—质因数分解

埃氏筛

一些神秘的应用：质因数分解

线性筛

公告