01笔记-树状数组学习笔记

01笔记-树状数组学习笔记

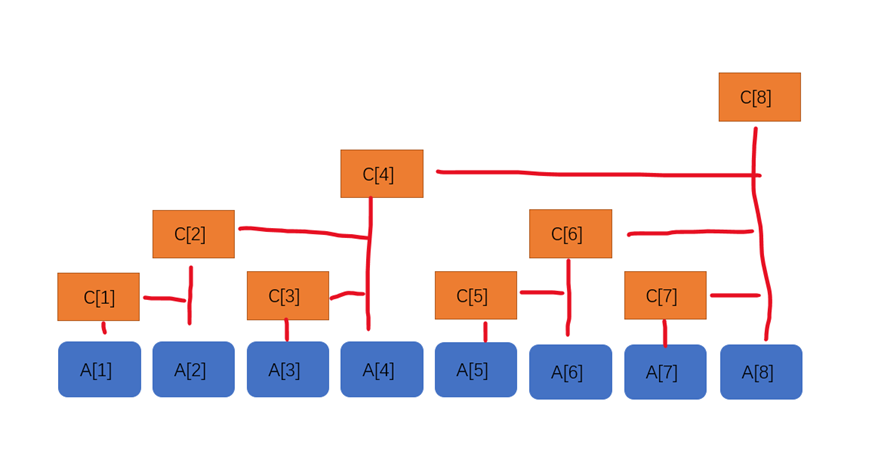
树状数组，顾名思义，就是“树状的”数组。树状数组支持以下操作：

1. 单点修改、区间求和
2. 区间修改、单点查询
3. 区间修改、区间查询

这三种操作都是 \(\Theta(logn)\) 的。

树状数组与线段树相比，更好写，但是线段树功能更强大。

树状数组主要依靠 \(lowbit\) ,这是一种求二进制意义下最后一个 \(1\) 所表示的数的位运算，写起来非常简单：设 \(x\) 为我们要求 \(lowbit\) 的未知数，则 \(lowbit(x)=x\&-x\)

例: \(lowbit(6)=lowbit(0101_2)=0101_2\&1011_2=10_2=2\)

树状数组需要定义一个辅助数组 \({c_i}\)，用于存储原数组 \(((a_{i-lowbit(i)+1})+(a_{i-lowbit(i)+2})+...+a_i)\) 的和。

代码1 题目：

#include <iostream>
using namespace std;
int n, m;
// int a[100010];
int C[500010];
#define lowbit(x) x & (-x)
void add(int x, int k)//给位置 x 加上 k，这里是递增加的（即从这棵‘树’的叶子结点往上加的）
{
    while (x <= n){
        C[x] += k;
        x += lowbit(x);
}
}
int getsum(int x)//获取从1到x的元素和，这里是递减加的
{
    int res = 0;
    while (x){
        res += C[x];
        x -= lowbit(x);
    }
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    cin >> n >> m;
    int t;
    for (int i = 1; i <= n; i++){
        cin >> t;
        add(i, t);
    }
    for (int i = 1; i <= m; i++){
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1){
            add(x, y);
        }
        else{
            cout << getsum(y) - getsum(x - 1) << endl;
        }
    }
    return 0;
}

---

对于2，我们考虑差分(注：差分是前缀和的逆运算，比如我想要给数组 \(a\) 的 \([l,r]\) 中加上 \(k\) ,我们就可以定义一个新数组 \(s\) , 把 \(s_l+k,s_{r+1}-k\), 此时我们 $a_m=a_m+\sum_{i=0}^{m} s_i $)。我们要优化的就是这个求和的过程。

我们首先把 \(c\) 数组全部初始化为 \(0\)，然后在每次区间 \([l,r]\) 加上 \(x\),就把 \(c_l+x , c_{r+1}-x\) , 在查询时查找 \(c_1+c_2+... + c_x\) 的和就可以了。

代码2 题目：

#include <iostream>
#include <cstdio>
using namespace std;
int n,m;
int C[500010],a[500010];
inline int lowbit(int x){
    return x&(-x);
}
void add(int x,int k){
    while(x<=n){
        C[x]+=k;
        x+=lowbit(x);
    }
}
int getsum(int x){
    int res=0;
    while(x){
        res+=C[x];
        x-=lowbit(x);
    }
    return res;
}
int main() {
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=m;i++){
        int op;
        cin>>op;
        if(op==1){
            int x,y,k;
            cin>>x>>y>>k;
            add(x,k);//差分
            add(y+1,-k);//差分
        }
        else{
            int x;
            cin>>x;
            cout<<a[x]+getsum(x)<<endl;
        }
    }
    return 0;
}

---

对于3，这里我引用了一位大佬@胡小兔 的说明：

代码 题目:

//这里我为了方便
//把1号的+-都认为是进行了一个[1,1]的区间修改
#include<iostream>
using namespace std;
#define lowbit(x) x&(-x)
long long c1[200010],c2[200010],a[200010];
long long n, f;
void add(long long y, long long k)
{
    int x=y;
    while(x<=n){
        c1[x]+=k;
        c2[x]+=k*y;
        x+=lowbit(x);
    }
}
long long getsum(long long y)
{
    long long res = 0;
    long long x = y;
    while(x){
        res+=(y+1)*c1[x]-c2[x];
        x-=lowbit(x);
    }
    return res;
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>f;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        add(i, a[i]);
        add(i+1, -a[i]);
    }
    for(int i=1;i<=f;i++){
        long long op, l, r, k;
        cin>>op;
        if(op==1){
            cin>>l>>r>>k;
            add(l,k);
            add(r+1,-k);
        }
        else if(op==2){
            cin>>k;
            add(1,k);
            add(2,-k);
        }
        else if(op==3){
            cin>>k;
            add(1,-k);
            add(2,k);
        }
        else if(op==4){
            cin>>l>>r;
            cout<<getsum(r)-getsum(l-1)<<endl;
        }
        else if(op==5){
            cout<<getsum(1)<<endl;
        }
    }
    return 0;
}